
In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends.

A sphere is a geometrical object in three-dimensional space that is the surface of a ball.
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved in some particular way, such as by lacking differentiability or analyticity.

In mathematics, a cubic function is a function of the form

A catenoid is a type of surface, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.

In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.

In mathematical analysis, the maxima and minima of a function, known collectively as extrema, are the largest and smallest value of the function, either within a given range, or on the entire domain. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions.

A surface of revolution is a surface in Euclidean space created by rotating a curve around an axis of rotation.

The helicoid, after the plane and the catenoid, is the third minimal surface to be known.

A tractrix is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a tractor (pulling) point that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1692).

Critical point is a wide term used in many branches of mathematics.

Three-dimensional space is a geometric setting in which three values are required to determine the position of an element. This is the informal meaning of the term dimension.

In mathematics, a crunode (archaic) or node is a point where a curve intersects itself so that both branches of the curve have distinct tangent lines at the point of intersection. A crunode is also known as an ordinary double point.

In mathematics, a Scherk surface is an example of a minimal surface. Scherk described two complete embedded minimal surfaces in 1834; his first surface is a doubly periodic surface, his second surface is singly periodic. They were the third non-trivial examples of minimal surfaces. The two surfaces are conjugates of each other.
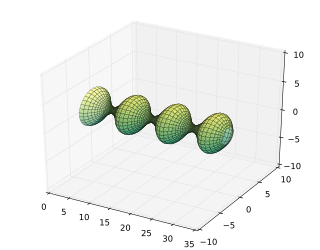
In geometry, an unduloid, or onduloid, is a surface with constant nonzero mean curvature obtained as a surface of revolution of an elliptic catenary: that is, by rolling an ellipse along a fixed line, tracing the focus, and revolving the resulting curve around the line. In 1841 Delaunay proved that the only surfaces of revolution with constant mean curvature were the surfaces obtained by rotating the roulettes of the conics. These are the plane, cylinder, sphere, the catenoid, the unduloid and nodoid.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.

In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as S1 because it is a one-dimensional unit n-sphere.
Carl Wolfgang Benjamin Goldschmidt was a German astronomer, mathematician, and physicist of Jewish descent who was a professor of astronomy at the University of Göttingen. He is also known as Benjamin Goldschmidt, C. W. B. Goldschmidt, Carl Goldschmidt, and Karl Goldschmidt.

In mathematics, Bour's minimal surface is a two-dimensional minimal surface, embedded with self-crossings into three-dimensional Euclidean space. It is named after Edmond Bour, whose work on minimal surfaces won him the 1861 mathematics prize of the French Academy of Sciences.
























