Nearest neighbor graph

Last updated
A nearest neighbor graph of 100 points in the Euclidean plane. Nearest neighbor graph.svg
A nearest neighbor graph of 100 points in the Euclidean plane.

The nearest neighbor graph (NNG) is a directed graph defined for a set of points in a metric space, such as the Euclidean distance in the plane. The NNG has a vertex for each point, and a directed edge from p to q whenever q is a nearest neighbor of p, a point whose distance from p is minimum among all the given points other than p itself. [1]

Contents

In many uses of these graphs, the directions of the edges are ignored and the NNG is defined instead as an undirected graph. However, the nearest neighbor relation is not a symmetric one, i.e., p from the definition is not necessarily a nearest neighbor for q. In theoretical discussions of algorithms a kind of general position is often assumed, namely, the nearest (k-nearest) neighbor is unique for each object. In implementations of the algorithms it is necessary to bear in mind that this is not always the case. For situations in which it is necessary to make the nearest neighbor for each object unique, the set P may be indexed and in the case of a tie the object with, e.g., the largest index may be taken as the nearest neighbor. [2]

The k-nearest neighbor graph (k-NNG) is a graph in which two vertices p and q are connected by an edge, if the distance between p and q is among the k-th smallest distances from p to other objects from P. The NNG is a special case of the k-NNG, namely it is the 1-NNG. k-NNGs obey a separator theorem: they can be partitioned into two subgraphs of at most n(d + 1)/(d + 2) vertices each by the removal of O(k1/dn1 − 1/d) points. [3] A k-NNG can be approximated using an efficient algorithm with 90% recall that is faster than a brute-force search by an order of magnitude. [4]


Another variation is the farthest neighbor graph (FNG), in which each point is connected by an edge to the farthest point from it, instead of the nearest point.

NNGs for points in the plane as well as in multidimensional spaces find applications, e.g., in data compression, motion planning, and facilities location. In statistical analysis, the nearest-neighbor chain algorithm based on following paths in this graph can be used to find hierarchical clusterings quickly. Nearest neighbor graphs are also a subject of computational geometry.

The method can be used to induce a graph on nodes with unknown connectivity.

NNGs for sets of points

One-dimensional case

For a set of points on a line, the nearest neighbor of a point is its left or right (or both) neighbor, if they are sorted along the line. Therefore, the NNG is a path or a forest of several paths and may be constructed in O(n log n) time by sorting. This estimate is asymptotically optimal for certain models of computation, because the constructed NNG gives the answer to the element uniqueness problem: it is sufficient to check whether the NNG has a zero-length edge. [5]

Higher dimensions

Unless stated otherwise, it is assumed that the NNGs are digraphs with uniquely defined nearest neighbors as described in the introduction.

  1. Along any directed path in an NNG the edge lengths are non-increasing. [2]
  2. Only cycles of length 2 are possible in an NNG and each weakly connected component of an NNG with at least 2 vertices has exactly one 2-cycle. [2]
  3. For the points in the plane the NNG is a planar graph with vertex degrees at most 6. If points are in general position, the degree is at most 5. [2]
  4. The NNG (treated as an undirected graph with multiple nearest neighbors allowed) of a set of points in the plane or any higher dimension is a subgraph of the Delaunay triangulation, the Gabriel graph, and the Semi-Yao graph. [6] If the points are in general position or if the single nearest neighbor condition is imposed, the NNG is a forest, a subgraph of the Euclidean minimum spanning tree.

Related Research Articles

<span class="mw-page-title-main">Delaunay triangulation</span> Triangulation method

In mathematics and computational geometry, a Delaunay triangulation (DT), also known as a Delone triangulation, for a given set {pi} of discrete points pi in general position is a triangulation such that no point pi is inside the circumcircle of any triangle in the DT. Delaunay triangulations maximize the minimum of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.

<span class="mw-page-title-main">Graph theory</span> Area of discrete mathematics

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.

<span class="mw-page-title-main">Component (graph theory)</span> Maximal subgraph whose vertices can reach each other

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

<span class="mw-page-title-main">Graph (discrete mathematics)</span> Vertices connected in pairs by edges

In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.

<span class="mw-page-title-main">Spanning tree</span> Tree which includes all vertices of a graph

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

<span class="mw-page-title-main">Euclidean minimum spanning tree</span> Shortest network connecting points

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

<span class="mw-page-title-main">Simple polygon</span> Shape bounded by non-intersecting line segments

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

<span class="mw-page-title-main">Connectivity (graph theory)</span> Basic concept of graph theory

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

<span class="mw-page-title-main">Unit distance graph</span> Geometric graph with unit edge lengths

In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.

<span class="mw-page-title-main">Pseudotriangle</span>

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

Proximity problems is a class of problems in computational geometry which involve estimation of distances between geometric objects.

A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.

<span class="mw-page-title-main">Relative neighborhood graph</span>

In computational geometry, the relative neighborhood graph (RNG) is an undirected graph defined on a set of points in the Euclidean plane by connecting two points and by an edge whenever there does not exist a third point that is closer to both and than they are to each other. This graph was proposed by Godfried Toussaint in 1980 as a way of defining a structure from a set of points that would match human perceptions of the shape of the set.

<span class="mw-page-title-main">Pseudoforest</span> Graph with one cycle per component

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.

In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an n-vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.

<span class="mw-page-title-main">Squaregraph</span> Planar graph with quadrilateral faces

In graph theory, a branch of mathematics, a squaregraph is a type of undirected graph that can be drawn in the plane in such a way that every bounded face is a quadrilateral and every vertex with three or fewer neighbors is incident to an unbounded face.

In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.

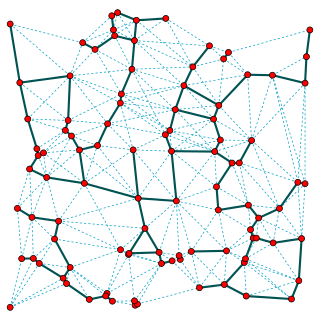
<span class="mw-page-title-main">Beta skeleton</span>

In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.

<span class="mw-page-title-main">Penny graph</span> Graph formed by touching unit circles

In geometric graph theory, a penny graph is a contact graph of unit circles. It is formed from a collection of unit circles that do not cross each other, by creating a vertex for each circle and an edge for every pair of tangent circles. The circles can be represented physically by pennies, arranged without overlapping on a flat surface, with a vertex for each penny and an edge for each two pennies that touch.

References

  1. ↑ Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. ISBN   0-387-96131-3. 1st edition; 2nd printing, corrected and expanded, 1988; Russian translation, 1989.
  2. 1 2 3 4 Eppstein, D.; Paterson, M. S.; Yao, Frances (1997). "On nearest-neighbor graphs". Discrete and Computational Geometry . 17 (3): 263–282. doi: 10.1007/PL00009293 .
  3. ↑ Miller, Gary L.; Teng, Shang-Hua; Thurston, William; Vavasis, Stephen A. (1997). "Separators for sphere-packings and nearest neighbor graphs". Journal of the Association for Computing Machinery. 44 (1): 1–29. doi: 10.1145/256292.256294 .
  4. ↑ Dong, Wei; Moses, Charikar; Li, Kai (28 March 2011). "Efficient k-nearest neighbor graph construction for generic similarity measures". Proceedings of the 20th international conference on World wide web. Association for Computing Machinery. pp. 577–586. doi:10.1145/1963405.1963487. ISBN   9781450306324. S2CID   207186093.
  5. ↑ Aggarwal, Alok; Kipnis, Shlomo (August 1988). "Lecture #10, March 10, 1988: Closest pair". In Aggarwal, Alok; Wein, Joel (eds.). Computational Geometry: Lecture Notes for 18.409, Spring 1988. Massachusetts Institute of Technology Laboratory for Computer Science. Observation 1, p. 2.
  6. ↑ Rahmati, Z.; King, V.; Whitesides, S. (2013). Kinetic data structures for all nearest neighbors and closest pair in the plane. Proceedings of the 29th ACM Symposium on Computational Geometry. pp. 137–144. doi:10.1145/2462356.2462378.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.