Negative probability

Last updated

The probability of the outcome of an experiment is never negative, although a quasiprobability distribution allows a negative probability, or quasiprobability for some events. These distributions may apply to unobservable events or conditional probabilities.

Contents

Physics and mathematics

In 1942, Paul Dirac wrote a paper "The Physical Interpretation of Quantum Mechanics" [1] where he introduced the concept of negative energies and negative probabilities:

Negative energies and probabilities should not be considered as nonsense. They are well-defined concepts mathematically, like a negative of money.

The idea of negative probabilities later received increased attention in physics and particularly in quantum mechanics. Richard Feynman argued [2] that no one objects to using negative numbers in calculations: although "minus three apples" is not a valid concept in real life, negative money is valid. Similarly he argued how negative probabilities as well as probabilities above unity possibly could be useful in probability calculations.

Negative probabilities have later been suggested to solve several problems and paradoxes. [3] Half-coins provide simple examples for negative probabilities. These strange coins were introduced in 2005 by Gábor J. Székely. [4] Half-coins have infinitely many sides numbered with 0,1,2,... and the positive even numbers are taken with negative probabilities. Two half-coins make a complete coin in the sense that if we flip two half-coins then the sum of the outcomes is 0 or 1 with probability 1/2 as if we simply flipped a fair coin.

In Convolution quotients of nonnegative definite functions [5] and Algebraic Probability Theory [6] Imre Z. Ruzsa and Gábor J. Székely proved that if a random variable X has a signed or quasi distribution where some of the probabilities are negative then one can always find two random variables, Y and Z, with ordinary (not signed / not quasi) distributions such that X, Y are independent and X + Y = Z in distribution. Thus X can always be interpreted as the "difference" of two ordinary random variables, Z and Y. If Y is interpreted as a measurement error of X and the observed value is Z then the negative regions of the distribution of X are masked / shielded by the error Y.

Another example known as the Wigner distribution in phase space, introduced by Eugene Wigner in 1932 to study quantum corrections, often leads to negative probabilities. [7] For this reason, it has later been better known as the Wigner quasiprobability distribution. In 1945, M. S. Bartlett worked out the mathematical and logical consistency of such negative valuedness. [8] The Wigner distribution function is routinely used in physics nowadays, and provides the cornerstone of phase-space quantization. Its negative features are an asset to the formalism, and often indicate quantum interference. The negative regions of the distribution are shielded from direct observation by the quantum uncertainty principle: typically, the moments of such a non-positive-semidefinite quasiprobability distribution are highly constrained, and prevent direct measurability of the negative regions of the distribution. Nevertheless, these regions contribute negatively and crucially to the expected values of observable quantities computed through such distributions.

Engineering

The concept of negative probabilities has also been proposed for reliable facility location models where facilities are subject to negatively correlated disruption risks when facility locations, customer allocation, and backup service plans are determined simultaneously. [9] [10] Li et al. [11] proposed a virtual station structure that transforms a facility network with positively correlated disruptions into an equivalent one with added virtual supporting stations, and these virtual stations were subject to independent disruptions. This approach reduces a problem from one with correlated disruptions to one without. Xie et al. [12] later showed how negatively correlated disruptions can also be addressed by the same modeling framework, except that a virtual supporting station now may be disrupted with a “failure propensity” which

... inherits all mathematical characteristics and properties of a failure probability except that we allow it to be larger than 1...

This finding paves ways for using compact mixed-integer mathematical programs to optimally design reliable location of service facilities under site-dependent and positive/negative/mixed facility disruption correlations. [13]

The proposed “propensity” concept in Xie et al. [12] turns out to be what Feynman and others referred to as “quasi-probability.” Note that when a quasi-probability is larger than 1, then 1 minus this value gives a negative probability. In the reliable facility location context, the truly physically verifiable observation is the facility disruption states (whose probabilities are ensured to be within the conventional range [0,1]), but there is no direct information on the station disruption states or their corresponding probabilities. Hence the disruption "probabilities" of the stations, interpreted as “probabilities of imagined intermediary states,” could exceed unity, and thus are referred to as quasi-probabilities.

Finance

Negative probabilities have more recently been applied to mathematical finance. In quantitative finance most probabilities are not real probabilities but pseudo probabilities, often what is known as risk neutral probabilities. [14] These are not real probabilities, but theoretical "probabilities" under a series of assumptions that help simplify calculations by allowing such pseudo probabilities to be negative in certain cases as first pointed out by Espen Gaarder Haug in 2004. [15]

A rigorous mathematical definition of negative probabilities and their properties was recently derived by Mark Burgin and Gunter Meissner (2011). The authors also show how negative probabilities can be applied to financial option pricing. [14]

Machine learning and signal processing

Some problems in machine learning use graph- or hypergraph-based formulations having edges assigned with weights, most commonly positive. A positive weight from one vertex to another can be interpreted in a random walk as a probability of getting from the former vertex to the latter. In a Markov chain that is the probability of each event depending only on the state attained in the previous event.

Some problems in machine learning, e.g., correlation clustering, naturally often deal with a signed graph where the edge weight indicates whether two nodes are similar (corelated with a positive edge weight) or dissimilar (anticorrelated with a negative edge weight). Treating a graph weight as a probability of the two vertices to be related is being replaced here with a correlation that of course can be negative or positive equally legitimately. Positive and negative graph weights are uncontroversial if interpreted as correlations rather than probabilities but raise similar issues, e.g., challenges for normalization in graph Laplacian and explainability of spectral clustering for signed graph partitioning; e.g., [16]

Similarly, in spectral graph theory, the eigenvalues of the Laplacian matrix represent frequencies and eigenvectors form what is known as a graph Fourier basis substituting the classical Fourier transform in the graph-based signal processing. In applications to imaging, the graph Laplacian is formulated analogous to the anisotropic diffusion operator where a Gaussian smoothed image is interpreted as a single time slice of the solution to the heat equation, that has the original image as its initial conditions. If the graph weight was negative, that would correspond to a negative conductivity in the heat equation, stimulating the heat concentration at the graph vertices connected by the graph edge, rather than the normal heat dissipation. While negative heat conductivity is not-physical, this effect is useful for edge-enhancing image smoothing, e.g., resulting in sharpening corners of one-dimensional signals, when used in graph-based edge-preserving smoothing. [17]

See also

Related Research Articles

<span class="mw-page-title-main">Distance</span> Separation between two points

Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria. The term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects or a degree of separation. Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.

In quantum mechanics, a density matrix is a matrix that describes an ensemble of physical systems as quantum states. It allows for the calculation of the probabilities of the outcomes of any measurements performed upon the systems of the ensemble using the Born rule. It is a generalization of the more usual state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent mixed ensembles. Mixed ensembles arise in quantum mechanics in two different situations:

  1. when the preparation of the systems lead to numerous pure states in the ensemble, and thus one must deal with the statistics of possible preparations, and
  2. when one wants to describe a physical system that is entangled with another, without describing their combined state; this case is typical for a system interacting with some environment. In this case, the density matrix of an entangled system differs from that of an ensemble of pure states that, combined, would give the same statistical results upon measurement.

In probability theory, de Finetti's theorem states that exchangeable observations are conditionally independent relative to some latent variable. An epistemic probability distribution could then be assigned to this variable. It is named in honor of Bruno de Finetti.

The Ising model, named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states. The spins are arranged in a graph, usually a lattice, allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases. The model allows the identification of phase transitions as a simplified model of reality. The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition.

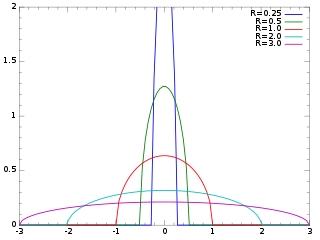
<span class="mw-page-title-main">Wigner semicircle distribution</span> Probability distribution

The Wigner semicircle distribution, named after the physicist Eugene Wigner, is the probability distribution on [−R, R] whose probability density function f is a scaled semicircle centered at :

In probability theory and mathematical physics, a random matrix is a matrix-valued random variable—that is, a matrix in which some or all of its entries are sampled randomly from a probability distribution. Random matrix theory (RMT) is the study of properties of random matrices, often as they become large. RMT provides techniques like mean-field theory, diagrammatic methods, the cavity method, or the replica method to compute quantities like traces, spectral densities, or scalar products between eigenvectors. Many physical phenomena, such as the spectrum of nuclei of heavy atoms, the thermal conductivity of a lattice, or the emergence of quantum chaos, can be modeled mathematically as problems concerning large, random matrices.

<span class="mw-page-title-main">Wigner quasiprobability distribution</span> Wigner distribution function in physics as opposed to in signal processing

The Wigner quasiprobability distribution is a quasiprobability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction that appears in Schrödinger's equation to a probability distribution in phase space.

Greek letters are used in mathematics, science, engineering, and other areas where mathematical notation is used as symbols for constants, special functions, and also conventionally for variables representing certain quantities. In these contexts, the capital letters and the small letters represent distinct and unrelated entities. Those Greek letters which have the same form as Latin letters are rarely used: capital A, B, E, Z, H, I, K, M, N, O, P, T, Y, X. Small ι, ο and υ are also rarely used, since they closely resemble the Latin letters i, o and u. Sometimes, font variants of Greek letters are used as distinct symbols in mathematics, in particular for ε/ϵ and π/ϖ. The archaic letter digamma (Ϝ/ϝ/ϛ) is sometimes used.

<span class="mw-page-title-main">Quantum tomography</span> Reconstruction of quantum states based on measurements

Quantum tomography or quantum state tomography is the process by which a quantum state is reconstructed using measurements on an ensemble of identical quantum states. The source of these states may be any device or system which prepares quantum states either consistently into quantum pure states or otherwise into general mixed states. To be able to uniquely identify the state, the measurements must be tomographically complete. That is, the measured operators must form an operator basis on the Hilbert space of the system, providing all the information about the state. Such a set of observations is sometimes called a quorum. The term tomography was first used in the quantum physics literature in a 1993 paper introducing experimental optical homodyne tomography.

In quantum mechanics, the Wigner–Weyl transform or Weyl–Wigner transform is the invertible mapping between functions in the quantum phase space formulation and Hilbert space operators in the Schrödinger picture.

A quasiprobability distribution is a mathematical object similar to a probability distribution but which relaxes some of Kolmogorov's axioms of probability theory. Quasiprobabilities share several of general features with ordinary probabilities, such as, crucially, the ability to yield expectation values with respect to the weights of the distribution. However, they can violate the σ-additivity axiom: integrating over them does not necessarily yield probabilities of mutually exclusive states. Indeed, quasiprobability distributions also have regions of negative probability density, counterintuitively, contradicting the first axiom. Quasiprobability distributions arise naturally in the study of quantum mechanics when treated in phase space formulation, commonly used in quantum optics, time-frequency analysis, and elsewhere.

<span class="mw-page-title-main">Husimi Q representation</span> Computational physics simulation tool

The Husimi Q representation, introduced by Kôdi Husimi in 1940, is a quasiprobability distribution commonly used in quantum mechanics to represent the phase space distribution of a quantum state such as light in the phase space formulation. It is used in the field of quantum optics and particularly for tomographic purposes. It is also applied in the study of quantum effects in superconductors.

In mathematics, the Fortuin–Kasteleyn–Ginibre (FKG) inequality is a correlation inequality, a fundamental tool in statistical mechanics and probabilistic combinatorics, due to Cees M. Fortuin, Pieter W. Kasteleyn, and Jean Ginibre. Informally, it says that in many random systems, increasing events are positively correlated, while an increasing and a decreasing event are negatively correlated. It was obtained by studying the random cluster model.

<span class="mw-page-title-main">Gábor J. Székely</span>

Gábor J. Székely is a Hungarian-American statistician/mathematician best known for introducing energy statistics (E-statistics). Examples include: the distance correlation, which is a bona fide dependence measure, equals zero exactly when the variables are independent; the distance skewness, which equals zero exactly when the probability distribution is diagonally symmetric; the E-statistic for normality test; and the E-statistic for clustering.

In quantum information theory, the Wehrl entropy, named after Alfred Wehrl, is a classical entropy of a quantum-mechanical density matrix. It is a type of quasi-entropy defined for the Husimi Q representation of the phase-space quasiprobability distribution. See for a comprehensive review of basic properties of classical, quantum and Wehrl entropies, and their implications in statistical mechanics.

The phase-space formulation of quantum mechanics places the position and momentum variables on equal footing in phase space. In contrast, the Schrödinger picture uses the position or momentum representations. The two key features of the phase-space formulation are that the quantum state is described by a quasiprobability distribution and operator multiplication is replaced by a star product.

<span class="mw-page-title-main">R. L. Hudson</span> British mathematician

Robin Lyth Hudson was a British mathematician notable for his contribution to quantum probability.

In mathematics, the Segal–Bargmann space, also known as the Bargmann space or Bargmann–Fock space, is the space of holomorphic functions F in n complex variables satisfying the square-integrability condition:

First passage percolation is a mathematical method used to describe the paths reachable in a random medium within a given amount of time.

References

  1. ↑ Dirac, P. A. M. (1942). "Bakerian Lecture. The Physical Interpretation of Quantum Mechanics". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 180 (980): 1–39. Bibcode:1942RSPSA.180....1D. doi: 10.1098/rspa.1942.0023 . JSTOR   97777.
  2. ↑ Feynman, Richard P. (1987). "Negative Probability" (PDF). In Peat, F. David; Hiley, Basil (eds.). Quantum Implications: Essays in Honour of David Bohm. Routledge & Kegan Paul Ltd. pp. 235–248. ISBN   978-0415069601.
  3. ↑ Khrennikov, Andrei Y. (March 7, 2013). Non-Archimedean Analysis: Quantum Paradoxes, Dynamical Systems and Biological Models. Springer Science & Business Media. ISBN   978-94-009-1483-4.
  4. ↑ Székely, G.J. (July 2005). "Half of a Coin: Negative Probabilities" (PDF). Wilmott Magazine: 66–68. Archived from the original (PDF) on 2013-11-08.
  5. ↑ Ruzsa, Imre Z.; SzéKely, Gábor J. (1983). "Convolution quotients of nonnegative functions". Monatshefte für Mathematik. 95 (3): 235–239. doi:10.1007/BF01352002. S2CID   122858460.
  6. ↑ Ruzsa, I.Z.; Székely, G.J. (1988). Algebraic Probability Theory. New York: Wiley. ISBN   0-471-91803-2.
  7. ↑ Wigner, E. (1932). "On the Quantum Correction for Thermodynamic Equilibrium". Physical Review. 40 (5): 749–759. Bibcode:1932PhRv...40..749W. doi:10.1103/PhysRev.40.749. hdl: 10338.dmlcz/141466 .
  8. ↑ Bartlett, M. S. (1945). "Negative Probability". Mathematical Proceedings of the Cambridge Philosophical Society. 41 (1): 71–73. Bibcode:1945PCPS...41...71B. doi:10.1017/S0305004100022398. S2CID   12149669.
  9. ↑ Snyder, L.V.; Daskin, M.S. (2005). "Reliability Models for Facility Location: The Expected Failure Cost Case". Transportation Science. 39 (3): 400–416. CiteSeerX   10.1.1.1.7162 . doi:10.1287/trsc.1040.0107.
  10. ↑ Cui, T.; Ouyang, Y.; Shen, Z-J. M. (2010). "Reliable Facility Location Design Under the Risk of Disruptions". Operations Research. 58 (4): 998–1011. CiteSeerX   10.1.1.367.3741 . doi:10.1287/opre.1090.0801. S2CID   6236098.
  11. ↑ Li, X.; Ouyang, Y.; Peng, F. (2013). "A supporting station model for reliable infrastructure location design under interdependent disruptions". Transportation Research Part E. 60: 80–93. doi:10.1016/j.tre.2013.06.005.
  12. 1 2 Xie, S.; Li, X.; Ouyang, Y. (2015). "Decomposition of general facility disruption correlations via augmentation of virtual supporting stations". Transportation Research Part B. 80: 64–81. doi:10.1016/j.trb.2015.06.006.
  13. ↑ Xie, Siyang; An, Kun; Ouyang, Yanfeng (2019). "Planning facility location under generally correlated facility disruptions: Use of supporting stations and quasi-probabilities". Transportation Research Part B: Methodological. 122. Elsevier BV: 115–139. doi: 10.1016/j.trb.2019.02.001 . ISSN   0191-2615.
  14. 1 2 Meissner, Gunter A.; Burgin, Dr. Mark (2011). "Negative Probabilities in Financial Modeling". SSRN Electronic Journal. Elsevier BV. doi:10.2139/ssrn.1773077. ISSN   1556-5068. S2CID   197765776.
  15. ↑ Haug, E. G. (2004). "Why so Negative to Negative Probabilities?" (PDF). Wilmott Magazine: 34–38.
  16. ↑ Knyazev, Andrew (2018). On spectral partitioning of signed graphs. Eighth SIAM Workshop on Combinatorial Scientific Computing, CSC 2018, Bergen, Norway, June 6–8. arXiv: 1701.01394 . doi: 10.1137/1.9781611975215.2 .
  17. ↑ Knyazev, A. (2015). Edge-enhancing Filters with Negative Weights. IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, 14-16 Dec.2015. pp. 260–264. arXiv: 1509.02491 . doi:10.1109/GlobalSIP.2015.7418197.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.