
The ecliptic is the plane of Earth's orbit around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the background of stars. The ecliptic is an important reference plane and is the basis of the ecliptic coordinate system.

In physics, an orbit is the gravitationally curved trajectory of an object, such as the trajectory of a planet around a star or a natural satellite around a planet. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

In the context of spaceflight, a satellite is an object that has been intentionally placed into orbit. These objects are called artificial satellites to distinguish them from natural satellites such as Earth's Moon.

Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a reference plane and the orbital plane or axis of direction of the orbiting object.
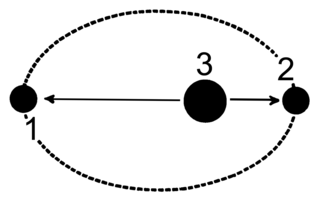
Apsis denotes either of the two extreme points in the orbit of a planetary body about its primary body. The plural term, "apsides," usually implies both apsis points ; apsides can also refer to the distance of the extreme range of an object orbiting a host body. For example, the apsides of Earth's orbit of the Sun are two: the apsis for Earth's farthest point from the Sun, dubbed the aphelion; and the apsis for Earth's nearest point, the perihelion. .
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes, each consisting of a set of six parameters, are commonly used in astronomy and orbital mechanics.

Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics to astronomical objects, such as stars and planets, to produce ephemeris data.

The orbital period is the time a given astronomical object takes to complete one orbit around another object, and applies in astronomy usually to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars.
A geocentric orbit or Earth orbit involves any object orbiting the Earth, such as the Moon or artificial satellites. In 1997 NASA estimated there were approximately 2,465 artificial satellite payloads orbiting the Earth and 6,216 pieces of space debris as tracked by the Goddard Space Flight Center. Over 16,291 previously launched objects have decayed into the Earth's atmosphere.

In geodesy, a reference ellipsoid is a mathematically defined surface that approximates the geoid, which is the truer, imperfect figure of the Earth, or other planetary body, as opposed to a perfect, smooth, and unaltered sphere, which factors in the undulations of the bodies' gravity due to variations in the composition and density of the interior, as well as the subsequent flattening caused by the centrifugal force from the rotation of these massive objects . Because of their relative simplicity, reference ellipsoids are used as a preferred surface on which geodetic network computations are performed and point coordinates such as latitude, longitude, and elevation are defined.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
Cassini's laws provide a compact description of the motion of the Moon. They were established in 1693 by Giovanni Domenico Cassini, a prominent scientist of his time.

An orbital pole is either point at the ends of an imaginary line segment that runs through the center of an orbit and is perpendicular to the orbital plane. Projected onto the celestial sphere, orbital poles are similar in concept to celestial poles, but are based on the body's orbit instead of its equator.

A ground track or ground trace is the path on the surface of a planet directly below an aircraft's or satellite's trajectory. In the case of satellites, it is also known as a suborbital track, and is the vertical projection of the satellite's orbit onto the surface of the Earth.
The poles of astronomical bodies are determined based on their axis of rotation in relation to the celestial poles of the celestial sphere. Astronomical bodies include stars, planets, dwarf planets and small Solar System bodies such as comets and minor planets, as well as natural satellites and minor-planet moons.

Earth-centered inertial (ECI) coordinate frames have their origins at the center of mass of Earth and are fixed with respect to the stars. "I" in "ECI" stands for inertial, in contrast to the "Earth-centered - Earth-fixed" (ECEF) frames, which rotate with respect to stars.

The beta angle is a measurement that is used most notably in orbital spaceflight. The beta angle determines the percentage of time that a satellite in low Earth orbit (LEO) spends in direct sunlight, absorbing solar energy. The term is defined as the angle between the orbital plane of the satellite and the vector to the Sun. The beta angle is the smaller of the two angles between the Sun vector and the plane of the object's orbit. The beta angle does not define a unique orbital plane; all satellites in orbit with a given beta angle at a given altitude have the same exposure to the Sun, even though they may be orbiting in completely different planes around Earth.

Retrograde motion in astronomy is, in general, orbital or rotational motion of an object in the direction opposite the rotation of its primary, that is, the central object. It may also describe other motions such as precession or nutation of an object's rotational axis. Prograde or direct motion is more normal motion in the same direction as the primary rotates. However, "retrograde" and "prograde" can also refer to an object other than the primary if so described. The direction of rotation is determined by an inertial frame of reference, such as distant fixed stars.
This glossary of astronomy is a list of definitions of terms and concepts relevant to astronomy and cosmology, their sub-disciplines, and related fields. Astronomy is concerned with the study of celestial objects and phenomena that originate outside the atmosphere of Earth. The field of astronomy features an extensive vocabulary and a significant amount of jargon.














