Pitch circularity is a fixed series of tones that are perceived to ascend or descend endlessly in pitch. It's an example of an auditory illusion.

Pitch circularity is a fixed series of tones that are perceived to ascend or descend endlessly in pitch. It's an example of an auditory illusion.
Pitch is often defined as extending along a one-dimensional continuum from high to low, as can be experienced by sweeping one’s hand up or down a piano keyboard. This continuum is known as pitch height. However pitch also varies in a circular fashion, known as pitch class: as one plays up a keyboard in semitone steps, C, C♯, D, D♯, E, F, F♯, G, G♯, A, A♯ and B sound in succession, followed by C again, but one octave higher. Because the octave is the most consonant interval after the unison, tones that stand in octave relation, and are so of the same pitch class, have a certain perceptual equivalence—all Cs sound more alike to other Cs than to any other pitch class, as do all D♯s, and so on; this creates the auditory equivalent of a Barber's pole, where all tones of the same pitch class are located on the same side of the pole, but at different heights.
Researchers have demonstrated that by creating banks of tones whose note names are clearly defined perceptually but whose perceived heights are ambiguous, one can create scales that appear to ascend or descend endlessly in pitch. Roger Shepard achieved this ambiguity of height by creating banks of complex tones, with each tone composed only of components that stood in octave relationship. In other words, the components of the complex tone C consisted only of Cs, but in different octaves, and the components of the complex tone F♯ consisted only of F♯s, but in different octaves. [2] When such complex tones are played in semitone steps the listener perceives a scale that appears to ascend endlessly in pitch. Jean-Claude Risset achieved the same effect using gliding tones instead, so that a single tone appeared to glide up or down endlessly in pitch. [3] Circularity effects based on this principle have been produced in orchestral music and electronic music, by having multiple instruments playing simultaneously in different octaves.
Normann et al. [4] showed that pitch circularity can be created using a bank of single tones; here the relative amplitudes of the odd and even harmonics of each tone are manipulated so as to create ambiguities of height. A different algorithm that creates ambiguities of pitch height by manipulating the relative amplitudes of the odd and even harmonics, was developed by Diana Deutsch and colleagues. [5] Using this algorithm, gliding tones that appear to ascend or descend endlessly are also produced. This development has led to the intriguing possibility that, using this new algorithm, one might transform banks of natural instrument samples so as to produce tones that sound like those of natural instruments but still have the property of circularity. This development opens up new avenues for music composition and performance. [6]
In music, an octave or perfect octave is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". The interval between the first and second harmonics of the harmonic series is an octave.
In music theory, a scale is any set of musical notes ordered by fundamental frequency or pitch. A scale ordered by increasing pitch is an ascending scale, and a scale ordered by decreasing pitch is a descending scale.
A strange loop is a cyclic structure that goes through several levels in a hierarchical system. It arises when, by moving only upwards or downwards through the system, one finds oneself back where one started. Strange loops may involve self-reference and paradox. The concept of a strange loop was proposed and extensively discussed by Douglas Hofstadter in Gödel, Escher, Bach, and is further elaborated in Hofstadter's book I Am a Strange Loop, published in 2007.

A Shepard tone, named after Roger Shepard, is a sound consisting of a superposition of sine waves separated by octaves. When played with the bass pitch of the tone moving upward or downward, it is referred to as the Shepard scale. This creates the auditory illusion of a tone that seems to continually ascend or descend in pitch, yet which ultimately gets no higher or lower.
In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones. For instance, the interval from F up to the B above it is a tritone as it can be decomposed into the three adjacent whole tones F–G, G–A, and A–B.

Pitch is a perceptual property of sounds that allows their ordering on a frequency-related scale, or more commonly, pitch is the quality that makes it possible to judge sounds as "higher" and "lower" in the sense associated with musical melodies. Pitch is a major auditory attribute of musical tones, along with duration, loudness, and timbre.
Auditory illusions are false perceptions of a real sound or outside stimulus. These false perceptions are the equivalent of an optical illusion: the listener hears either sounds which are not present in the stimulus, or sounds that should not be possible given the circumstance on how they were created.

In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths.. If C is chosen as a starting point, the sequence is: C, G, D, A, E, B, F♯, C♯, A♭, E♭, B♭, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle.
The octave illusion is an auditory illusion discovered by Diana Deutsch in 1973. It is produced when two tones that are an octave apart are repeatedly played in alternation ("high-low-high-low") through stereo headphones. The same sequence is played to both ears simultaneously; however when the right ear receives the high tone, the left ear receives the low tone, and conversely. Instead of hearing two alternating pitches, most subjects instead hear a single tone that alternates between ears while at the same time its pitch alternates between high and low.
The glissando illusion is an auditory illusion, created when a sound with a fixed pitch, such as a synthesized oboe tone, is played together with a sine wave gliding up and down in pitch, and they are both switched back and forth between stereo loudspeakers. The effect is that the oboe is heard as switching between loudspeakers while the sine wave is heard as joined together seamlessly, and as moving around in space in accordance with its pitch motion. Right-handers often hear the glissando as traveling from left to right as its pitch glides from low to high, and then back from right to left as its pitch glides from high to low.

The tritone paradox is an auditory illusion in which a sequentially played pair of Shepard tones separated by an interval of a tritone, or half octave, is heard as ascending by some people and as descending by others. Different populations tend to favor one of a limited set of different spots around the chromatic circle as central to the set of "higher" tones. Roger Shepard in 1963 had argued that such tone pairs would be heard ambiguously as either ascending or descending. However, psychology of music researcher Diana Deutsch in 1986 discovered that when the judgments of individual listeners were considered separately, their judgments depended on the positions of the tones along the chromatic circle. For example, one listener would hear the tone pair C–F♯ as ascending and the tone pair G–C♯ as descending. Yet another listener would hear the tone pair C–F♯ as descending and the tone pair G–C♯ as ascending. Furthermore, the way these tone pairs were perceived varied depending on the listener's language or dialect.
Piano acoustics is the set of physical properties of the piano that affect its sound. It is an area of study within musical acoustics.
Deutsch's scale illusion is an auditory illusion in which two series of unconnected notes appear to combine into a single recognisable melody, when played simultaneously into the left and right ears of a listener.
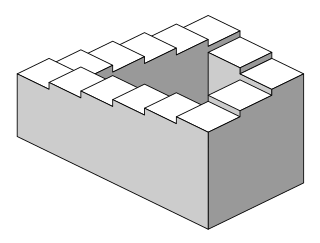
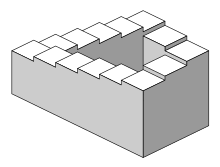
The Penrose stairs or Penrose steps, also dubbed the impossible staircase, is an impossible object created by Oscar Reutersvärd in 1937 and later independently discovered and made popular by Lionel Penrose and his son Roger Penrose. A variation on the Penrose triangle, it is a two-dimensional depiction of a staircase in which the stairs make four 90-degree turns as they ascend or descend yet form a continuous loop, so that a person could climb them forever and never get any higher. This is clearly impossible in three-dimensional Euclidean geometry but possible in some non-Euclidean geometry like in nil geometry.

Jean-Claude Raoul Olivier Risset was a French composer, best known for his pioneering contributions to computer music. He was a former student of André Jolivet and former co-worker of Max Mathews at Bell Labs.

Scientific pitch notation (SPN), also known as American standard pitch notation (ASPN) and international pitch notation (IPN), is a method of specifying musical pitch by combining a musical note name and a number identifying the pitch's octave.

A heptatonic scale is a musical scale that has seven pitches, or tones, per octave. Examples include the major scale or minor scale; e.g., in C major: C D E F G A B C—and in the relative minor, A minor, natural minor: A B C D E F G A; the melodic minor scale, A B C D E F♯G♯A ascending, A G F E D C B A descending; the harmonic minor scale, A B C D E F G♯A; and a scale variously known as the Byzantine, and Hungarian, scale, C D E♭ F♯ G A♭ B C. Indian classical theory postulates seventy-two seven-tone scale types, collectively called thaat, whereas others postulate twelve or ten seven-tone scale types.
Diana Deutsch is a British-American psychologist from London, England. She's a Professor of Psychology at the University of California, San Diego, and is a prominent researcher on the psychology of music. Deutsch is primarily known for her discoveries in music and speech illusions. She also studies the cognitive foundation of musical grammars, which consists of the way people hold musical pitches in memory, and how people relate the sounds of music and speech to each other. In addition, she is known for her work on absolute pitch, which she has shown is far more prevalent among speakers of tonal languages. Deutsch is the author of Musical Illusions and Phantom Words: How Music and Speech Unlock Mysteries of the Brain (2019), the Psychology of Music, and also the compact discs Musical Illusions and Paradoxes (1995) and Phantom Words and Other Curiosities (2003).

Diatonic and chromatic are terms in music theory that are most often used to characterize scales, and are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900.

Illusory conjunctions are psychological effects in which participants combine features of two objects into one object. There are visual illusory conjunctions, auditory illusory conjunctions, and illusory conjunctions produced by combinations of visual and tactile stimuli. Visual illusory conjunctions are thought to occur due to a lack of visual spatial attention, which depends on fixation and the amount of time allotted to focus on an object. With a short span of time to interpret an object, blending of different aspects within a region of the visual field – like shapes and colors – can occasionally be skewed, which results in visual illusory conjunctions. For example, in a study designed by Anne Treisman and Schmidt, participants were required to view a visual presentation of numbers and shapes in different colors. Some shapes were larger than others but all shapes and numbers were evenly spaced and shown for just 200 ms. When the participants were asked to recall the shapes they reported answers such as a small green triangle instead of a small green circle. If the space between the objects is smaller, illusory conjunctions occur more often.
{{cite journal}}: CS1 maint: multiple names: authors list (link) PDF Document {{cite journal}}: CS1 maint: multiple names: authors list (link) Weblink PDF Document