
In optics, the refractive index of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation. An elliptically polarized wave may be resolved into two linearly polarized waves in phase quadrature, with their polarization planes at right angles to each other. Since the electric field can rotate clockwise or counterclockwise as it propagates, elliptically polarized waves exhibit chirality.
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source. Even when there is a propagating electromagnetic wave produced, one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths.

An optical prism is a transparent optical element with flat, polished surfaces that are designed to refract light. At least one surface must be angled — elements with two parallel surfaces are not prisms. The most familiar type of optical prism is the triangular prism, which has a triangular base and rectangular sides. Not all optical prisms are geometric prisms, and not all geometric prisms would count as an optical prism. Prisms can be made from any material that is transparent to the wavelengths for which they are designed. Typical materials include glass, acrylic and fluorite.
A transverse mode of electromagnetic radiation is a particular electromagnetic field pattern of the radiation in the plane perpendicular to the radiation's propagation direction. Transverse modes occur in radio waves and microwaves confined to a waveguide, and also in light waves in an optical fiber and in a laser's optical resonator.
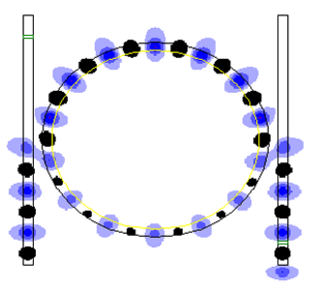
An optical ring resonator is a set of waveguides in which at least one is a closed loop coupled to some sort of light input and output. The concepts behind optical ring resonators are the same as those behind whispering galleries except that they use light and obey the properties behind constructive interference and total internal reflection. When light of the resonant wavelength is passed through the loop from the input waveguide, the light builds up in intensity over multiple round-trips owing to constructive interference and is output to the output bus waveguide which serves as a detector waveguide. Because only a select few wavelengths will be at resonance within the loop, the optical ring resonator functions as a filter. Additionally, as implied earlier, two or more ring waveguides can be coupled to each other to form an add/drop optical filter.
An optical waveguide is a physical structure that guides electromagnetic waves in the optical spectrum. Common types of optical waveguides include optical fiber waveguides, transparent dielectric waveguides made of plastic and glass, liquid light guides, and liquid waveguides.

Double-clad fiber (DCF) is a class of optical fiber with a structure consisting of three layers of optical material instead of the usual two. The inner-most layer is called the core. It is surrounded by the inner cladding, which is surrounded by the outer cladding. The three layers are made of materials with different refractive indices.

In optics, a dispersive prism is an optical prism that is used to disperse light, that is, to separate light into its spectral components. Different wavelengths (colors) of light will be deflected by the prism at different angles. This is a result of the prism material's index of refraction varying with wavelength (dispersion). Generally, longer wavelengths (red) undergo a smaller deviation than shorter wavelengths (blue). The dispersion of white light into colors by a prism led Sir Isaac Newton to conclude that white light consisted of a mixture of different colors.

Acousto-optics is a branch of physics that studies the interactions between sound waves and light waves, especially the diffraction of laser light by ultrasound through an ultrasonic grating.
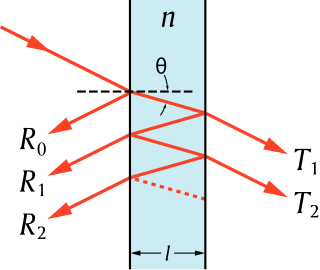
The transfer-matrix method is a method used in optics and acoustics to analyze the propagation of electromagnetic or acoustic waves through a stratified medium; a stack of thin films. This is, for example, relevant for the design of anti-reflective coatings and dielectric mirrors.
Eigenmode expansion (EME) is a computational electrodynamics modelling technique. It is also referred to as the mode matching technique or the bidirectional eigenmode propagation method. Eigenmode expansion is a linear frequency-domain method.

Thin-film interference is a natural phenomenon in which light waves reflected by the upper and lower boundaries of a thin film interfere with one another, increasing reflection at some wavelengths and decreasing it at others. When white light is incident on a thin film, this effect produces colorful reflections.
Leaky-wave antenna (LWA) belong to the more general class of traveling wave antenna, that use a traveling wave on a guiding structure as the main radiating mechanism. Traveling-wave antenna fall into two general categories, slow-wave antennas and fast-wave antennas, which are usually referred to as leaky-wave antennas.
Holographic optical element (HOE) is an optical component (mirror, lens, directional diffuser, etc.) that produces holographic images using principles of diffraction. HOE is most commonly used in transparent displays, 3D imaging, and certain scanning technologies. The shape and structure of the HOE is dependent on the piece of hardware it is needed for, and the coupled wave theory is a common tool used to calculate the diffraction efficiency or grating volume that helps with the design of an HOE. Early concepts of the holographic optical element can be traced back to the mid-1900s, coinciding closely with the start of holography coined by Dennis Gabor. The application of 3D visualization and displays is ultimately the end goal of the HOE; however, the cost and complexity of the device has hindered the rapid development toward full 3D visualization. The HOE is also used in the development of augmented reality(AR) by companies such as Google with Google Glass or in research universities that look to utilize HOEs to create 3D imaging without the use of eye-wear or head-wear. Furthermore, the ability of the HOE to allow for transparent displays have caught the attention of the US military in its development of better head-up displays (HUD) which is used to display crucial information for aircraft pilots.
Marcatili’s method is an approximate analytical method that describes how light propagates through rectangular dielectric optical waveguides. It was published by Enrique Marcatili in 1969.
Surface plasmon resonance microscopy (SPRM), also called surface plasmon resonance imaging (SPRI), is a label free analytical tool that combines the surface plasmon resonance of metallic surfaces with imaging of the metallic surface. The heterogeneity of the refractive index of the metallic surface imparts high contrast images, caused by the shift in the resonance angle. SPRM can achieve a sub-nanometer thickness sensitivity and lateral resolution achieves values of micrometer scale. SPRM is used to characterize surfaces such as self-assembled monolayers, multilayer films, metal nanoparticles, oligonucleotide arrays, and binding and reduction reactions. Surface plasmon polaritons are surface electromagnetic waves coupled to oscillating free electrons of a metallic surface that propagate along a metal/dielectric interface. Since polaritons are highly sensitive to small changes in the refractive index of the metallic material, it can be used as a biosensing tool that does not require labeling. SPRM measurements can be made in real-time, such as measuring binding kinetics of membrane proteins in single cells, or DNA hybridization.
An Edge Emitting LED (ELED) fulfills the requirement of high brightness LED, which provides high-efficiency coupling to optical fibers.
The operation of a photon scanning tunneling microscope (PSTM) is analogous to the operation of an electron scanning tunneling microscope, with the primary distinction being that PSTM involves tunneling of photons instead of electrons from the sample surface to the probe tip. A beam of light is focused on a prism at an angle greater than the critical angle of the refractive medium in order to induce total internal reflection within the prism. Although the beam of light is not propagated through the surface of the refractive prism under total internal reflection, an evanescent field of light is still present at the surface.
Optical holography is a technique which enables an optical wavefront to be recorded and later re-constructed. Holography is best known as a method of generating three-dimensional images but it also has a wide range of other applications.























