The Euler product formula
The Euler product formula for the Riemann zeta function reads
where the left hand side equals the Riemann zeta function:
and the product on the right hand side extends over all prime numbers p:
Leonhard Euler proved the Euler product formula for the Riemann zeta function in his thesis Variae observationes circa series infinitas (Various Observations about Infinite Series), published by St Petersburg Academy in 1737. [1] [2]
The Euler product formula for the Riemann zeta function reads
where the left hand side equals the Riemann zeta function:
and the product on the right hand side extends over all prime numbers p:

This sketch of a proof makes use of simple algebra only. This was the method by which Euler originally discovered the formula. There is a certain sieving property that we can use to our advantage:
Subtracting the second equation from the first we remove all elements that have a factor of 2:
Repeating for the next term:
Subtracting again we get:
where all elements having a factor of 3 or 2 (or both) are removed.
It can be seen that the right side is being sieved. Repeating infinitely for where is prime, we get:
Dividing both sides by everything but the ζ(s) we obtain:
This can be written more concisely as an infinite product over all primes p:
To make this proof rigorous, we need only to observe that when , the sieved right-hand side approaches 1, which follows immediately from the convergence of the Dirichlet series for .
An interesting result can be found for ζ(1), the harmonic series:
which can also be written as,
which is,
as,
thus,
While the series ratio test is inconclusive for the left-hand side it may be shown divergent by bounding logarithms. Similarly for the right-hand side the infinite coproduct of reals greater than one does not guarantee divergence, e.g.,
Instead, the denominator may be written in terms of the primorial numerator so that divergence is clear
given the trivial composed logarithmic divergence of an inverse prime series.
Each factor (for a given prime p) in the product above can be expanded to a geometric series consisting of the reciprocal of p raised to multiples of s, as follows
When , this series converges absolutely. Hence we may take a finite number of factors, multiply them together, and rearrange terms. Taking all the primes p up to some prime number limit q, we have
where σ is the real part of s. By the fundamental theorem of arithmetic, the partial product when expanded out gives a sum consisting of those terms n−s where n is a product of primes less than or equal to q. The inequality results from the fact that therefore only integers larger than q can fail to appear in this expanded out partial product. Since the difference between the partial product and ζ(s) goes to zero when σ > 1, we have convergence in this region.

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 32. The smallest positive square-free numbers are

In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as or , and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.
The Liouville Lambda function, denoted by λ(n) and named after Joseph Liouville, is an important arithmetic function. Its value is +1 if n is the product of an even number of prime numbers, and −1 if it is the product of an odd number of primes.

Euler's constant is a mathematical constant, usually denoted by the lowercase Greek letter gamma, defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by log:

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:

The sum of the reciprocals of all prime numbers diverges; that is:
In mathematics, a Dirichlet series is any series of the form
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The original such product was given for the sum of all positive integers raised to a certain power as proven by Leonhard Euler. This series and its continuation to the entire complex plane would later become known as the Riemann zeta function.

In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0, −1, −2, … by

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.
The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up years later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
In mathematics, Apéry's theorem is a result in number theory that states the Apéry's constant ζ(3) is irrational. That is, the number
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.
In mathematics, the Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted ζ(s) and is named after the mathematician Bernhard Riemann. When the argument s is a real number greater than one, the zeta function satisfies the equation
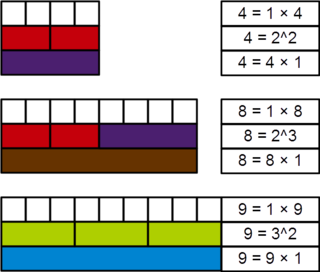
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, n is a perfect power if there exist natural numbers m > 1, and k > 1 such that mk = n. In this case, n may be called a perfect kth power. If k = 2 or k = 3, then n is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers.
In number theory, Ramanujan's sum, usually denoted cq(n), is a function of two positive integer variables q and n defined by the formula
In mathematics, the prime zeta function is an analogue of the Riemann zeta function, studied by Glaisher (1891). It is defined as the following infinite series, which converges for :
In mathematics, the multiple zeta functions are generalizations of the Riemann zeta function, defined by
In number theory, the totient summatory function is a summatory function of Euler's totient function defined by: