Proximity analysis

Last updated December 20, 2023

Proximity analysis is a class of spatial analysis tools and algorithms that employ geographic distance as a central principle.^[1] Distance is fundamental to geographic inquiry and spatial analysis, due to principles such as the friction of distance, Tobler's first law of geography, and Spatial autocorrelation, which are incorporated into analytical tools.^[2] Proximity methods are thus used in a variety of applications, especially those that involve movement and interaction.

Distance measures

All proximity analysis tools are based on a measure of distance between two locations. This may seen as a simplistic geometric measurement, but the nature of geographic phenomena and geographic activity requires several candidate methods to measure and express distance and distance-related measures.^[2]

Euclidean distance, the straight-line geometric distance measured on a planar surface. In geographic information systems, this can be easily calculated from locations in a cartesian Projected coordinate system using the Pythagorean theorem. While it is the simplest method to measure distance, it rarely reflects actual geographic movement.
Manhattan distance, the distance between two locations in a cartesian (planar) coordinate system along a path that only follows the x and y axes (thus appearing similar to a path through a grid street network such as that of Manhattan).
Geodesic distance, the shortest distance between two locations that stays on the surface of the Earth, following a great circle. On a sphere, the formula uses the spherical law of cosines, but the method is significantly more difficult on an ellipsoid.
Network distance, a measurement between two locations along a route within a constrained linear space, such as a road or utility network.
Abstract distance, a measurement of distance in a space that is only indirectly related to geographic space, or only metaphorically spatial. Examples include social networks of interpersonal connections, information spaces of related concepts, and the hypertext network of the World Wide Web. Although these are not inherently geographic, projecting them into an abstract space allows geographic tools such as proximity analysis to be used to study them.^[3]
Cost distance, a measurement along a route (in any of the above spaces) in which geometric distance is replaced by some other quantity that accumulates along the route (and is thus proportional to distance), called a cost because it generally serves as an undesirable quantity to be minimized.^[4] Travel time is the most common cost measurement, but other costs include carbon emissions, fuel consumption, environmental impacts, and construction costs.

Techniques

There are a variety of tools, models, and algorithms that incorporate geographic distance, due to the variety of relevant problems and tasks.^[5]

Buffers, a tool for determining the region that is within a specified distance of a set of geographic features.
Cost distance analysis, algorithms for finding optimal routes through continuous space that minimize distance and/or other location dependent costs.^[4]
Voronoi diagram, also known as Thiessen polygons, an algorithm for partitioning continuous space into a set of regions based on a set of point locations, such that each region consists of locations that are closer to one of the points than any others.^[6]
Distance decay, based on the Inverse square law, a mathematical model of how the influence of a phenomenon tends to be inversely proportional to the distance from it. A Gravity model is a similar model.
Location analysis, a set of (usually heuristic) algorithms for finding the optimal locations of a limited set of points (e.g., store locations) that minimize the aggregate distance to another set of points (e.g., customer locations). A commonly used example is Lloyd's algorithm.
Distance matrix, an array containing the distances (Euclidean or otherwise) between any two points in a set. This is frequently used as the independent variable in statistical tests of whether the strength of a relationship is correlated with distance, such as the volume of trade between cities.

Transport network analysis, a set of algorithms and tools for solving a number of distance routing problems when travel is constrained to a network of one-dimensional lines, such as roads and utility networks.^[7] For example, the common task of finding the shortest route from point A to point B, which is typically solved using Dijkstra's algorithm

Related Research Articles

A geographic information system (GIS) consists of integrated computer hardware and software that store, manage, analyze, edit, output, and visualize geographic data. Much of this often happens within a spatial database, however, this is not essential to meet the definition of a GIS. In a broader sense, one may consider such a system also to include human users and support staff, procedures and workflows, the body of knowledge of relevant concepts and methods, and institutional organizations.

A GIS file format is a standard for encoding geographical information into a computer file, as a specialized type of file format for use in geographic information systems (GIS) and other geospatial applications. Since the 1970s, dozens of formats have been created based on various data models for various purposes. They have been created by government mapping agencies, GIS software vendors, standards bodies such as the Open Geospatial Consortium, informal user communities, and even individual developers.

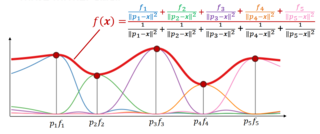
Inverse distance weighting (IDW) is a type of deterministic method for multivariate interpolation with a known scattered set of points. The assigned values to unknown points are calculated with a weighted average of the values available at the known points. This method can also be used to create spatial weights matrices in spatial autocorrelation analyses.

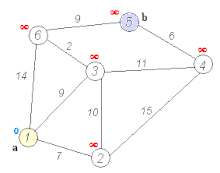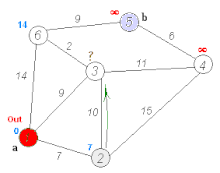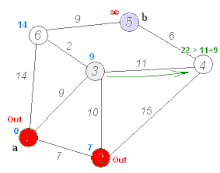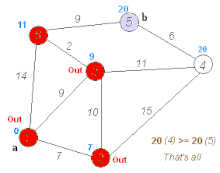
A transport network, or transportation network, is a network or graph in geographic space, describing an infrastructure that permits and constrains movement or flow. Examples include but are not limited to road networks, railways, air routes, pipelines, aqueducts, and power lines. The digital representation of these networks, and the methods for their analysis, is a core part of spatial analysis, geographic information systems, public utilities, and transport engineering. Network analysis is an application of the theories and algorithms of graph theory and is a form of proximity analysis.

Linear referencing, also called linear reference system or linear referencing system (LRS), is a method of spatial referencing in engineering and construction, in which the locations of physical features along a linear element are described in terms of measurements from a fixed point, such as a milestone along a road. Each feature is located by either a point or a line. If a segment of the linear element or route is changed, only those locations on the changed segment need to be updated. Linear referencing is suitable for management of data related to linear features like roads, railways, oil and gas transmission pipelines, power and data transmission lines, and rivers.

A spatial network is a graph in which the vertices or edges are spatial elements associated with geometric objects, i.e., the nodes are located in a space equipped with a certain metric. The simplest mathematical realization of spatial network is a lattice or a random geometric graph, where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transportation and mobility networks, Internet, mobile phone networks, power grids, social and contact networks and biological neural networks are all examples where the underlying space is relevant and where the graph's topology alone does not contain all the information. Characterizing and understanding the structure, resilience and the evolution of spatial networks is crucial for many different fields ranging from urbanism to epidemiology.

Spatial network analysis software packages are analytic software used to prepare graph-based analysis of spatial networks. They stem from research fields in transportation, architecture, and urban planning. The earliest examples of such software include the work of Garrison (1962), Kansky (1963), Levin (1964), Harary (1969), Rittel (1967), Tabor (1970) and others in the 1960s and 70s. Specific packages address their domain-specific needs, including TransCAD for transportation, GIS for planning and geography, and Axman for Space syntax researchers.

ArcGIS is a family of client, server and online geographic information system (GIS) software developed and maintained by Esri.

<span class="mw-page-title-main">Spatial analysis</span> Formal techniques which study entities using their topological, geometric, or geographic properties

Spatial analysis is any of the formal techniques which studies entities using their topological, geometric, or geographic properties. Spatial analysis includes a variety of techniques using different analytic approaches, especially spatial statistics. It may be applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, or to chip fabrication engineering, with its use of "place and route" algorithms to build complex wiring structures. In a more restricted sense, spatial analysis is geospatial analysis, the technique applied to structures at the human scale, most notably in the analysis of geographic data. It may also be applied to genomics, as in transcriptomics data.

A spatial database is a general-purpose database that has been enhanced to include spatial data that represents objects defined in a geometric space, along with tools for querying and analyzing such data.

Geomorphometry, or geomorphometrics, is the science and practice of measuring the characteristics of terrain, the shape of the surface of the Earth, and the effects of this surface form on human and natural geography. It gathers various mathematical, statistical and image processing techniques that can be used to quantify morphological, hydrological, ecological and other aspects of a land surface. Common synonyms for geomorphometry are geomorphological analysis, terrain morphometry, terrain analysis, and land surface analysis. Geomorphometrics is the discipline based on the computational measures of the geometry, topography and shape of the Earth's horizons, and their temporal change. This is a major component of geographic information systems (GIS) and other software tools for spatial analysis.

Friction of distance is a core principle of geography that states that movement incurs some form of cost, in the form of physical effort, energy, time, and/or the expenditure of other resources, and that these costs are proportional to the distance traveled. This cost is thus a resistance against movement, analogous to the effect of friction against movement in classical mechanics. The subsequent preference for minimizing distance and its cost underlies a vast array of geographic patterns from economic agglomeration to wildlife migration, as well as many of the theories and techniques of spatial analysis, such as Tobler's first law of geography, network routing, and cost distance analysis. To a large degree, friction of distance is the primary reason why geography is relevant to many aspects of the world, although its importance has been decreasing with the development of transportation and communication technologies.

Map algebra is an algebra for manipulating geographic data, primarily fields. Developed by Dr. Dana Tomlin and others in the late 1970s, it is a set of primitive operations in a geographic information system (GIS) which allows one or more raster layers ("maps") of similar dimensions to produce a new raster layer (map) using mathematical or other operations such as addition, subtraction etc.

In geographic information systems (GIS) and spatial analysis, buffer analysis is the determination of a zone around a geographic feature containing locations that are within a specified distance of that feature, the buffer zone. A buffer is likely the most commonly used tool within the proximity analysis methods.

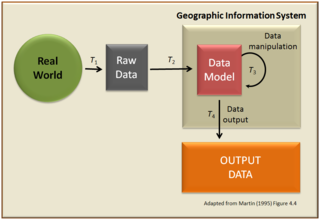
A geographic data model, geospatial data model, or simply data model in the context of geographic information systems, is a mathematical and digital structure for representing phenomena over the Earth. Generally, such data models represent various aspects of these phenomena by means of geographic data, including spatial locations, attributes, change over time, and identity. For example, the vector data model represents geography as collections of points, lines, and polygons, and the raster data model represent geography as cell matrices that store numeric values. Data models are implemented throughout the GIS ecosystem, including the software tools for data management and spatial analysis, data stored in a variety of GIS file formats, specifications and standards, and specific designs for GIS installations.

A geometric network is an object commonly used in geographic information systems to model a series of interconnected features. A geometric network is similar to a graph in mathematics and computer science, and can be described and analyzed using theories and concepts similar to graph theory. Geometric networks are often used to model road networks and public utility networks. Geometric networks are called in recent years very often spatial networks.

<span class="mw-page-title-main">Geospatial topology</span> Type of spatial relationship

Geospatial topology is the study and application of qualitative spatial relationships between geographic features, or between representations of such features in geographic information, such as in geographic information systems (GIS). For example, the fact that two regions overlap or that one contains the other are examples of topological relationships. It is thus the application of the mathematics of topology to GIS, and is distinct from, but complementary to the many aspects of geographic information that are based on quantitative spatial measurements through coordinate geometry. Topology appears in many aspects of geographic information science and GIS practice, including the discovery of inherent relationships through spatial query, vector overlay and map algebra; the enforcement of expected relationships as validation rules stored in geospatial data; and the use of stored topological relationships in applications such as network analysis. Spatial topology is the generalization of geospatial topology for non-geographic domains, e.g., CAD software.

In spatial analysis and geographic information systems, cost distance analysis or cost path analysis is a method for determining one or more optimal routes of travel through unconstrained (two-dimensional) space. The optimal solution is that which minimizes the total cost of the route, based on a field of cost density that varies over space due to local factors. It is thus based on the fundamental geographic principle of Friction of distance. It is an optimization problem with multiple deterministic algorithm solutions, implemented in most GIS software.

Vector overlay is an operation in a geographic information system (GIS) for integrating two or more vector spatial data sets. Terms such as polygon overlay, map overlay, and topological overlay are often used synonymously, although they are not identical in the range of operations they include. Overlay has been one of the core elements of spatial analysis in GIS since its early development. Some overlay operations, especially Intersect and Union, are implemented in all GIS software and are used in a wide variety of analytical applications, while others are less common.

A spatial join is an operation in a geographic information system (GIS) or spatial database that combines the attribute tables of two spatial layers based on a desired spatial relation between their geometries. It is similar to the table join operation in relational databases in merging two tables, but each pair of rows is correlated based on some form of matching location rather than a common key value. It is also similar to vector overlay operations common in GIS software such as Intersect and Union in merging two spatial datasets, but the output does not contain a composite geometry, only merged attributes.

References

↑ Blinn, Charles R., Lloyd P. Queen, and Les W. Maki, "Geographic Information Systems: A Glossary." Archived 2010-03-22 at the Wayback Machine
1 2 Sarkar, D. "FC-42 - Distance Operations". GIS&T Body of Knowledge. UCGIS. Retrieved 5 January 2023.
↑ Agarwal, Pragya; Skupin, André (2008). Self-organizing maps: Applications in geographic information science. Wiley. ISBN 9780470021675.
1 2 "How cost distance tools work". ArcGIS Pro Documentation. Esri. Retrieved 5 January 2023.
↑ de Smith, Michael J.; Goodchild, Michael F.; Longley, Paul A. (2018). "4.4 Distance Operations". Geospatial Analysis: A Comprehensive Guide to Principles, Techniques, and Software Tools (6th ed.).
↑ "25.1.18.81 Voronoi polygons". QGIS 3.22 Documentation. OSGEO. Retrieved 5 January 2023.
↑ "Network Analyst solvers". ArcGIS Pro Documentation. Esri. Retrieved 5 January 2023.

External links

Proximity tools in Esri ArcGIS
OGC ST_DWithin function (PostGIS implementation)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Blinn, Charles R., Lloyd P. Queen, and Les W. Maki, "Geographic Information Systems: A Glossary." Archived 2010-03-22 at the Wayback Machine

[sarkar-2] 1 2 Sarkar, D. "FC-42 - Distance Operations". GIS&T Body of Knowledge. UCGIS. Retrieved 5 January 2023.

[3] Agarwal, Pragya; Skupin, André (2008). Self-organizing maps: Applications in geographic information science. Wiley. ISBN 9780470021675.

[arcgis_cost-4] 1 2 "How cost distance tools work". ArcGIS Pro Documentation. Esri. Retrieved 5 January 2023.

[desmith-5] Smith, Michael J.; Goodchild, Michael F.; Longley, Paul A. (2018). "4.4 Distance Operations". Geospatial Analysis: A Comprehensive Guide to Principles, Techniques, and Software Tools (6th ed.).

[6] "25.1.18.81 Voronoi polygons". QGIS 3.22 Documentation. OSGEO. Retrieved 5 January 2023.

[7] "Network Analyst solvers". ArcGIS Pro Documentation. Esri. Retrieved 5 January 2023.

[1]

[2]

[3]

[4]

[5]

[6]

[7]