Reconstruction filter

Last updated

In a mixed-signal system (analog and digital), a reconstruction filter, sometimes called an anti-imaging filter, is used to construct a smooth analog signal from a digital input, as in the case of a digital to analog converter (DAC) or other sampled data output device.

Contents

Sampled data reconstruction filters

The sampling theorem describes why the input of an ADC requires a low-pass analog electronic filter, called the anti-aliasing filter: the sampled input signal must be bandlimited to prevent aliasing (here meaning waves of higher frequency being recorded as a lower frequency).

For the same reason, the output of a DAC requires a low-pass analog filter, called a reconstruction filter - because the output signal must be bandlimited, to prevent imaging (meaning Fourier coefficients being reconstructed as spurious high-frequency 'mirrors'). This is an implementation of the Whittaker–Shannon interpolation formula.

Ideally, both filters should be brickwall filters, constant phase delay in the pass-band with constant flat frequency response, and zero response from the Nyquist frequency. This can be achieved by a filter with a 'sinc' impulse response.

Implementation

While in theory a DAC outputs a series of discrete Dirac impulses, in practice, a real DAC outputs pulses with finite bandwidth and width. Both idealized Dirac pulses, zero-order held steps and other output pulses, if unfiltered, would contain spurious high-frequency replicas, "or images" of the original bandlimited signal. Thus, the reconstruction filter smooths the waveform to remove image frequencies (copies) above the Nyquist limit. In doing so, it reconstructs the continuous time signal (whether originally sampled, or modelled by digital logic) corresponding to the digital time sequence.

Practical filters have non-flat frequency or phase response in the pass band and incomplete suppression of the signal elsewhere. The ideal sinc waveform has an infinite response to a signal, in both the positive and negative time directions, which is impossible to perform in real time – as it would require infinite delay. Consequently, real reconstruction filters typically either allow some energy above the Nyquist rate, attenuate some in-band frequencies, or both. For this reason, oversampling may be used to ensure that frequencies of interest are accurately reproduced without excess energy being emitted out of band.

In systems that have both, the anti-aliasing filter and a reconstruction filter may be of identical design. For example, both the input and the output for audio equipment may be sampled at 44.1 kHz. In this case, both audio filters block as much as possible above 22 kHz and pass as much as possible below 20 kHz.

Alternatively, a system may have no reconstruction filter and simply tolerate some energy being wasted reproducing higher frequency images of the primary signal spectrum.

Image processing

In image processing, digital reconstruction filters are used both to recreate images from samples as in medical imaging [1] and for resampling. [2] A number of comparisons have been made, by various criteria; [1] [2] [3] [4] one observation is that reconstruction can be improved if the derivative of the signal is also known, in addition to the amplitude, [3] and conversely that also performing derivative reconstruction can improve signal reconstruction methods. [1]

Resampling may be referred to as decimation or interpolation, accordingly as the sampling rate decreases or increases – as in sampling and reconstruction generally, the same criteria generally apply in both cases, and thus the same filter can be used.

For resampling, in principle the analog image is reconstructed, then sampled, and this is necessary for general changes in resolution. For integer ratios of sampling rate, one may simplify by sampling the impulse response of the continuous reconstruction filter to produce a discrete resampling filter, then using the discrete resampling filter to directly resample the image. For decimation by an integer amount, only a single sampled filter is necessary; for interpolation by an integer amount, different samplings are needed for different phases – for instance, if one is upsampling by a factor of 4, then one sampled filter is used for the half-way point, while a different sampled filter is used for the point 1/4 of the way from one point to another.

A subtlety in image processing is that (linear) signal processing assumes linear luminance – that doubling a pixel value doubles the luminance of the output. However, images are frequently gamma encoded, notably in the sRGB color space, so luminance is not linear. Thus to apply a linear filter, one must first gamma decode the values – and if resampling, one must gamma decode, resample, then gamma encode.

Common filters

The most common day-to-day filters are: [5]

These are in increasing order of stopband suppression (anti-aliasing), and decreasing speed

For reconstruction purposes, a variety of kernels are used, many of which can be interpreted as approximating the sinc function, [4] either by windowing or by giving a spline approximation, either by cubics or higher order splines. In the case of windowed sinc filters, the frequency response of the reconstruction filter can be understood in terms of the frequency response of the window, as the frequency response of a windowed filter is the convolution of the original response (for sinc, a brick-wall) with the frequency response of the window. Among these, the Lanczos window and Kaiser window are frequently praised.

Another class of reconstruction filters include the Gaussian for various widths, [2] or cardinal B-splines of higher order – the box filter and tent filter being the 0th and 1st order cardinal B-splines. These filters fail to be interpolating filters, since their impulse response do not vanish at all non-zero original sample points – for 1:1 resampling, they are not the identity, but rather blur. On the other hand, being nonnegative, they do not introduce any overshoot or ringing artifacts, and by being wider in the time domain they can be narrower in the frequency domain (by the Fourier uncertainty principle), though at the cost of blurring, which is reflected in passband roll-off ("scalloping").

In photography, a great variety of interpolation filters exist, [6] some proprietary, for which opinions are mixed. Evaluation is often subjective, with reactions being varied, and some arguing that at realistic resampling ratios, there is little difference between them, as compared with bicubic, [7] though for higher resampling ratios behavior is more varied. [8]

Wavelet reconstruction filters

Reconstruction filters are also used when "reconstructing" a waveform or an image from a collection of wavelet coefficients. In medical imaging, a common technique is to use a number of 2D X-ray photos or MRI scans to "reconstruct" a 3D image.

See also

Related Research Articles

<span class="mw-page-title-main">Nyquist–Shannon sampling theorem</span> Sufficiency theorem for reconstructing signals from samples

The Nyquist–Shannon sampling theorem is an essential principle for digital signal processing linking the frequency range of a signal and the sample rate required to avoid a type of distortion called aliasing. The theorem states that the sample rate must be at least twice the bandwidth of the signal to avoid aliasing distortion. In practice, it is used to select band-limiting filters to keep aliasing distortion below an acceptable amount when an analog signal is sampled or when sample rates are changed within a digital signal processing function.

The Whittaker–Shannon interpolation formula or sinc interpolation is a method to construct a continuous-time bandlimited function from a sequence of real numbers. The formula dates back to the works of E. Borel in 1898, and E. T. Whittaker in 1915, and was cited from works of J. M. Whittaker in 1935, and in the formulation of the Nyquist–Shannon sampling theorem by Claude Shannon in 1949. It is also commonly called Shannon's interpolation formula and Whittaker's interpolation formula. E. T. Whittaker, who published it in 1915, called it the Cardinal series.

In digital signal processing, spatial anti-aliasing is a technique for minimizing the distortion artifacts (aliasing) when representing a high-resolution image at a lower resolution. Anti-aliasing is used in digital photography, computer graphics, digital audio, and many other applications.

<span class="mw-page-title-main">Aliasing</span> Signal processing effect

In signal processing and related disciplines, aliasing is the overlapping of frequency components resulting from a sample rate below the Nyquist rate. This overlap results in distortion or artifacts when the signal is reconstructed from samples which causes the reconstructed signal to differ from the original continuous signal. Aliasing that occurs in signals sampled in time, for instance in digital audio or the stroboscopic effect, is referred to as temporal aliasing. Aliasing in spatially sampled signals is referred to as spatial aliasing.

<span class="mw-page-title-main">Sampling (signal processing)</span> Measurement of a signal at discrete time intervals

In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. A common example is the conversion of a sound wave to a sequence of "samples". A sample is a value of the signal at a point in time and/or space; this definition differs from the term's usage in statistics, which refers to a set of such values.

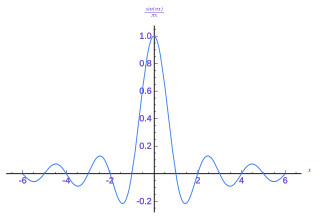
<span class="mw-page-title-main">Sinc filter</span> Ideal low-pass filter or averaging filter

In signal processing, a sinc filter can refer to either a sinc-in-time filter whose impulse response is a sinc function and whose frequency response is rectangular, or to a sinc-in-frequency filter whose impulse response is rectangular and whose frequency response is a sinc function. Calling them according to which domain the filter resembles a sinc avoids confusion. If the domain is unspecified, sinc-in-time is often assumed, or context hopefully can infer the correct domain.

<span class="mw-page-title-main">Undersampling</span> Signal processing sample technique

In signal processing, undersampling or bandpass sampling is a technique where one samples a bandpass-filtered signal at a sample rate below its Nyquist rate, but is still able to reconstruct the signal.

<span class="mw-page-title-main">Bandlimiting</span> Limiting a signal to contain only low-frequency components

Bandlimiting refers to a process which reduces the energy of a signal to an acceptably low level outside of a desired frequency range.

<span class="mw-page-title-main">Direct digital synthesis</span>

Direct digital synthesis (DDS) is a method employed by frequency synthesizers used for creating arbitrary waveforms from a single, fixed-frequency reference clock. DDS is used in applications such as signal generation, local oscillators in communication systems, function generators, mixers, modulators, sound synthesizers and as part of a digital phase-locked loop.

An anti-aliasing filter (AAF) is a filter used before a signal sampler to restrict the bandwidth of a signal to satisfy the Nyquist–Shannon sampling theorem over the band of interest. Since the theorem states that unambiguous reconstruction of the signal from its samples is possible when the power of frequencies above the Nyquist frequency is zero, a brick wall filter is an idealized but impractical AAF. A practical AAF makes a trade off between reduced bandwidth and increased aliasing. A practical anti-aliasing filter will typically permit some aliasing to occur or attenuate or otherwise distort some in-band frequencies close to the Nyquist limit. For this reason, many practical systems sample higher than would be theoretically required by a perfect AAF in order to ensure that all frequencies of interest can be reconstructed, a practice called oversampling.

In signal processing, oversampling is the process of sampling a signal at a sampling frequency significantly higher than the Nyquist rate. Theoretically, a bandwidth-limited signal can be perfectly reconstructed if sampled at the Nyquist rate or above it. The Nyquist rate is defined as twice the bandwidth of the signal. Oversampling is capable of improving resolution and signal-to-noise ratio, and can be helpful in avoiding aliasing and phase distortion by relaxing anti-aliasing filter performance requirements.

<span class="mw-page-title-main">Delta-sigma modulation</span> Method for converting signals between digital and analog

Delta-sigma modulation is an oversampling method for encoding signals into low bit depth digital signals at a very high sample-frequency as part of the process of delta-sigma analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delta-sigma modulation achieves high quality by utilizing a negative feedback loop during quantization to the lower bit depth that continuously corrects quantization errors and moves quantization noise to higher frequencies well above the original signal's bandwidth. Subsequent low-pass filtering for demodulation easily removes this high frequency noise and time averages to achieve high accuracy in amplitude.

<span class="mw-page-title-main">Lanczos resampling</span> Application of a mathematical formula

Lanczos filtering and Lanczos resampling are two applications of a mathematical formula. It can be used as a low-pass filter or used to smoothly interpolate the value of a digital signal between its samples. In the latter case, it maps each sample of the given signal to a translated and scaled copy of the Lanczos kernel, which is a sinc function windowed by the central lobe of a second, longer, sinc function. The sum of these translated and scaled kernels is then evaluated at the desired points.

<span class="mw-page-title-main">Image scaling</span> Changing the resolution of a digital image

In computer graphics and digital imaging, imagescaling refers to the resizing of a digital image. In video technology, the magnification of digital material is known as upscaling or resolution enhancement.

Sample-rate conversion, sampling-frequency conversion or resampling is the process of changing the sampling rate or sampling frequency of a discrete signal to obtain a new discrete representation of the underlying continuous signal. Application areas include image scaling and audio/visual systems, where different sampling rates may be used for engineering, economic, or historical reasons.

The zero-order hold (ZOH) is a mathematical model of the practical signal reconstruction done by a conventional digital-to-analog converter (DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.

First-order hold (FOH) is a mathematical model of the practical reconstruction of sampled signals that could be done by a conventional digital-to-analog converter (DAC) and an analog circuit called an integrator. For FOH, the signal is reconstructed as a piecewise linear approximation to the original signal that was sampled. A mathematical model such as FOH (or, more commonly, the zero-order hold) is necessary because, in the sampling and reconstruction theorem, a sequence of Dirac impulses, xs(t), representing the discrete samples, x(nT), is low-pass filtered to recover the original signal that was sampled, x(t). However, outputting a sequence of Dirac impulses is impractical. Devices can be implemented, using a conventional DAC and some linear analog circuitry, to reconstruct the piecewise linear output for either predictive or delayed FOH.

In electronics and telecommunications, pulse shaping is the process of changing a transmitted pulses' waveform to optimize the signal for its intended purpose or the communication channel. This is often done by limiting the bandwidth of the transmission and filtering the pulses to control intersymbol interference. Pulse shaping is particularly important in RF communication for fitting the signal within a certain frequency band and is typically applied after line coding and modulation.

A Bitcrusher is an audio effect that produces distortion by reducing of the resolution or bandwidth of digital audio data. The resulting quantization noise may produce a "warmer" sound impression, or a harsh one, depending on the amount of reduction.

In digital signal processing, multidimensional sampling is the process of converting a function of a multidimensional variable into a discrete collection of values of the function measured on a discrete set of points. This article presents the basic result due to Petersen and Middleton on conditions for perfectly reconstructing a wavenumber-limited function from its measurements on a discrete lattice of points. This result, also known as the Petersen–Middleton theorem, is a generalization of the Nyquist–Shannon sampling theorem for sampling one-dimensional band-limited functions to higher-dimensional Euclidean spaces.

References

  1. 1 2 3 Theußl, Thomas; Hauser, Helwig; Gröller, Meister Eduard (October 2000). Mastering Windows: Improving Reconstruction (PDF). IEEE/ACM SIGGRAPH Symposium on Volume Visualization. Salt Lake City, Utah, United States. pp. 101–108. doi:10.1109/VV.2000.10002. ISBN   1-58113-308-1. (Project webpage)
  2. 1 2 3 Turkowski, Ken (1990). "Filters for Common Resampling Tasks" (PDF).
  3. 1 2 Mitchell, Don P.; Netravali, Arun N. (August 1988). Reconstruction filters in computer-graphics (PDF). ACM SIGGRAPH International Conference on Computer Graphics and Interactive Techniques. Vol. 22. pp. 221–228. doi:10.1145/54852.378514. ISBN   0-89791-275-6.
  4. 1 2 Meijering, Erik H. W.; Niessen; Pluim; Viergever. Quantitative Comparison of Sinc-Approximating Kernels for Medical Image Interpolation. Medical Image Computing and Computer-Assisted Intervention--MICCAI '99: second international conference, Cambridge, UK, September 19–22, 1999 proceedings.
  5. ↑ dpreview: Interpolation, by Vincent Bockaert
  6. ↑ Digital Photo Interpolation Review
  7. ↑ Interpolation -- Part I, Ron Bigelow
  8. ↑ Image Filter - Sepia
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.