Digital data, in information theory and information systems, is information represented as a string of discrete symbols, each of which can take on one of only a finite number of values from some alphabet, such as letters or digits. An example is a text document, which consists of a string of alphanumeric characters. The most common form of digital data in modern information systems is binary data, which is represented by a string of binary digits (bits) each of which can have one of two values, either 0 or 1.
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor.
In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the carrier signal, with a separate signal called the modulation signal that typically contains information to be transmitted. For example, the modulation signal might be an audio signal representing sound from a microphone, a video signal representing moving images from a video camera, or a digital signal representing a sequence of binary digits, a bitstream from a computer.

Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing signals, such as sound, images, potential fields, seismic signals, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal.

In electronics, an analog-to-digital converter is a system that converts an analog signal, such as a sound picked up by a microphone or light entering a digital camera, into a digital signal. An ADC may also provide an isolated measurement such as an electronic device that converts an analog input voltage or current to a digital number representing the magnitude of the voltage or current. Typically the digital output is a two's complement binary number that is proportional to the input, but there are other possibilities.

The μ-law algorithm is a companding algorithm, primarily used in 8-bit PCM digital telecommunication systems in North America and Japan. It is one of the two companding algorithms in the G.711 standard from ITU-T, the other being the similar A-law. A-law is used in regions where digital telecommunication signals are carried on E-1 circuits, e.g. Europe.

Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to noise power, often expressed in decibels. A ratio higher than 1:1 indicates more signal than noise.

In electronics, a digital-to-analog converter is a system that converts a digital signal into an analog signal. An analog-to-digital converter (ADC) performs the reverse function.

A digital signal processor (DSP) is a specialized microprocessor chip, with its architecture optimized for the operational needs of digital signal processing. DSPs are fabricated on metal–oxide–semiconductor (MOS) integrated circuit chips. They are widely used in audio signal processing, telecommunications, digital image processing, radar, sonar and speech recognition systems, and in common consumer electronic devices such as mobile phones, disk drives and high-definition television (HDTV) products.
Sound can be recorded and stored and played using either digital or analog techniques. Both techniques introduce errors and distortions in the sound, and these methods can be systematically compared. Musicians and listeners have argued over the superiority of digital versus analog sound recordings. Arguments for analog systems include the absence of fundamental error mechanisms which are present in digital audio systems, including aliasing and associated anti-aliasing filter implementation, jitter and quantization noise. Advocates of digital point to the high levels of performance possible with digital audio, including excellent linearity in the audible band and low levels of noise and distortion.

In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. A common example is the conversion of a sound wave to a sequence of "samples". A sample is a value of the signal at a point in time and/or space; this definition differs from the term's usage in statistics, which refers to a set of such values.

Signal refers to both the process and the result of transmission of data over some media accomplished by embedding some variation. Signals are important in multiple subject fields including signal processing, information theory and biology.
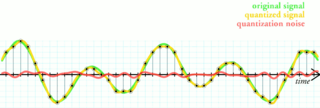
Quantization, in mathematics and digital signal processing, is the process of mapping input values from a large set to output values in a (countable) smaller set, often with a finite number of elements. Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms.
In numerical analysis, computational physics, and simulation, discretization error is the error resulting from the fact that a function of a continuous variable is represented in the computer by a finite number of evaluations, for example, on a lattice. Discretization error can usually be reduced by using a more finely spaced lattice, with an increased computational cost.

Delta-sigma modulation is an oversampling method for encoding signals into low bit depth digital signals at a very high sample-frequency as part of the process of delta-sigma analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delta-sigma modulation achieves high quality by utilizing a negative feedback loop during quantization to the lower bit depth that continuously corrects quantization errors and moves quantization noise to higher frequencies well above the original signal's bandwidth. Subsequent low-pass filtering for demodulation easily removes this high frequency noise and time averages to achieve high accuracy in amplitude which can be ultimately encoded as pulse-code modulation (PCM).

In digital audio using pulse-code modulation (PCM), bit depth is the number of bits of information in each sample, and it directly corresponds to the resolution of each sample. Examples of bit depth include Compact Disc Digital Audio, which uses 16 bits per sample, and DVD-Audio and Blu-ray Disc, which can support up to 24 bits per sample.
A Bitcrusher is an audio effect that produces distortion by reducing the resolution or bandwidth of digital audio data. The resulting quantization noise may produce a "warmer" sound impression, or a harsh one, depending on the amount of reduction.
Pulse-code modulation (PCM) is a method used to digitally represent analog signals. It is the standard form of digital audio in computers, compact discs, digital telephony and other digital audio applications. In a PCM stream, the amplitude of the analog signal is sampled at uniform intervals, and each sample is quantized to the nearest value within a range of digital steps.

A digital signal is a signal that represents data as a sequence of discrete values; at any given time it can only take on, at most, one of a finite number of values. This contrasts with an analog signal, which represents continuous values; at any given time it represents a real number within a continuous range of values.
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which variables that evolve over time are modeled.