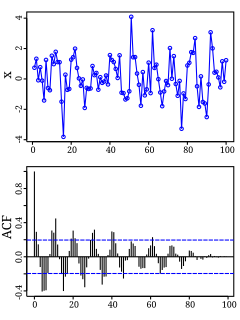
Autocorrelation, also known as serial correlation, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals.
In a chemical reaction, chemical equilibrium is the state in which both reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.
In physics, optical depth or optical thickness is the natural logarithm of the ratio of incident to transmitted radiant power through a material, and spectral optical depth or spectral optical thickness is the natural logarithm of the ratio of incident to transmitted spectral radiant power through a material. Optical depth is dimensionless, and in particular is not a length, though it is a monotonically increasing function of optical path length, and approaches zero as the path length approaches zero. The use of the term "optical density" for optical depth is discouraged.
The phase delay property of a linear time invariant (LTI) system or device such as an amplifier, filter, or telecommunications system, gives the time delay of the various frequency components of a signal to pass through from input to output. In some cases this time delay, as revealed by the phase delay property, will be different for the various frequency components, in which case the signal comprising these signal components will suffer distortion because these components are not delayed by the same amount of time at the output of the device. A sufficiently large time delay variation can cause signal problems such as poor fidelity in video or audio, for example.

The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from zero to one in a very short time. The concept can be extended to the abstract mathematical notion of a dynamical system using an evolution parameter.
In descriptive statistics and chaos theory, a recurrence plot (RP) is a plot showing, for each moment i in time, the times at which a phase space trajectory visits roughly the same area in the phase space as at time j. In other words, it is a graph of
In mathematics and in signal processing, the Hilbert transform is a specific linear operator that takes a function, u(t) of a real variable and produces another function of a real variable H(u)(t). This linear operator is given by convolution with the function :

In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy.
In electronics, when describing a voltage or current step function, rise time is the time taken by a signal to change from a specified low value to a specified high value. These values may be expressed as ratios or, equivalently, as percentages with respect to a given reference value. In analog electronics and digital electronics, these percentages are commonly the 10% and 90% of the output step height: however, other values are commonly used. For applications in control theory, according to Levine, rise time is defined as "the time required for the response to rise from x% to y% of its final value", with 0% to 100% rise time common for underdamped second order systems, 5% to 95% for critically damped and 10% to 90% for overdamped ones. According to Orwiler, the term "rise time" applies to either positive or negative step response, even if a displayed negative excursion is popularly termed fall time.
In system analysis, among other fields of study, a linear time-invariant system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined below. These properties apply to many important physical systems, in which case the response y(t) of the system to an arbitrary input x(t) can be found directly using convolution: y(t) = x(t) * h(t) where h(t) is called the system's impulse response and * represents convolution. What's more, there are systematic methods for solving any such system, whereas systems not meeting both properties are generally more difficult to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers..
Estimation theory is a branch of statistics that deals with estimating the values of parameters based on measured empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the measured data. An estimator attempts to approximate the unknown parameters using the measurements.
Recurrence quantification analysis (RQA) is a method of nonlinear data analysis for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory.
In physics, the Fermi–Pasta–Ulam–Tsingou problem or formerly the Fermi–Pasta–Ulam problem was the apparent paradox in chaos theory that many complicated enough physical systems exhibited almost exactly periodic behavior – called Fermi–Pasta–Ulam–Tsingou recurrence – instead of the expected ergodic behavior. This came as a surprise, as Fermi, certainly, expected the system to thermalize in a fairly short time. That is, it was expected for all vibrational modes to eventually appear with equal strength, as per the equipartition theorem, or, more generally, the ergodic hypothesis. Yet here was a system that appeared to evade the ergodic hypothesis! Although the recurrence is easily observed, it eventually became apparent that over much, much longer time periods, the system does eventually thermalize. Multiple competing theories have been proposed to explain the behavior of the system, and it remains a topic of active research.
A cyclostationary process is a signal having statistical properties that vary cyclically with time. A cyclostationary process can be viewed as multiple interleaved stationary processes. For example, the maximum daily temperature in New York City can be modeled as a cyclostationary process: the maximum temperature on July 21 is statistically different from the temperature on December 20; however, it is a reasonable approximation that the temperature on December 20 of different years has identical statistics. Thus, we can view the random process composed of daily maximum temperatures as 365 interleaved stationary processes, each of which takes on a new value once per year.
Circular convolution, also known as cyclic convolution, is a special case of periodic convolution, which is the convolution of two periodic functions that have the same period. Periodic convolution arises, for example, in the context of the discrete-time Fourier transform (DTFT). In particular, the DTFT of the product of two discrete sequences is the periodic convolution of the DTFTs of the individual sequences. And each DTFT is a periodic summation of a continuous Fourier transform function. Although DTFTs are usually continuous functions of frequency, the concepts of periodic and circular convolution are also directly applicable to discrete sequences of data. In that context, circular convolution plays an important role in maximizing the efficiency of a certain kind of common filtering operation.
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; in particular, every local martingale that is bounded from below is a supermartingale, and every local martingale that is bounded from above is a submartingale; however, in general a local martingale is not a martingale, because its expectation can be distorted by large values of small probability. In particular, a driftless diffusion process is a local martingale, but not necessarily a martingale.
In mathematics — specifically, in stochastic analysis — an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.
In statistical signal processing, the goal of spectral density estimation (SDE) is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities.

A biological neuron model, also known as a spiking neuron model, is a mathematical description of the properties of certain cells in the nervous system that generate sharp electrical potentials across their cell membrane, roughly one millisecond in duration, called action potentials or spikes. Spiking neurons are known to be a major signaling unit of the nervous system, and for this reason characterizing their operation is of great importance. It is worth noting that not all the cells of the nervous system produce the type of spike that define the scope of the spiking neuron models. For example, cochlear hair cells, retinal receptor cells, and retinal bipolar cells do not spike. Furthermore, many cells in the nervous system are not classified as neurons but instead are classified as glia.
In signal processing, nonlinear multidimensional signal processing (NMSP) covers all signal processing using nonlinear multidimensional signals and systems. Nonlinear multidimensional signal processing is a subset of signal processing. Nonlinear multi-dimensional systems can be used in a broad range such as imaging, teletraffic, communications, hydrology, geology, and economics. Nonlinear systems cannot be treated as linear systems, using Fourier transformation and wavelet analysis. Nonlinear systems will have chaotic behavior, limit cycle, steady state, bifurcation, multi-stability and so on. Nonlinear systems do not have a canonical representation, like impulse response for linear systems. But there are some efforts to characterize nonlinear systems, such as Volterra and Wiener series using polynomial integrals as the use of those methods naturally extend the signal into multi-dimensions. Another example is the Empirical mode decomposition method using Hilbert transform instead of Fourier Transform for nonlinear multi-dimensional systems. This method is an empirical method and can be directly applied to data sets. Multi-dimensional nonlinear filters (MDNF) are also an important part of NMSP, MDNF are mainly used to filter noise in real data. There are nonlinear-type hybrid filters used in color image processing, nonlinear edge-preserving filters use in magnetic resonance image restoration. Those filters use both temporal and spatial information and combine the maximum likelihood estimate with the spatial smoothing algorithm.
















