A context-sensitive grammar (CSG) is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols. Context-sensitive grammars are more general than context-free grammars, in the sense that there are languages that can be described by CSG but not by context-free grammars. Context-sensitive grammars are less general than unrestricted grammars. Thus, CSG are positioned between context-free and unrestricted grammars in the Chomsky hierarchy.
In formal language theory, a context-free grammar (CFG) is a certain type of formal grammar: a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the rule
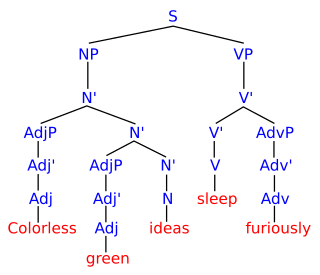
In mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules.

In theoretical computer science and mathematics, the theory of computation is the branch that deals with how efficiently problems can be solved on a model of computation, using an algorithm. The field is divided into three major branches: automata theory and languages, computability theory, and computational complexity theory, which are linked by the question: "What are the fundamental capabilities and limitations of computers?".
In formal language theory, a context-free grammar is in Greibach normal form (GNF) if the right-hand sides of all production rules start with a terminal symbol, optionally followed by some variables. A non-strict form allows one exception to this format restriction for allowing the empty word to be a member of the described language. The normal form was established by Sheila Greibach and it bears her name.
In computer science, a recursive descent parser is a kind of top-down parser built from a set of mutually recursive procedures where each such procedure implements one of the nonterminals of the grammar. Thus the structure of the resulting program closely mirrors that of the grammar it recognizes.
In computer science, top-down parsing is a parsing strategy where one first looks at the highest level of the parse tree and works down the parse tree by using the rewriting rules of a formal grammar. LL parsers are a type of parser that uses a top-down parsing strategy.
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science. The computability of a problem is closely linked to the existence of an algorithm to solve the problem.
Tree-adjoining grammar (TAG) is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol. Whereas context-free grammars have rules for rewriting symbols as strings of other symbols, tree-adjoining grammars have rules for rewriting the nodes of trees as other trees.
In computing, memoization or memoisation is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again. Memoization has also been used in other contexts, such as in simple mutually recursive descent parsing. Although related to caching, memoization refers to a specific case of this optimization, distinguishing it from forms of caching such as buffering or page replacement. In the context of some logic programming languages, memoization is also known as tabling; see also lookup table.
Top-Down Parsing Language (TDPL) is a type of analytic formal grammar developed by Alexander Birman in the early 1970s in order to study formally the behavior of a common class of practical top-down parsers that support a limited form of backtracking. Birman originally named his formalism the TMG Schema (TS), after TMG, an early parser generator, but the formalism was later given the name TDPL by Aho and Ullman in their classic anthology The Theory of Parsing, Translation and Compiling.
In computer science, a parsing expression grammar, or PEG, is a type of analytic formal grammar, i.e. it describes a formal language in terms of a set of rules for recognizing strings in the language. The formalism was introduced by Bryan Ford in 2004 and is closely related to the family of top-down parsing languages introduced in the early 1970s. Syntactically, PEGs also look similar to context-free grammars (CFGs), but they have a different interpretation: the choice operator selects the first match in PEG, while it is ambiguous in CFG. This is closer to how string recognition tends to be done in practice, e.g. by a recursive descent parser.

Grammar induction is the process in machine learning of learning a formal grammar from a set of observations, thus constructing a model which accounts for the characteristics of the observed objects. More generally, grammatical inference is that branch of machine learning where the instance space consists of discrete combinatorial objects such as strings, trees and graphs.
In computer science, terminal and nonterminal symbols are the lexical elements used in specifying the production rules constituting a formal grammar. Terminal symbols are the elementary symbols of the language defined by a formal grammar. Nonterminal symbols are replaced by groups of terminal symbols according to the production rules.
In computer programming, a parser combinator is a higher-order function that accepts several parsers as input and returns a new parser as its output. In this context, a parser is a function accepting strings as input and returning some structure as output, typically a parse tree or a set of indices representing locations in the string where parsing stopped successfully. Parser combinators enable a recursive descent parsing strategy that facilitates modular piecewise construction and testing. This parsing technique is called combinatory parsing.
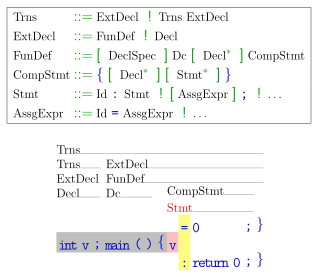
In formal language theory, an LL grammar is a context-free grammar that can be parsed by an LL parser, which parses the input from Left to right, and constructs a Leftmost derivation of the sentence. A language that has an LL grammar is known as an LL language. These form subsets of deterministic context-free grammars (DCFGs) and deterministic context-free languages (DCFLs), respectively. One says that a given grammar or language "is an LL grammar/language" or simply "is LL" to indicate that it is in this class.






