Rota's conjecture

Last updated

Rota's excluded minors conjecture is one of a number of conjectures made by the mathematician Gian-Carlo Rota. It is considered an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. [1] A proof of the conjecture was announced, but not published, in 2014 by Geelen, Gerards, and Whittle. [2]

Contents

Statement of the conjecture

If is a set of points in a vector space defined over a field , then the linearly independent subsets of form the independent sets of a matroid ; is said to be a representation of any matroid isomorphic to . Not every matroid has a representation over every field, for instance, the Fano plane is representable only over fields of characteristic two. Other matroids are representable over no fields at all. The matroids that are representable over a particular field form a proper subclass of all matroids.

A minor of a matroid is another matroid formed by a sequence of two operations: deletion and contraction. In the case of points from a vector space, deleting a point is simply the removal of that point from ; contraction is a dual operation in which a point is removed and the remaining points are projected a hyperplane that does not contain the removed points. It follows from this if a matroid is representable over a field, then so are all its minors. A matroid that is not representable over , and is minor-minimal with that property, is called an "excluded minor"; a matroid is representable over if and only if it does not contain one of the forbidden minors.

For representability over the real numbers, there are infinitely many forbidden minors. [3] Rota's conjecture is that, for every finite field , there is only a finite number of forbidden minors.

Partial results

W. T. Tutte proved that the binary matroids (matroids representable over the field of two elements) have a single forbidden minor, the uniform matroid (geometrically, a line with four points on it). [4] [5]

A matroid is representable over the ternary field GF(3) if and only if it does not have one or more of the following four matroids as minors: a five-point line , its dual matroid (five points in general position in three dimensions), the Fano plane, or the dual of the Fano plane. Thus, Rota's conjecture is true in this case as well. [6] [7] As a consequence of this result and of the forbidden minor characterization by Tutte (1958) of the regular matroids (matroids that can be represented over all fields) it follows that a matroid is regular if and only if it is both binary and ternary. [7]

There are seven forbidden minors for the matroids representable over GF(4). [8] They are:

This result won the 2003 Fulkerson Prize for its authors Jim Geelen, A. M. H. Gerards, and A. Kapoor. [10]

For GF(5), several forbidden minors on up to 12 elements are known, [11] but it is not known whether the list is complete.

Reported proof

Geoff Whittle announced during a 2013 visit to the UK that he, Jim Geelen, and Bert Gerards had solved Rota's conjecture. The collaboration involved intense visits where the researchers sat in a room together, all day every day, in front of a whiteboard. [12] It would take them years to write up their research in its entirety and publish it. [13] [14] An outline of the proof appeared 2014 in the Notices of the American Mathematical Society. [15] Only one paper by the same authors, related to this conjecture, has subsequently appeared. [16]

See also

Related Research Articles

<span class="mw-page-title-main">Projective plane</span> Geometric concept of a 2D space with a "point at infinity" adjoined

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect at a single point, but there are some pairs of lines that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two distinct lines in a projective plane intersect at exactly one point.

In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.

In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges, vertices and by contracting edges.

In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

<span class="mw-page-title-main">Sylvester–Gallai theorem</span> Existence of a line through two points

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.

The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

In mathematics, a regular matroid is a matroid that can be represented over all fields.

<span class="mw-page-title-main">Branch-decomposition</span> Hierarchical clustering of graph edges

In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

In matroid theory, the dual of a matroid is another matroid that has the same elements as , and in which a set is independent if and only if has a basis set disjoint from it.

<span class="mw-page-title-main">Oriented matroid</span> Abstraction of ordered linear algebra

An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.

Jim Geelen is a professor at the Department of Combinatorics and Optimization in the faculty of mathematics at the University of Waterloo, where he holds the Canada Research Chair in Combinatorial optimization. He is known for his work on Matroid theory and the extension of the Graph Minors Project to representable matroids. In 2003, he won the Fulkerson Prize with his co-authors A. M. H. Gerards, and A. Kapoor for their research on Rota's excluded minors conjecture. In 2006, he won the Coxeter–James Prize presented by the Canadian Mathematical Society.

In matroid theory, a field within mathematics, a gammoid is a certain kind of matroid, describing sets of vertices that can be reached by vertex-disjoint paths in a directed graph.

In mathematics, a uniform matroid is a matroid in which the independent sets are exactly the sets containing at most r elements, for some fixed integer r. An alternative definition is that every permutation of the elements is a symmetry.

In the mathematical theory of matroids, a minor of a matroid M is another matroid N that is obtained from M by a sequence of restriction and contraction operations. Matroid minors are closely related to graph minors, and the restriction and contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to structural decompositions of matroids, and characterizations of matroid families by forbidden minors, analogous to the corresponding theory in graphs.

In matroid theory, a binary matroid is a matroid that can be represented over the finite field GF(2). That is, up to isomorphism, they are the matroids whose elements are the columns of a (0,1)-matrix and whose sets of elements are independent if and only if the corresponding columns are linearly independent in GF(2).

In matroid theory, an Eulerian matroid is a matroid whose elements can be partitioned into a collection of disjoint circuits.

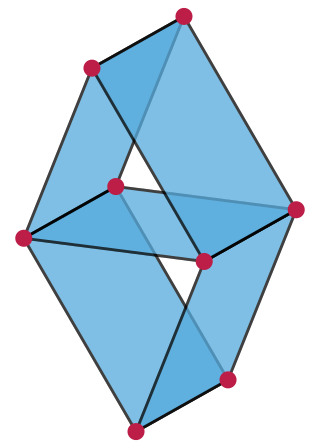
<span class="mw-page-title-main">Vámos matroid</span> Matroid with no linear representation

In mathematics, the Vámos matroid or Vámos cube is a matroid over a set of eight elements that cannot be represented as a matrix over any field. It is named after English mathematician Peter Vámos, who first described it in an unpublished manuscript in 1968.

In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.

<span class="mw-page-title-main">Paving matroid</span> Matroid without short circuits

In the mathematical theory of matroids, a paving matroid is a matroid in which every circuit has size at least as large as the matroid's rank. In a matroid of rank every circuit has size at most , so it is equivalent to define paving matroids as the matroids in which the size of every circuit belongs to the set . It has been conjectured that almost all matroids are paving matroids.

In linear algebra and matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of bases, named after Gian-Carlo Rota. It states that, if X is either a vector space of dimension n or more generally a matroid of rank n, with n disjoint bases Bi, then it is possible to arrange the elements of these bases into an n × n matrix in such a way that the rows of the matrix are exactly the given bases and the columns of the matrix are also bases. That is, it should be possible to find a second set of n disjoint bases Ci, each of which consists of one element from each of the bases Bi.

References

  1. ↑ Rota, Gian-Carlo (1971), "Combinatorial theory, old and new", Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 3, Paris: Gauthier-Villars, pp. 229–233, MR   0505646 .
  2. ↑ "Solving Rota's conjecture" (PDF), Notices of the American Mathematical Society: 736–743, Aug 17, 2014
  3. ↑ Vámos, P. (1978), "The missing axiom of matroid theory is lost forever", Journal of the London Mathematical Society , Second Series, 18 (3): 403–408, doi:10.1112/jlms/s2-18.3.403, MR   0518224 .
  4. ↑ Tutte, W. T. (1958), "A homotopy theorem for matroids. I, II", Transactions of the American Mathematical Society , 88: 144–174, doi:10.2307/1993244, MR   0101526 .
  5. ↑ Tutte, W. T. (1965), "Lectures on matroids", Journal of Research of the National Bureau of Standards, 69B: 1–47, doi: 10.6028/jres.069b.001 , MR   0179781 . See in particular section 5.3, "Characterization of binary matroids", p.17.
  6. ↑ Bixby, Robert E. (1979), "On Reid's characterization of the ternary matroids", Journal of Combinatorial Theory , Series B, 26 (2): 174–204, doi: 10.1016/0095-8956(79)90056-X , MR   0532587 . Bixby attributes this characterization of ternary matroids to Ralph Reid.
  7. 1 2 Seymour, P. D. (1979), "Matroid representation over GF(3)", Journal of Combinatorial Theory , Series B, 26 (2): 159–173, doi: 10.1016/0095-8956(79)90055-8 , MR   0532586 .
  8. ↑ Geelen, J. F.; Gerards, A. M. H.; Kapoor, A. (2000), "The excluded minors for GF(4)-representable matroids" (PDF), Journal of Combinatorial Theory , Series B, 79 (2): 247–299, doi:10.1006/jctb.2000.1963, MR   1769191, archived from the original (PDF) on 2010-09-24.
  9. ↑ Kelly, L. M.; Moser, W. O. J. (1958), "On the number of ordinary lines determined by n points", Can. J. Math., 10: 210–219, doi: 10.4153/CJM-1958-024-6 .
  10. ↑ 2003 Fulkerson Prize citation, retrieved 2012-08-18.
  11. ↑ Betten, A.; Kingan, R. J.; Kingan, S. R. (2007), "A note on GF(5)-representable matroids" (PDF), MATCH Communications in Mathematical and in Computer Chemistry, 58 (2): 511–521, MR   2357372 .
  12. ↑ Geelen, Gerards and Whittle announce a proof of Rota's conjecture University of Waterloo, August 28, 2013
  13. ↑ Rota's Conjecture: Researcher solves 40-year-old math problem PhysOrg, August 15, 2013.
  14. ↑ CWI researcher proves famous Rota’s Conjecture Archived 2013-10-26 at the Wayback Machine CWI, August 22, 2013.
  15. ↑ "Solving Rota's conjecture" (PDF), Notices of the American Mathematical Society: 736–743, Aug 17, 2014
  16. ↑ Geelen, Jim; Gerards, Bert; Whittle, Geoff (2015), "The highly connected matroids in minor-closed classes", Annals of Combinatorics, 19 (1): 107–123, arXiv: 1312.5012 , doi:10.1007/s00026-015-0251-3, MR   3319863
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.