
A composite material is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a material with properties unlike the individual elements. Within the finished structure, the individual elements remain separate and distinct, distinguishing composites from mixtures and solid solutions.

In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to tensile stress and may undergo elongation. An object being pushed together, such as a crumpled sponge, is subject to compressive stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has dimension of force per area, with SI units of newtons per square meter (N/m2) or pascal (Pa).

In engineering and materials science, a stress–strain curve for a material gives the relationship between stress and strain. It is obtained by gradually applying load to a test coupon and measuring the deformation, from which the stress and strain can be determined. These curves reveal many of the properties of a material, such as the Young's modulus, the yield strength and the ultimate tensile strength.
Dynamic mechanical analysis is a technique used to study and characterize materials. It is most useful for studying the viscoelastic behavior of polymers. A sinusoidal stress is applied and the strain in the material is measured, allowing one to determine the complex modulus. The temperature of the sample or the frequency of the stress are often varied, leading to variations in the complex modulus; this approach can be used to locate the glass transition temperature of the material, as well as to identify transitions corresponding to other molecular motions.
The field of strength of materials typically refers to various methods of calculating the stresses and strains in structural members, such as beams, columns, and shafts. The methods employed to predict the response of a structure under loading and its susceptibility to various failure modes takes into account the properties of the materials such as its yield strength, ultimate strength, Young's modulus, and Poisson's ratio. In addition, the mechanical element's macroscopic properties such as its length, width, thickness, boundary constraints and abrupt changes in geometry such as holes are considered.

In mechanics, compressive strength is the capacity of a material or structure to withstand loads tending to reduce size. In other words, compressive strength resists compression, whereas tensile strength resists tension. In the study of strength of materials, tensile strength, compressive strength, and shear strength can be analyzed independently.

Shear stress is the component of stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. Normal stress, on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts.
Stress–strain analysis is an engineering discipline that uses many methods to determine the stresses and strains in materials and structures subjected to forces. In continuum mechanics, stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material.
In continuum mechanics, the maximum distortion energy criterion states that yielding of a ductile material begins when the second invariant of deviatoric stress reaches a critical value. It is a part of plasticity theory that mostly applies to ductile materials, such as some metals. Prior to yield, material response can be assumed to be of a nonlinear elastic, viscoelastic, or linear elastic behavior.
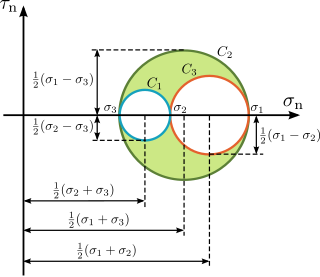
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor.

In materials science, work hardening, also known as strain hardening, is the strengthening of a metal or polymer by plastic deformation. Work hardening may be desirable, undesirable, or inconsequential, depending on the context.

In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation.

In materials science, critical resolved shear stress (CRSS) is the component of shear stress, resolved in the direction of slip, necessary to initiate slip in a grain. Resolved shear stress (RSS) is the shear component of an applied tensile or compressive stress resolved along a slip plane that is other than perpendicular or parallel to the stress axis. The RSS is related to the applied stress by a geometrical factor, m, typically the Schmid factor:

Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the stress in a material just before it yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol .
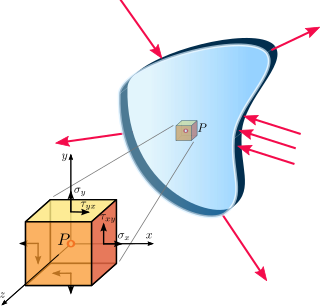
In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2. A related notion, plane strain, is often applicable to very thick members.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.
Material failure theory is an interdisciplinary field of materials science and solid mechanics which attempts to predict the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure (fracture) or ductile failure (yield). Depending on the conditions most materials can fail in a brittle or ductile manner or both. However, for most practical situations, a material may be classified as either brittle or ductile.

A fiber-reinforced composite (FRC) is a composite building material that consists of three components:
- the fibers as the discontinuous or dispersed phase,
- the matrix as the continuous phase, and
- the fine interphase region, also known as the interface.
The four-point flexural test provides values for the modulus of elasticity in bending , flexural stress , flexural strain and the flexural stress-strain response of the material. This test is very similar to the three-point bending flexural test. The major difference being that with the addition of a fourth bearing the portion of the beam between the two loading points is put under maximum stress, as opposed to only the material right under the central bearing in the case of three-point bending.
The unified strength theory (UST). proposed by Yu Mao-Hong is a series of yield criteria and failure criteria. It is a generalized classical strength theory which can be used to describe the yielding or failure of material begins when the combination of principal stresses reaches a critical value.
























