Strength of materials

The field of strength of materials (also called mechanics of materials) typically refers to various methods of calculating the stresses and strains in structural members, such as beams, columns, and shafts. The methods employed to predict the response of a structure under loading and its susceptibility to various failure modes takes into account the properties of the materials such as its yield strength, ultimate strength, Young's modulus, and Poisson's ratio. In addition, the mechanical element's macroscopic properties (geometric properties) such as its length, width, thickness, boundary constraints and abrupt changes in geometry such as holes are considered.

The theory began with the consideration of the behavior of one and two dimensional members of structures, whose states of stress can be approximated as two dimensional, and was then generalized to three dimensions to develop a more complete theory of the elastic and plastic behavior of materials. An important founding pioneer in mechanics of materials was Stephen Timoshenko.

Definition

In the mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. The field of strength of materials deals with forces and deformations that result from their acting on a material. A load applied to a mechanical member will induce internal forces within the member called stresses when those forces are expressed on a unit basis. The stresses acting on the material cause deformation of the material in various manners including breaking them completely. Deformation of the material is called strain when those deformations too are placed on a unit basis.

The stresses and strains that develop within a mechanical member must be calculated in order to assess the load capacity of that member. This requires a complete description of the geometry of the member, its constraints, the loads applied to the member and the properties of the material of which the member is composed. The applied loads may be axial (tensile or compressive), or rotational (strength shear). With a complete description of the loading and the geometry of the member, the state of stress and state of strain at any point within the member can be calculated. Once the state of stress and strain within the member is known, the strength (load carrying capacity) of that member, its deformations (stiffness qualities), and its stability (ability to maintain its original configuration) can be calculated.

The calculated stresses may then be compared to some measure of the strength of the member such as its material yield or ultimate strength. The calculated deflection of the member may be compared to deflection criteria that are based on the member's use. The calculated buckling load of the member may be compared to the applied load. The calculated stiffness and mass distribution of the member may be used to calculate the member's dynamic response and then compared to the acoustic environment in which it will be used.

Material strength refers to the point on the engineering stress–strain curve (yield stress) beyond which the material experiences deformations that will not be completely reversed upon removal of the loading and as a result, the member will have a permanent deflection. The ultimate strength of the material refers to the maximum value of stress reached. The fracture strength is the stress value at fracture (the last stress value recorded).

Types of loadings

• Transverse loadings – Forces applied perpendicular to the longitudinal axis of a member. Transverse loading causes the member to bend and deflect from its original position, with internal tensile and compressive strains accompanying the change in curvature of the member. ^[1] Transverse loading also induces shear forces that cause shear deformation of the material and increase the transverse deflection of the member.
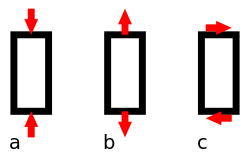
• Axial loading – The applied forces are collinear with the longitudinal axis of the member. The forces cause the member to either stretch or shorten. ^[2]
• Torsional loading – Twisting action caused by a pair of externally applied equal and oppositely directed force couples acting on parallel planes or by a single external couple applied to a member that has one end fixed against rotation.

Stress terms

A material being loaded in a) compression, b) tension, c) shear

Uniaxial stress is expressed by

${\displaystyle \sigma ={\frac {F}{A}},}$

where F is the force acting on an area A. ^[3] The area can be the undeformed area or the deformed area, depending on whether engineering stress or true stress is of interest.

• Compressive stress (or compression) is the stress state caused by an applied load that acts to reduce the length of the material (compression member) along the axis of the applied load; it is, in other words, a stress state that causes a squeezing of the material. A simple case of compression is the uniaxial compression induced by the action of opposite, pushing forces. Compressive strength for materials is generally higher than their tensile strength. However, structures loaded in compression are subject to additional failure modes, such as buckling, that are dependent on the member's geometry.
• Tensile stress is the stress state caused by an applied load that tends to elongate the material along the axis of the applied load, in other words, the stress caused by pulling the material. The strength of structures of equal cross-sectional area loaded in tension is independent of shape of the cross-section. Materials loaded in tension are susceptible to stress concentrations such as material defects or abrupt changes in geometry. However, materials exhibiting ductile behaviour (many metals for example) can tolerate some defects while brittle materials (such as ceramics and some steels) can fail well below their ultimate material strength.
• Shear stress is the stress state caused by the combined energy of a pair of opposing forces acting along parallel lines of action through the material, in other words, the stress caused by faces of the material sliding relative to one another. An example is cutting paper with scissors ^[4] or stresses due to torsional loading.

Stress parameters for resistance

Material resistance can be expressed in several mechanical stress parameters. The term material strength is used when referring to mechanical stress parameters. These are physical quantities with dimension homogeneous to pressure and force per unit surface. The traditional measure unit for strength are therefore MPa in the International System of Units, and the psi between the United States customary units. Strength parameters include: yield strength, tensile strength, fatigue strength, crack resistance, and other parameters.^{[ citation needed ]}

• Yield strength is the lowest stress that produces a permanent deformation in a material. In some materials, like aluminium alloys, the point of yielding is difficult to identify, thus it is usually defined as the stress required to cause 0.2% plastic strain. This is called a 0.2% proof stress. ^[5]

• Compressive strength is a limit state of compressive stress that leads to failure in a material in the manner of ductile failure (infinite theoretical yield) or brittle failure (rupture as the result of crack propagation, or sliding along a weak plane – see shear strength).
• Tensile strength or ultimate tensile strength is a limit state of tensile stress that leads to tensile failure in the manner of ductile failure (yield as the first stage of that failure, some hardening in the second stage and breakage after a possible "neck" formation) or brittle failure (sudden breaking in two or more pieces at a low-stress state). The tensile strength can be quoted as either true stress or engineering stress, but engineering stress is the most commonly used.
• Fatigue strength is a more complex measure of the strength of a material that considers several loading episodes in the service period of an object, ^[6] and is usually more difficult to assess than the static strength measures. Fatigue strength is quoted here as a simple range (${\displaystyle \Delta \sigma =\sigma _{\mathrm {max} }-\sigma _{\mathrm {min} }}$). In the case of cyclic loading it can be appropriately expressed as an amplitude usually at zero mean stress, along with the number of cycles to failure under that condition of stress.

• Impact strength is the capability of the material to withstand a suddenly applied load and is expressed in terms of energy. Often measured with the Izod impact strength test or Charpy impact test, both of which measure the impact energy required to fracture a sample. Volume, modulus of elasticity, distribution of forces, and yield strength affect the impact strength of a material. In order for a material or object to have a high impact strength, the stresses must be distributed evenly throughout the object. It also must have a large volume with a low modulus of elasticity and a high material yield strength. ^[7]

Strain parameters for resistance

• Deformation of the material is the change in geometry created when stress is applied (as a result of applied forces, gravitational fields, accelerations, thermal expansion, etc.). Deformation is expressed by the displacement field of the material. ^[8]
• Strain , or reduced deformation, is a mathematical term that expresses the trend of the deformation change among the material field. Strain is the deformation per unit length. ^[9] In the case of uniaxial loading the displacement of a specimen (for example, a bar element) lead to a calculation of strain expressed as the quotient of the displacement and the original length of the specimen. For 3D displacement fields it is expressed as derivatives of displacement functions in terms of a second-order tensor (with 6 independent elements).
• Deflection is a term to describe the magnitude to which a structural element is displaced when subject to an applied load. ^[10]

Stress–strain relations

Main article: Stress–strain curve

Basic static response of a specimen under tension

• Elasticity is the ability of a material to return to its previous shape after stress is released. In many materials, the relation between applied stress is directly proportional to the resulting strain (up to a certain limit), and a graph representing those two quantities is a straight line.

The slope of this line is known as Young's modulus, or the "modulus of elasticity". The modulus of elasticity can be used to determine the stress–strain relationship in the linear-elastic portion of the stress–strain curve. The linear-elastic region is either below the yield point, or if a yield point is not easily identified on the stress–strain plot it is defined to be between 0 and 0.2% strain, and is defined as the region of strain in which no yielding (permanent deformation) occurs. ^[11]

• Plasticity or plastic deformation is the opposite of elastic deformation and is defined as unrecoverable strain. Plastic deformation is retained after the release of the applied stress. Most materials in the linear-elastic category are usually capable of plastic deformation. Brittle materials, like ceramics, do not experience any plastic deformation and will fracture under relatively low strain, while ductile materials such as metallics, lead, or polymers will plastically deform much more before a fracture initiation.

Consider the difference between a carrot and chewed bubble gum. The carrot will stretch very little before breaking. The chewed bubble gum, on the other hand, will plastically deform enormously before finally breaking.

Design terms

Ultimate strength is an attribute related to a material, rather than just a specific specimen made of the material, and as such it is quoted as the force per unit of cross section area (N/m²). The ultimate strength is the maximum stress that a material can withstand before it breaks or weakens. ^[12] For example, the ultimate tensile strength (UTS) of AISI 1018 Steel is 440 MPa. In Imperial units, the unit of stress is given as lbf/in² or pounds-force per square inch. This unit is often abbreviated as psi. One thousand psi is abbreviated ksi.

A factor of safety is a design criteria that an engineered component or structure must achieve. ${\displaystyle FS=F/f}$, where FS: the factor of safety, Rf The applied stress, and F: ultimate allowable stress (psi or MPa) ^[13]

Margin of Safety is the common method for design criteria. It is defined MS = P_u/P − 1.

For example, to achieve a factor of safety of 4, the allowable stress in an AISI 1018 steel component can be calculated to be ${\displaystyle F=UTS/FS}$ = 440/4 = 110 MPa, or ${\displaystyle F}$ = 110×10⁶ N/m². Such allowable stresses are also known as "design stresses" or "working stresses".

Design stresses that have been determined from the ultimate or yield point values of the materials give safe and reliable results only for the case of static loading. Many machine parts fail when subjected to a non-steady and continuously varying loads even though the developed stresses are below the yield point. Such failures are called fatigue failure. The failure is by a fracture that appears to be brittle with little or no visible evidence of yielding. However, when the stress is kept below "fatigue stress" or "endurance limit stress", the part will endure indefinitely. A purely reversing or cyclic stress is one that alternates between equal positive and negative peak stresses during each cycle of operation. In a purely cyclic stress, the average stress is zero. When a part is subjected to a cyclic stress, also known as stress range (Sr), it has been observed that the failure of the part occurs after a number of stress reversals (N) even if the magnitude of the stress range is below the material's yield strength. Generally, higher the range stress, the fewer the number of reversals needed for failure.

Failure theories

Main article: Material failure theory

There are four failure theories: maximum shear stress theory, maximum normal stress theory, maximum strain energy theory, and maximum distortion energy theory (von Mises criterion of failre). Out of these four theories of failure, the maximum normal stress theory is only applicable for brittle materials, and the remaining three theories are applicable for ductile materials. Of the latter three, the distortion energy theory provides the most accurate results in a majority of the stress conditions. The strain energy theory needs the value of Poisson's ratio of the part material, which is often not readily available. The maximum shear stress theory is conservative. For simple unidirectional normal stresses all theories are equivalent, which means all theories will give the same result.

• Maximum shear stress theory postulates that failure will occur if the magnitude of the maximum shear stress in the part exceeds the shear strength of the material determined from uniaxial testing.
• Maximum normal stress theory postulates that failure will occur if the maximum normal stress in the part exceeds the ultimate tensile stress of the material as determined from uniaxial testing. This theory deals with brittle materials only. The maximum tensile stress should be less than or equal to ultimate tensile stress divided by factor of safety. The magnitude of the maximum compressive stress should be less than ultimate compressive stress divided by factor of safety.
• Maximum strain energy theory postulates that failure will occur when the strain energy per unit volume due to the applied stresses in a part equals the strain energy per unit volume at the yield point in uniaxial testing.
• Maximum distortion energy theory, also known as maximum distortion energy theory of failure or von Mises–Hencky theory. This theory postulates that failure will occur when the distortion energy per unit volume due to the applied stresses in a part equals the distortion energy per unit volume at the yield point in uniaxial testing. The total elastic energy due to strain can be divided into two parts: one part causes change in volume, and the other part causes a change in shape. Distortion energy is the amount of energy that is needed to change the shape.
• Fracture mechanics was established by Alan Arnold Griffith and George Rankine Irwin. This important theory is also known as numeric conversion of toughness of material in the case of crack existence.

A material's strength is dependent on its microstructure. The engineering processes to which a material is subjected can alter this microstructure. The variety of strengthening mechanisms that alter the strength of a material includes work hardening, solid solution strengthening, precipitation hardening, and grain boundary strengthening and can be quantitatively and qualitatively explained. Strengthening mechanisms are accompanied by the caveat that some other mechanical properties of the material may degenerate in an attempt to make the material stronger. For example, in grain boundary strengthening, although yield strength is maximized with decreasing grain size, ultimately, very small grain sizes make the material brittle. In general, the yield strength of a material is an adequate indicator of the material's mechanical strength. Considered in tandem with the fact that the yield strength is the parameter that predicts plastic deformation in the material, one can make informed decisions on how to increase the strength of a material depending on its microstructural properties and the desired end effect. Strength is expressed in terms of the limiting values of the compressive stress, tensile stress, and shear stresses that would cause failure. The effects of dynamic loading are probably the most important practical consideration of the theory of elasticity, especially the problem of fatigue. Repeated loading often initiates cracks, which grow until failure occurs at the corresponding residual strength of the structure. Cracks always start at a stress concentrations especially changes in cross-section of the product or defects in manufacturing, near holes and corners at nominal stress levels far lower than those quoted for the strength of the material.

See also

• Creep (deformation)  – Tendency of a solid material to move slowly or deform permanently under mechanical stress
• Deformation mechanism map  – Microscopic processes responsible for changes in a material's structure, shape and volumePages displaying short descriptions of redirect targets
• Dynamics  – Description of large objects' physicsPages displaying short descriptions of redirect targets
• Fatigue (material)  – Initiation and propagation of cracks in a material due to cyclic loading
• Forensic engineering  – Investigation of failures associated with legal intervention
• Fracture mechanics  – Study of propagation of cracks in materials
• Fracture toughness  – Stress intensity factor at which a crack's propagation increases drastically
• List of materials properties § Mechanical properties
• Material selection  – Step in the process of designing physical objects
• Molecular diffusion  – Thermal motion of liquid or gas particles at temperatures above absolute zero
• Specific strength  – Ratio of strength to mass for a material
• Statics  – Branch of mechanics concerned with balance of forces in nonmoving systems
• Universal testing machine  – Type of equipment for determining tensile or compressive strength of a material

References

1. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. p. 210. ISBN   978-0-07-352938-7.
2. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. p. 7. ISBN   978-0-07-352938-7.
3. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. p. 5. ISBN   978-0-07-352938-7.
4. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 9–10. ISBN   978-0-07-352938-7.
5. Beer, Ferdinand Pierre; Johnston, Elwood Russell; Dewolf, John T (2009). Mechanics of Materials (5th ed.). p. 52. ISBN   978-0-07-352938-7.
6. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. p. 60. ISBN   978-0-07-352938-7.
7. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 693–696. ISBN   978-0-07-352938-7.
8. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. p. 47. ISBN   978-0-07-352938-7.
9. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. p. 49. ISBN   978-0-07-352938-7.
10. R. C. Hibbeler (2009). Structural Analysis (7 ed.). Pearson Prentice Hall. p. 305. ISBN   978-0-13-602060-8.
11. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 53–56. ISBN   978-0-07-352938-7.
12. Beer & Johnston (2006). Mechanics of Materials (5thv ed.). McGraw Hill. pp. 27–28. ISBN   978-0-07-352938-7.
13. Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. p. 28. ISBN   978-0-07-352938-7.

Further reading

• Fa-Hwa Cheng, Initials. (1997). Strength of material. Ohio: McGraw-Hill
• Mechanics of Materials, E.J. Hearn
• Alfirević, Ivo. Strength of Materials I. Tehnička knjiga, 1995. ISBN   953-172-010-X.
• Alfirević, Ivo. Strength of Materials II. Tehnička knjiga, 1999. ISBN   953-6168-85-5.
• Ashby, M.F. Materials Selection in Design. Pergamon, 1992.
• Beer, F.P., E.R. Johnston, et al. Mechanics of Materials, 3rd edition. McGraw-Hill, 2001. ISBN   0-07-248673-2
• Cottrell, A.H. Mechanical Properties of Matter. Wiley, New York, 1964.
• Den Hartog, Jacob P. Strength of Materials. Dover Publications, Inc., 1961, ISBN   0-486-60755-0.
• Drucker, D.C. Introduction to Mechanics of Deformable Solids. McGraw-Hill, 1967.
• Gordon, J.E. The New Science of Strong Materials. Princeton, 1984.
• Groover, Mikell P. Fundamentals of Modern Manufacturing, 2nd edition. John Wiley & Sons, Inc., 2002. ISBN   0-471-40051-3.
• Hashemi, Javad and William F. Smith. Foundations of Materials Science and Engineering, 4th edition. McGraw-Hill, 2006. ISBN   0-07-125690-3.
• Hibbeler, R.C. Statics and Mechanics of Materials, SI Edition. Prentice-Hall, 2004. ISBN   0-13-129011-8.
• Lebedev, Leonid P. and Michael J. Cloud. Approximating Perfection: A Mathematician's Journey into the World of Mechanics. Princeton University Press, 2004. ISBN   0-691-11726-8.
• Chapter 10 – Strength of Elastomers, A.N. Gent, W.V. Mars, In: James E. Mark, Burak Erman and Mike Roland, Editor(s), The Science and Technology of Rubber (Fourth Edition), Academic Press, Boston, 2013, Pages 473–516, ISBN   9780123945846, 10.1016/B978-0-12-394584-6.00010-8
• Mott, Robert L. Applied Strength of Materials, 4th edition. Prentice-Hall, 2002. ISBN   0-13-088578-9.
• Popov, Egor P. Engineering Mechanics of Solids. Prentice Hall, Englewood Cliffs, N. J., 1990. ISBN   0-13-279258-3.
• Ramamrutham, S. Strength of Materials.
• Shames, I.H. and F.A. Cozzarelli. Elastic and inelastic stress analysis. Prentice-Hall, 1991. ISBN   1-56032-686-7.
• Timoshenko S. Strength of Materials, 3rd edition. Krieger Publishing Company, 1976, ISBN   0-88275-420-3.
• Timoshenko, S.P. and D.H. Young. Elements of Strength of Materials, 5th edition. (MKS System)
• Davidge, R.W., Mechanical Behavior of Ceramics, Cambridge Solid State Science Series, (1979)
• Lawn, B.R., Fracture of Brittle Solids, Cambridge Solid State Science Series, 2nd Edn. (1993)
• Green, D., An Introduction to the Mechanical Properties of Ceramics, Cambridge Solid State Science Series, Eds. Clarke, D.R., Suresh, S., Ward, I.M.Babu Tom.K (1998)

External links

• Failure theories
• Case studies in structural failure