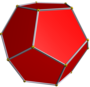
In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.

In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from Latin stella, "star". Stellation is the reciprocal or dual process to faceting.

In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.

In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.

In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.

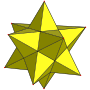
In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.

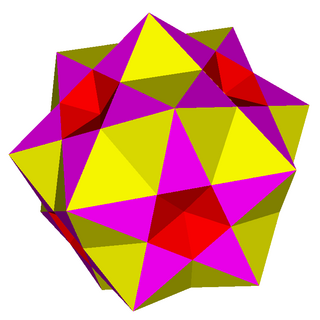
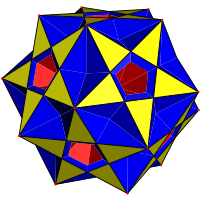
In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a{5,3}, as an altered dodecahedron, and Coxeter diagram or .

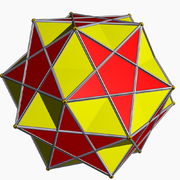
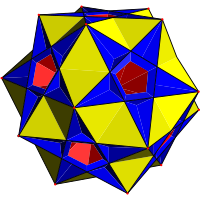
In geometry, the great icosidodecahedron is a nonconvex uniform polyhedron, indexed as U54. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 30 vertices. It is given a Schläfli symbol r{3,5⁄2}. It is the rectification of the great stellated dodecahedron and the great icosahedron. It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

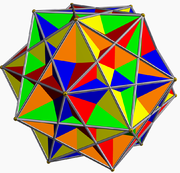
In geometry, the ditrigonal dodecadodecahedron (or ditrigonary dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U41. It has 24 faces (12 pentagons and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol b{5,5⁄2}, as a blended great dodecahedron, and Coxeter diagram . It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 5⁄3 5, and Coxeter diagram .

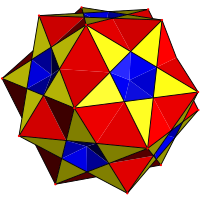
In geometry, the nonconvex great rhombicosidodecahedron is a nonconvex uniform polyhedron, indexed as U67. It has 62 faces (20 triangles, 30 squares and 12 pentagrams), 120 edges, and 60 vertices. It is also called the quasirhombicosidodecahedron. It is given a Schläfli symbol rr{5⁄3,3}. Its vertex figure is a crossed quadrilateral.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.

The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876.

In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both.
In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive.

In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces, 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron.