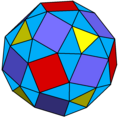
Snub rhombicuboctahedron

Snub rhombicuboctahedron
Schläfli symbol	srr{4,3} = ${\displaystyle sr{\begin{Bmatrix}4\\3\end{Bmatrix}}}$
Conway notation	saC
Faces	74: 8+48 {3} 6+12 {4}
Edges	120
Vertices	48
Symmetry group	O, [4,3]+, (432) order 24
Dual polyhedron	Pentagonal tetracontoctahedron
Properties	convex, chiral

The snub rhombicuboctahedron is a polyhedron, constructed as a truncated rhombicuboctahedron. It has 74 faces: 18 squares, and 56 triangles. It can also be called the Conway snub cuboctahedron in but will be confused with the Coxeter snub cuboctahedron, the snub cube.

Related polyhedra

The snub rhombicuboctahedron can be seen in sequence of operations from the cuboctahedron.

Name	Cubocta- hedron	Truncated cubocta- hedron	Snub cubocta- hedron	Truncated rhombi- cubocta- hedron	Snub rhombi- cubocta- hedron
Coxeter	CO (rC)	tCO (trC)	sCO (srC)	trCO (trrC)	srCO (htrrC)
Conway	aC	taC = bC	sC	taaC = baC	saC
Image
Conway	jC	mC	gC	maC	gaC
Dual

See also

• Expanded cuboctahedron
• Truncated rhombicosidodecahedron

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN   978-1-56881-220-5

External links

• George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input