| Truncated rhombicosidodecahedron | |
|---|---|
 | |
| Schläfli symbol | trr{5,3} = |
| Conway notation | taD = baD |
| Faces | 122: 60 {4} 20 {6} 30 {8} 12 {10} |
| Edges | 360 |
| Vertices | 240 |
| Symmetry group | Ih, [5,3], (*532) order 120 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dual polyhedron | Disdyakis hexecontahedron  |
| Properties | convex |
In geometry, the truncated rhombicosidodecahedron is a polyhedron, constructed as a truncated rhombicosidodecahedron. It has 122 faces: 12 decagons, 30 octagons, 20 hexagons, and 60 squares.
As a zonohedron, it can be constructed with all but 30 octagons as regular polygons. It is 2-uniform, with 2 sets of 120 vertices existing on two distances from its center.
This polyhedron represents the Minkowski sum of a truncated icosidodecahedron, and a rhombic triacontahedron. [1]
The truncated icosidodecahedron is similar, with all regular faces, and 4.6.10 vertex figure. Also see the truncated rhombirhombicosidodecahedron.
| truncated icosidodecahedron | Truncated rhombicosidodecahedron |
|---|---|
 4.6.10 |  4.8.10 and 4.6.8 |
The truncated rhombicosidodecahedron can be seen in sequence of rectification and truncation operations from the icosidodecahedron. A further alternation step leads to the snub rhombicosidodecahedron.
| Name | Icosidodeca- hedron | Rhomb- icosidodeca- hedron | Truncated rhomb- icosidodeca- hedron | Snub rhomb- icosidodeca- hedron |
|---|---|---|---|---|
| Coxeter | ID (rD) | rID (rrD) | trID (trrD) | srID (htrrD) |
| Conway | aD | aaD = eD | taaD = baD | saD |
| Image |  |  |  |  |
| Conway | jD | oD | maD | gaD |
| Dual |  |  |  |  |
In geometry, an icosidodecahedron is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.
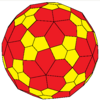
In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
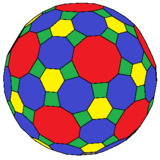
In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.
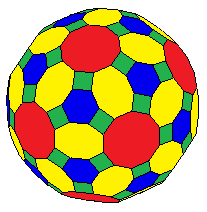
In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.
In geometry, a deltoidal hexecontahedron is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices.
In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.
In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.
In geometry, an alternation or partial truncation, is an operation on a polygon, polyhedron, tiling, or higher dimensional polytope that removes alternate vertices.
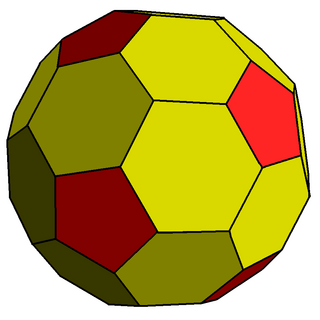
In geometry, the chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.
In geometry, the pentakis icosidodecahedron or subdivided icosahedron is a convex polyhedron with 80 triangular faces, 120 edges, and 42 vertices. It is a dual of the truncated rhombic triacontahedron.
In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces, 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron.
In the geometry of hyperbolic 3-space, the dodecahedral-icosahedral honeycomb is a uniform honeycomb, constructed from dodecahedron, icosahedron, and icosidodecahedron cells, in a rhombicosidodecahedron vertex figure.
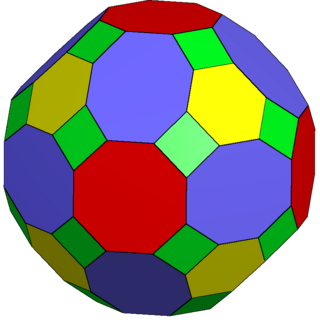
The truncated rhombicuboctahedron is a polyhedron, constructed as a truncation of the rhombicuboctahedron. It has 50 faces consisting of 18 octagons, 8 hexagons, and 24 squares. It can fill space with the truncated cube, truncated tetrahedron and triangular prism as a truncated runcic cubic honeycomb.
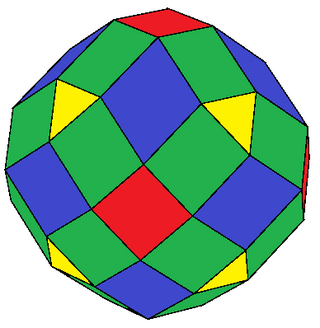
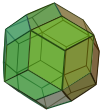
The expanded cuboctahedron is a polyhedron constructed by expansion of the cuboctahedron. It has 50 faces: 8 triangles, 30 squares, and 12 rhombs. The 48 vertices exist at two sets of 24, with a slightly different distance from its center.
The expanded icosidodecahedron is a polyhedron, constructed as an expanded icosidodecahedron. It has 122 faces: 20 triangles, 60 squares, 12 pentagons, and 30 rhombs. The 120 vertices exist at two sets of 60, with a slightly different distance from its center.
In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |
