In geometry, an Archimedean solid is one of the 13 solids first enumerated by Archimedes. They are the convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids and excluding the prisms and antiprisms. They differ from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

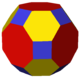
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is the only radially equilateral convex polyhedron.
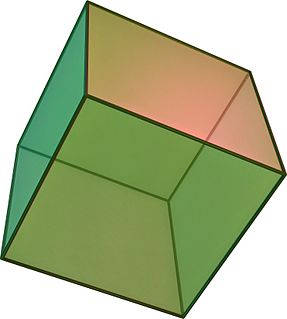
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.

In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides (J1); it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform before they refer to it as a “Johnson solid”.

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each one. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.
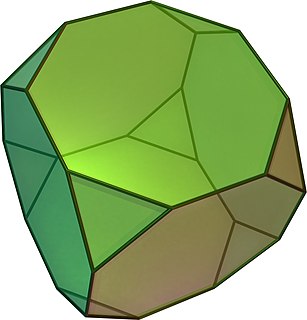
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

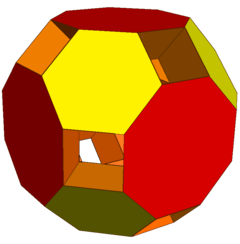
In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In Euclidean geometry, rectification, also known as critical truncation or complete-truncation is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.

In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
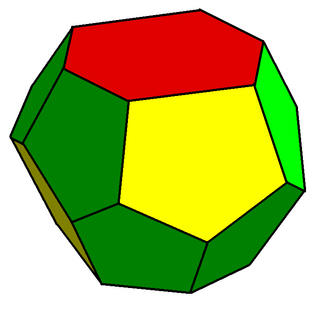
A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.
A pseudo-uniform polyhedron is a polyhedron which has regular polygons as faces and has the same vertex configuration at all vertices but is not vertex-transitive: it is not true that for any two vertices, there exists a symmetry of the polyhedron mapping the first isometrically onto the second. Thus, although all the vertices of a pseudo-uniform polyhedron appear the same, it is not isogonal. They are called pseudo-uniform polyhedra due to their resemblance to some true uniform polyhedra.

In geometry, the crossed square cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex square cupola. It can be obtained as a slice of the nonconvex great rhombicuboctahedron or quasirhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagram.

The expanded cuboctahedron is a polyhedron, constructed as an expanded cuboctahedron. It has 50 faces: 8 triangles, 30 squares, and 12 rhombs. The 48 vertices exist at two sets of 24, with a slightly different distance from its center.

The expanded icosidodecahedron is a polyhedron, constructed as an expanded icosidodecahedron. It has 122 faces: 20 triangles, 60 squares, 12 pentagons, and 30 rhombs. The 120 vertices exist at two sets of 60, with a slightly different distance from its center.

In geometry, chamfering or edge-truncation is a topological operator that modifies one polyhedron into another. It is similar to expansion, moving faces apart and outward, but also maintains the original vertices. For polyhedra, this operation adds a new hexagonal face in place of each original edge.