
In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.
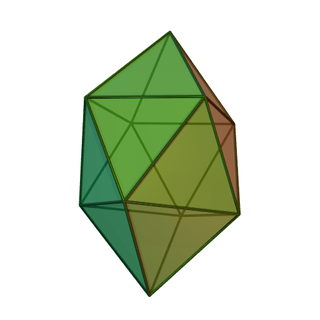
In geometry, the gyroelongated square bipyramid, heccaidecadeltahedron, or tetrakis square antiprism is one of the Johnson solids. As the name suggests, it can be constructed by gyroelongating an octahedron by inserting a square antiprism between its congruent halves. It is one of the eight strictly-convex deltahedra.

In geometry, the elongated square bipyramid is one of the Johnson solids. As the name suggests, it can be constructed by elongating an octahedron by inserting a cube between its congruent halves. It can also be seen as 4 lunes linked together with squares to squares and triangles to triangles.

In geometry, the elongated pentagonal bipyramid or pentakis pentagonal prism is one of the Johnson solids. As the name suggests, it can be constructed by elongating a pentagonal bipyramid by inserting a pentagonal prism between its congruent halves.
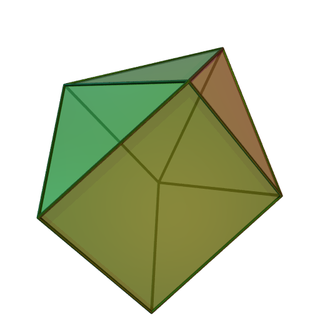
In geometry, the augmented triangular prism is one of the Johnson solids. As the name suggests, it can be constructed by augmenting a triangular prism by attaching a square pyramid to one of its equatorial faces. The resulting solid bears a superficial resemblance to the gyrobifastigium, the difference being that the latter is constructed by attaching a second triangular prism, rather than a square pyramid.
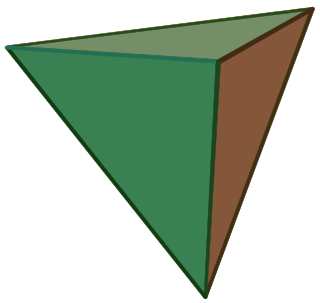
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

In geometry, a decahedron is a polyhedron with ten faces. There are 32300 topologically distinct decahedra, and none are regular, so this name does not identify a specific type of polyhedron except for the number of faces.

In geometry, an n-agonal bifrustum is a polyhedron composed of three parallel planes of n-agons, with the middle plane largest and usually the top and bottom congruent.
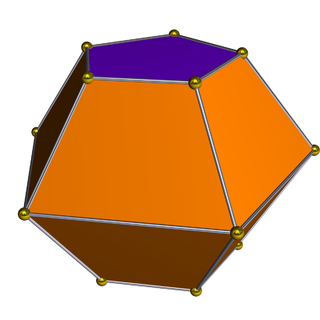
In geometry, the pentagonal bifrustum or truncated pentagonal bipyramid is the third in an infinite series of bifrustum polyhedra. It has 10 trapezoidal and 2 pentagonal faces.

In geometry, the triangular bifrustum is the second in an infinite series of bifrustum polyhedra. It has 6 trapezoid and 2 triangle faces. It may also be called the truncated triangular bipyramid; however, that term is ambiguous, as it may also refer to polyhedra formed by truncating all five vertices of a triangular bipyramid.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.

In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane.

In geometry, a rectified prism is one of an infinite set of polyhedra, constructed as a rectification of an n-gonal prism, truncating the vertices down to the midpoint of the original edges. In Conway polyhedron notation, it is represented as aPn, an ambo-prism. The lateral squares or rectangular faces of the prism become squares or rhombic faces, and new isosceles triangle faces are truncations of the original vertices.



















