In chemistry and crystallography, a symmetry element is a point, line, or plane about which symmetry operations can take place. In particular, a symmetry element can be a mirror plane, an axis of rotation (either proper and improper), or a center of inversion. [1] [2] [3] For an object such as a molecule or a crystal, a symmetry element corresponds to a set of symmetry operations, which are the rigid transformations employing the symmetry element that leave the object unchanged. The set containing these operations form one of the symmetry groups of the object. The elements of this symmetry group should not be confused with the "symmetry element" itself. Loosely, a symmetry element is the geometric set of fixed points of a symmetry operation. For example, for rotation about an axis, the points on the axis do not move and in a reflection the points that remain unchanged make up a plane of symmetry.
The identity symmetry element is found in all objects and is denoted E. [4] It corresponds to an operation of doing nothing to the object. Because every molecule is indistinguishable from itself if nothing is done to it, every object possesses at least the identity element. An object having no symmetry elements other than E is called asymmetric. Such an object is necessarily chiral. [5]
Mirror planes are denoted by σ. In a molecule that also has an axis of symmetry, a mirror plane that includes the axis is called a vertical mirror plane and is labeled σv , while one perpendicular to the axis is called a horizontal mirror plane and is labeled σh . A vertical mirror plane that bisects the angle between two C2 axes is called a dihedral mirror plane, σd . [6]
Rotational symmetry, also known as radial symmetry, is represented by an axis about which the object rotates in its corresponding symmetry operation. A group of proper rotations is denoted as Cn, where the degrees of rotation that restore the object is 360/n (C2= 180º rotation, C3= 120º rotation, C4= 90º rotation, C5= 72º rotation). [4] The Cn notation is also used for the related, more abstract, cyclic group.
An improper rotation is the composition of a rotation about an axis, and reflection in a plane perpendicular to that axis. [2] The order in which the rotation and reflection are performed does not matter (that is, these operations commute). Improper rotation is also defined as the composition of a rotation about an axis, and inversion about a point on the axis. [3] These definitions are equivalent because inversion about a point is equivalent to rotation by 180° about any axis, followed by mirroring about a plane perpendicular to that axis. The symmetry elements for improper rotation are the rotation axis, and either the mirror plane, the inversion point, or both. The improper rotation group of order 2n is denoted S2n.
For inversion, denoted i, there must be a point in the center of an object that is the inversion center. Inversion consists of passing each point through the center of inversion and out to the same distance on the other side of the molecule. In the inversion operation for 3D coordinates, the inversion center is the origin (0,0,0). When an object is inverted, the position vector of a point in an object, ⟨x,y,z⟩, is inverted to ⟨-x,-y,-z⟩.
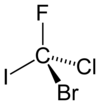
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).
In abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.
In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.
In geometry, an improper rotation is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicular to that axis. Reflection and inversion are each special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation. It is used as a symmetry operation in the context of geometric symmetry, molecular symmetry and crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have improper rotation symmetry.
A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.
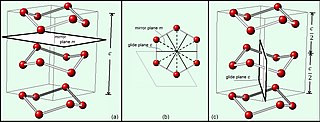
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of the pattern that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.
In crystallography, a crystallographic point group is a set of symmetry operations, corresponding to one of the point groups in three dimensions, such that each operation would leave the structure of a crystal unchanged i.e. the same kinds of atoms would be placed in similar positions as before the transformation. For example, in many crystals in the cubic crystal system, a rotation of the unit cell by 90 degrees around an axis that is perpendicular to one of the faces of the cube is a symmetry operation that moves each atom to the location of another atom of the same kind, leaving the overall structure of the crystal unaffected.
The Schoenfliesnotation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation.
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.
A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dihn.
In three dimensional geometry, there are four infinite series of point groups in three dimensions (n≥1) with n-fold rotational or reflectional symmetry about one axis (by an angle of 360°/n) that does not change the object.
In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.
In group theory, geometry, representation theory and molecular geometry, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, as transformations of an object in space, rotations, reflections and inversions are all symmetry operations. Such symmetry operations are performed with respect to symmetry elements. In the context of molecular symmetry, a symmetry operation is a permutation of atoms such that the molecule or crystal is transformed into a state indistinguishable from the starting state. Two basic facts follow from this definition, which emphasizes its usefulness.
In chemistry, molecular symmetry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain many of a molecule's chemical properties, such as whether or not it has a dipole moment, as well as its allowed spectroscopic transitions. To do this it is necessary to use group theory. This involves classifying the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Symmetry is useful in the study of molecular orbitals, with applications to the Hückel method, to ligand field theory, and to the Woodward-Hoffmann rules. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry discuss symmetry. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materials.
In geometry, a point reflection is a transformation of affine space in which every point is reflected across a specific fixed point. When dealing with crystal structures and in the physical sciences the terms inversion symmetry, inversion center or centrosymmetric are more commonly used.
Molecular symmetry in physics and chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in the application of Quantum Mechanics in physics and chemistry, for example it can be used to predict or explain many of a molecule's properties, such as its dipole moment and its allowed spectroscopic transitions, without doing the exact rigorous calculations. To do this it is necessary to classify the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Among all the molecular symmetries, diatomic molecules show some distinct features and they are relatively easier to analyze.
In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.