Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set A of hyperplanes in a linear, affine, or projective space S. Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice. The intersection semilattice of A, written L(A), is the set of all subspaces that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc. (excluding, in the affine case, the empty set). These intersection subspaces of A are also called the flats ofA. The intersection semilattice L(A) is partially ordered by reverse inclusion.

Frank Harary was an American mathematician, who specialized in graph theory. He was widely recognized as one of the "fathers" of modern graph theory. Harary was a master of clear exposition and, together with his many doctoral students, he standardized the terminology of graphs. He broadened the reach of this field to include physics, psychology, sociology, and even anthropology. Gifted with a keen sense of humor, Harary challenged and entertained audiences at all levels of mathematical sophistication. A particular trick he employed was to turn theorems into games—for instance, students would try to add red edges to a graph on six vertices in order to create a red triangle, while another group of students tried to add edges to create a blue triangle. Because of the theorem on friends and strangers, one team or the other would have to win.
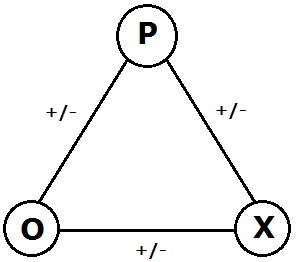
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.

In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices, thus it is "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.
Claudia Zaslavsky was an American mathematics teacher and ethnomathematician.
A gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g (a group element), then in the other direction it has label g −1. The label function φ therefore has the property that it is defined differently, but not independently, on the two different orientations, or directions, of an edge e. The group G is called the gain group, φ is the gain function, and the value φ(e) is the gain of e (in some indicated direction). A gain graph is a generalization of a signed graph, where the gain group G has only two elements. See Zaslavsky (1989, 1991).

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the number of weak orderings on a set of n elements. Starting from n = 0, these numbers are
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution without any fixed points. Skew-symmetric graphs are identical to the double covering graphs of bidirected graphs.
The mathematical field of combinatorics was studied to varying degrees in numerous ancient societies. Its study in Europe dates to the work of Leonardo Fibonacci in the 13th century AD, which introduced Arabian and Indian ideas to the continent. It has continued to be studied in the modern era.

In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of male-female couples at a round dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas and independently, a few years earlier, by Peter Guthrie Tait in connection with knot theory. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is
András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
In geometry, the moment curve is an algebraic curve in d-dimensional Euclidean space given by the set of points with Cartesian coordinates of the form
The FKT algorithm, named after Fisher, Kasteleyn, and Temperley, counts the number of perfect matchings in a planar graph in polynomial time. This same task is #P-complete for general graphs. For matchings that are not required to be perfect, counting them remains #P-complete even for planar graphs. The key idea of the FKT algorithm is to convert the problem into a Pfaffian computation of a skew-symmetric matrix derived from a planar embedding of the graph. The Pfaffian of this matrix is then computed efficiently using standard determinant algorithms.
Curtis Greene is an American mathematician, specializing in algebraic combinatorics. He is the J. McLain King Professor of Mathematics at Haverford College in Pennsylvania.








