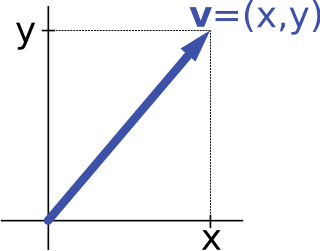In mathematics, a geometric algebra is an extension of elementary algebra to work with geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric product. Multiplication of vectors results in higher-dimensional objects called multivectors. Compared to other formalisms for manipulating geometric objects, geometric algebra is noteworthy for supporting vector division and addition of objects of different dimensions.

In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Euclidean vectors can be added and scaled to form a vector space. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by
Vector calculus or vector analysis is a branch of mathematics concerned with the differentiation and integration of vector fields, primarily in three-dimensional Euclidean space, The term vector calculus is sometimes used as a synonym for the broader subject of multivariable calculus, which spans vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic fields, gravitational fields, and fluid flow.

Josiah Willard Gibbs was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics, explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus and described the Gibbs phenomenon in the theory of Fourier analysis.

In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by H, or in blackboard bold by Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form

Hermann Günther Grassmann was a German polymath known in his day as a linguist and now also as a mathematician. He was also a physicist, general scholar, and publisher. His mathematical work was little noted until he was in his sixties. His work preceded and exceeded the concept which is now known as a vector space. He introduced the Grassmannian, the space which parameterizes all k-dimensional linear subspaces of an n-dimensional vector space V. In linguistics he helped free language history and structure from each other.

In mathematics, the cross product or vector product is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space, and is denoted by the symbol . Given two linearly independent vectors a and b, the cross product, a × b, is a vector that is perpendicular to both a and b, and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product.
The nabla is a triangular symbol resembling an inverted Greek delta: or ∇. The name comes, by reason of the symbol's shape, from the Hellenistic Greek word νάβλα for a Phoenician harp, and was suggested by the encyclopedist William Robertson Smith in an 1870 letter to Peter Guthrie Tait.

In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalars and vectors. Considering a scalar as a degree-zero quantity and a vector as a degree-one quantity, a bivector is of degree two. Bivectors have applications in many areas of mathematics and physics. They are related to complex numbers in two dimensions and to both pseudovectors and vector quaternions in three dimensions. They can be used to generate rotations in a space of any number of dimensions, and are a useful tool for classifying such rotations. They are also used in physics.
In abstract algebra, the algebra of hyperbolic quaternions is a nonassociative algebra over the real numbers with elements of the form
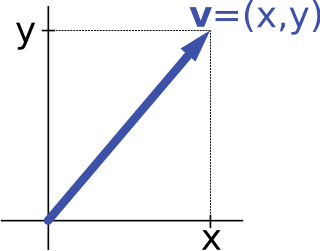
In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more generally, members of a vector space.
In mathematical physics, spacetime algebra (STA) is the application of Clifford algebra Cl1,3(R), or equivalently the geometric algebra G(M4) to physics. Spacetime algebra provides a "unified, coordinate-free formulation for all of relativistic physics, including the Dirac equation, Maxwell equation and General Relativity" and "reduces the mathematical divide between classical, quantum and relativistic physics."
Edwin Bidwell Wilson was an American mathematician, statistician, physicist and general polymath. He was the sole protégé of Yale University physicist Josiah Willard Gibbs and was mentor to MIT economist Paul Samuelson. Wilson had a distinguished academic career at Yale and MIT, followed by a long and distinguished period of service as a civilian employee of the US Navy in the Office of Naval Research. In his latter role, he was awarded the Distinguished Civilian Service Award, the highest honorary award available to a civilian employee of the US Navy. Wilson made broad contributions to mathematics, statistics and aeronautics, and is well-known for producing a number of widely used textbooks. He is perhaps best known for his derivation of the eponymously named Wilson score interval, which is a confidence interval used widely in statistics.

In mathematics, quaternions are a non-commutative number system that extends the complex numbers. Quaternions and their applications to rotations were first described in print by Olinde Rodrigues in all but name in 1840, but independently discovered by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. They find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations.

A History of Vector Analysis (1967) is a book on the history of vector analysis by Michael J. Crowe, originally published by the University of Notre Dame Press. As a scholarly treatment of a reformation in technical communication, the text is a contribution to the history of science. In 2002, Crowe gave a talk summarizing the book, including an entertaining introduction in which he covered its publication history and related the award of a Jean Scott prize of $4000. Crowe had entered the book in a competition for "a study on the history of complex and hypercomplex numbers" twenty-five years after his book was first published.
The Quaternion Society was a scientific society, self-described as an "International Association for Promoting the Study of Quaternions and Allied Systems of Mathematics". At its peak it consisted of about 60 mathematicians spread throughout the academic world that were experimenting with quaternions and other hypercomplex number systems. The group's guiding light was Alexander Macfarlane who served as its secretary initially, and became president in 1909. The association published a Bibliography in 1904 and a Bulletin from 1900 to 1913.
Six-dimensional space is any space that has six dimensions, six degrees of freedom, and that needs six pieces of data, or coordinates, to specify a location in this space. There are an infinite number of these, but those of most interest are simpler ones that model some aspect of the environment. Of particular interest is six-dimensional Euclidean space, in which 6-polytopes and the 5-sphere are constructed. Six-dimensional elliptical space and hyperbolic spaces are also studied, with constant positive and negative curvature.
The following are important identities in vector algebra. Identities that involve the magnitude of a vector , or the dot product of two vectors A·B, apply to vectors in any dimension. Identities that use the cross product A×B are defined only in three dimensions. Most of these relations can be dated to founder of vector calculus Josiah Willard Gibbs, if not earlier.

Elements of Dynamic is a book published by William Kingdon Clifford in 1878. In 1887 it was supplemented by a fourth part and an appendix. The subtitle is "An introduction to motion and rest in solid and fluid bodies". It was reviewed positively, has remained a standard reference since its appearance, and is now available online as a Historical Math Monograph from Cornell University.
In mathematics, a bivector is the vector part of a biquaternion. For biquaternion q = w + xi + yj + zk, w is called the biscalar and xi + yj + zk is its bivector part. The coordinates w, x, y, z are complex numbers with imaginary unit h: