Vibration fatigue

Last updated
Researchers using a machine known as a "shaker" to study the effects of multi-axial vibrations, 2019 Army Research Laboratory multiaxial vibration experiment.jpg
Researchers using a machine known as a "shaker" to study the effects of multi-axial vibrations, 2019

Vibration fatigue is a mechanical engineering term describing material fatigue, caused by forced vibration of random nature. An excited structure responds according to its natural-dynamics modes, which results in a dynamic stress load in the material points. [1] The process of material fatigue is thus governed largely by the shape of the excitation profile and the response it produces. As the profiles of excitation and response are preferably analyzed in the frequency domain it is practical to use fatigue life evaluation methods, that can operate on the data in frequency-domain, s power spectral density (PSD).

Contents

A crucial part of a vibration fatigue analysis is the modal analysis, that exposes the natural modes and frequencies of the vibrating structure and enables accurate prediction of the local stress responses for the given excitation. Only then, when the stress responses are known, can vibration fatigue be successfully characterized.

The more classical approach of fatigue evaluation consists of cycle counting, using the rainflow algorithm and summation by means of the Palmgren-Miner linear damage hypothesis, that appropriately sums the damages of respective cycles. When the time history is not known, because the load is random (e.g. a car on a rough road or a wind driven turbine), those cycles can not be counted. Multiple time histories can be simulated for a given random process, but such procedure is cumbersome and computationally expensive. [2]

Vibration-fatigue methods offer a more effective approach, which estimates fatigue life based on moments of the PSD. This way, a value is estimated, that would otherwise be calculated with the time-domain approach. When dealing with many material nodes, experiencing different responses (e.g. a model in a FEM package), time-histories need not be simulated. It then becomes viable, with the use of vibration-fatigue methods, to calculate fatigue life in many points on the structure and successfully predict where the failure will most probably occur.

Vibration-fatigue-life estimation

Random load description

In a random process, the amplitude can not be described as a function of time, because of its probabilistic nature. However, certain statistical properties can be extracted from a signal sample, representing a realization of a random process, provided the latter is ergodic. An important characteristics for the field of vibration fatigue is the amplitude probability density function, that describes the statistical distribution of peak amplitudes. Ideally, the probability of cycle amplitudes, describing the load severity, could then be deduced directly. However, as this is not always possible, the sought-after probability is often estimated empirically.

Effects of structural dynamics

First natural mode of a cantilever beam. First mode of cantilever animation.gif
First natural mode of a cantilever beam.

Random excitation of the structure produces different responses, depending on the natural dynamics of the structure in question. Different natural modes get excited and each greatly affects the stress distribution in material. The standard procedure is to calculate frequency response functions for the analyzed structure and then obtain the stress responses, based on given loading or excitation. [3] By exciting different modes, the spread of vibration energy over a frequency range directly affects the durability of the structure. Thus the structural dynamics analysis is a key part of vibration-fatigue evaluation.

Vibration-fatigue methods

Calculation of damage intensity is straightforward once the cycle amplitude distribution is known. This distribution can be obtained from a time-history simply by counting cycles. To obtain it from the PSD another approach must be taken.

Various vibration-fatigue methods estimate damage intensity based on moments of the PSD, which characterize the statistical properties of the random process. The formulas for calculating such estimate are empirical (with very few exceptions) and are based on numerous simulations of random processes with known PSD. As a consequence, the accuracy of those methods varies, depending on analyzed response spectra, material parameters and the method itself - some are more accurate than others. [4]

The most commonly used method is the one developed by T. Dirlik in 1985. [5] Recent research on frequency-domain methods of fatigue-life estimation [4] compared well established methods and also recent ones; conclusion showed that the methods by Zhao and Baker, developed in 1992 [6] and by Benasciutti and Tovo, developed in 2004 [7] are also very suitable for vibration-fatigue analysis. For narrow-band approximation of random process analytical expression for damage intensity is given by Miles. [8] There are some approaches with adaptation of narrow-band approximation; Wirsching and Light proposed the empirical correction factor in 1980 [9] and Benasciutti presented α0.75 in 2004. [10] In 2008, Gao and Moan published a spectral method that combines three narrow-band processes. [11] Implementation of those method is given in the Python open-source FLife [12] package.

Applications

Vibration fatigue methods find use wherever the structure experiences loading, that is caused by a random process. These can be the forces that bumps on the road extort on the car chassis, the wind blowing on the wind turbine, waves hitting an offshore construction or a marine vessel. Such loads are first characterized statistically, by measurement and analysis. The data is then used in the product design process. [13]

The computational effectiveness of vibration-fatigue methods in contrast to the classical approach, enables their use in combination with FEM software packages, to evaluate fatigue after the loading is known and the dynamic analysis has been performed. Use of the vibration-fatigue methods is well-suited, as structural analysis is studied in the frequency-domain.

Common practice in the automotive industry is the use of accelerated vibration tests. During the test, a part or a product is exposed to vibration, that are in correlation with those expected during the service-life of the product. To shorten the testing time, the amplitudes are amplified. The excitation spectra used are broad-band and can be evaluated most effectively using vibration-fatigue methods.

See also

Related Research Articles

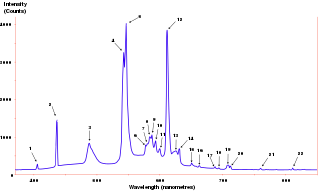
Spectral density Relative importance of certain frequencies in a composite signal

The power spectrum of a time series describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of a certain signal or sort of signal as analyzed in terms of its frequency content, is called its spectrum.

Fatigue (material) Initiation and propagation of cracks in a material due to cyclic loading

In materials science, fatigue is the initiation and propagation of cracks in a material due to cyclic loading. Once a fatigue crack has initiated, it grows a small amount with each loading cycle, typically producing striations on some parts of the fracture surface. The crack will continue to grow until it reaches a critical size, which occurs when the stress intensity factor of the crack exceeds the fracture toughness of the material, producing rapid propagation and typically complete fracture of the structure.

Modal testing

Modal testing is the form of vibration testing of an object whereby the natural (modal) frequencies, modal masses, modal damping ratios and mode shapes of the object under test are determined.

Seismic analysis

Seismic analysis is a subset of structural analysis and is the calculation of the response of a building structure to earthquakes. It is part of the process of structural design, earthquake engineering or structural assessment and retrofit in regions where earthquakes are prevalent.

Structural health monitoring (SHM) involves the observation and analysis of a system over time using periodically sampled response measurements to monitor changes to the material and geometric properties of engineering structures such as bridges and buildings.

A structural load or structural action is a force, deformation, or acceleration applied to structural elements. A load causes stress, deformation, and displacement in a structure. Structural analysis, a discipline in engineering, analyzes the effects of loads on structures and structural elements. Excess load may cause structural failure, so this should be considered and controlled during the design of a structure. Particular mechanical structures—such as aircraft, satellites, rockets, space stations, ships, and submarines—are subject to their own particular structural loads and actions. Engineers often evaluate structural loads based upon published regulations, contracts, or specifications. Accepted technical standards are used for acceptance testing and inspection.

This is an alphabetical list of articles pertaining specifically to structural engineering. For a broad overview of engineering, please see List of engineering topics. For biographies please see List of engineers.

Structural dynamics is a type of structural analysis which covers the behavior of a structure subjected to dynamic loading. Dynamic loads include people, wind, waves, traffic, earthquakes, and blasts. Any structure can be subjected to dynamic loading. Dynamic analysis can be used to find dynamic displacements, time history, and modal analysis.

Modal analysis

Modal analysis is the study of the dynamic properties of systems in the frequency domain. Examples would include measuring the vibration of a car's body when it is attached to a shaker, or the noise pattern in a room when excited by a loudspeaker.

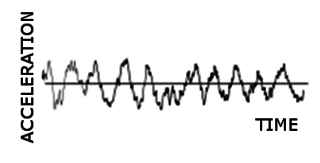
Random vibration

In mechanical engineering, random vibration is motion which is non-deterministic, meaning that future behavior cannot be precisely predicted. The randomness is a characteristic of the excitation or input, not the mode shapes or natural frequencies. Some common examples include an automobile riding on a rough road, wave height on the water, or the load induced on an airplane wing during flight. Structural response to random vibration is usually treated using statistical or probabilistic approaches. Mathematically, random vibration is characterized as an ergodic and stationary process.

The Extreme Response Spectrum (ERS) is defined as a curve giving the value of the highest peak of the response of a linear Single Degree of Freedom System to vibration, according to its natural frequency, for a given damping ratio. The response is described here by the relative movement of the mass of this system in relation to its support. The x-axis refers to the natural frequency and the y-axis to the highest peak multiplied by the square of the quantity, by analogy with the relative displacement shock response spectrum.

In geophysics, geology, civil engineering, and related disciplines, seismic noise is a generic name for a relatively persistent vibration of the ground, due to a multitude of causes, that is often a non-interpretable or unwanted component of signals recorded by seismometers.

Vibratory Stress Relief, often abbreviated VSR, is a non-thermal stress relief method used by the metal working industry to enhance the dimensional stability and mechanical integrity of castings, forgings, and welded components, chiefly for two categories of these metal workpieces:

Ambient modal identification, also known as operational modal analysis (OMA), aims at identifying the modal properties of a structure based on vibration data collected when the structure is under its operating conditions, i.e., no initial excitation or known artificial excitation. The modal properties of a structure include primarily the natural frequencies, damping ratios and mode shapes. In an ambient vibration test the subject structure can be under a variety of excitation sources which are not measured but are assumed to be 'broadband random'. The latter is a notion that one needs to apply when developing an ambient identification method. The specific assumptions vary from one method to another. Regardless of the method used, however, proper modal identification requires that the spectral characteristics of the measured response reflect the properties of the modes rather than those of the excitation.

Bayesian operational modal analysis (BAYOMA) adopts a Bayesian system identification approach for operational modal analysis (OMA). Operational modal analysis aims at identifying the modal properties of a constructed structure using only its (output) vibration response measured under operating conditions. The (input) excitations to the structure are not measured but are assumed to be 'ambient'. In a Bayesian context, the set of modal parameters are viewed as uncertain parameters or random variables whose probability distribution is updated from the prior distribution to the posterior distribution. The peak(s) of the posterior distribution represents the most probable value(s) (MPV) suggested by the data, while the spread of the distribution around the MPV reflects the remaining uncertainty of the parameters.

Low cycle fatigue has two fundamental characteristics: plastic deformation in each cycle; and low cycle phenomenon, in which the materials have finite endurance for this type of load. The term cycle refers to repeated applications of stress that lead to eventual fatigue and failure; low-cycle pertains to a long period between applications.

Solder fatigue is the mechanical degradation of solder due to deformation under cyclic loading. This can often occur at stress levels below the yield stress of solder as a result of repeated temperature fluctuations, mechanical vibrations, or mechanical loads. Techniques to evaluate solder fatigue behavior include finite element analysis and semi-analytical closed-form equations.

Fatigue of welded joints can occur when poorly made or highly stressed welded joints are subjected to cyclic loading. Welding is a manufacturing method used to join various materials in order to form an assembly. During welding, joints are formed between two or more separate pieces of material which can introduce defects or residual stresses. Under cyclic loading these defects can grow a fatigue crack, causing the assembly to fail even if these cyclic stresses are low and smaller than the base material and weld filler material yield stress. Hence, the fatigue strength of a welded joint does not correlate to the fatigue strength of the base material. Incorporating design considerations in the development phase can reduce failures due to fatigue in welded joints.

Fatigue testing Determination of a material or structures resiliency against cyclic loading

Fatigue testing is a specialised form of mechanical testing that is performed by applying cyclic loading to a coupon or structure. These tests are used either to generate fatigue life and crack growth data, identify critical locations or demonstrate the safety of a structure that may be susceptible to fatigue. Fatigue tests are used on a range of components from coupons through to full size test articles such as automobiles and aircraft.

Fastran is a computer program for calculating the rate of fatigue crack growth by combining crack growth equations and a simulation of the plasticity at the crack tip.

References

  1. ↑ Nuno Manuel Mendes, Maia (1998). Theoretical and experimental modal analysis (Reprinted. ed.). Baldock: Research Studies Press. ISBN   0863802087.
  2. ↑ Sarkani, Loren D. Lutes, Shahram (2004). Random vibrations analysis of structural and mechanical systems ([Online-Ausg.] ed.). Amsterdam: Elsevier. ISBN   9780750677653.
  3. ↑ Slavič, Janko; Boltežar, Miha; Mršnik, Matjaž; Česnik, Martin; Javh, Jaka (2020). Vibration Fatigue by Spectral Methods: From Structural Dynamics to Fatigue Damage – Theory and Experiments (1st ed.). Amsterdam, Netherlands: Elsevier. doi:10.1016/C2019-0-04580-3. ISBN   9780128221907. S2CID   243156155.
  4. 1 2 Mršnik, Matjaž; Slavič, Janko; Boltežar, Miha (31 July 2012). "Frequency-domain methods for a vibration-fatigue-life estimation - application to real data". International Journal of Fatigue. 47: 8–17. doi:10.1016/j.ijfatigue.2012.07.005.
  5. ↑ Dirlik, Turan (1985). Application of computers in fatigue analysis (Ph.D.). University of Warwick.
  6. ↑ Zhao, W; Baker, M (1 March 1992). "On the probability density function of rainflow stress range for stationary Gaussian processes". International Journal of Fatigue. 14 (2): 121–135. doi:10.1016/0142-1123(92)90088-T.
  7. ↑ Benasciutti, D; Tovo, R (1 August 2005). "Spectral methods for lifetime prediction under wide-band stationary random processes". International Journal of Fatigue. 27 (8): 867–877. doi:10.1016/j.ijfatigue.2004.10.007.
  8. ↑ Miles, John W. (1954). "On structural fatigue under random loading". Journal of the Aeronautical Sciences. 21 (11): 753–762. doi:10.2514/8.3199.
  9. ↑ Wirsching, Paul H.; Light, Mark C. (1980). "Fatigue under wide band random stresses". Journal of the Structural Division. 106 (7): 1593–1607. doi:10.1061/JSDEAG.0005477.
  10. ↑ Benasciutti, Denis; Tovo, Roberto (2004). Rainflow cycle distribution and fatigue damage in Gaussian random loadings (Report). Department of Engineering, University of Ferrara.
  11. ↑ Gao, Zhen; Moan, Torgeir (2008). "Frequency-domain fatigue analysis of wide-band stationary Gaussian processes using a trimodal spectral formulation". International Journal of Fatigue. 30 (10–11): 1944–1955. doi:10.1016/j.ijfatigue.2008.01.008.
  12. ↑ "FLife". GitHub . Retrieved 30 September 2020.
  13. ↑ Varoto, Kenneth G. McConnell, Paulo S. (2008). Vibration testing : theory and practice (2nd ed.). Hoboken, N.J.: John Wiley & Sons. ISBN   978-0-471-66651-6.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.