Order of magnitude

Last updated February 15, 2024

An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic distributions are common in nature and considering the order of magnitude of values sampled from such a distribution can be more intuitive. When the reference value is 10, the order of magnitude can be understood as the number of digits in the base-10 representation of the value. Similarly, if the reference value is one of some powers of 2, since computers store data in a binary format, the magnitude can be understood in terms of the amount of computer memory needed to store that value.

Definition

Generally, the order of magnitude of a number is the smallest power of 10 used to represent that number.^[2] To work out the order of magnitude of a number $N$ , the number is first expressed in the following form:

N=a\times 10^{b}

where ${\frac {1}{\sqrt {10}}}\leq a<{\sqrt {10}}$ , or approximately $0.316\lesssim a\lesssim 3.16$ . Then, $b$ represents the order of magnitude of the number. The order of magnitude can be any integer. The table below enumerates the order of magnitude of some numbers in light of this definition:

Number $N$	Expression in $N=a\times 10^{b}$	Order of magnitude $b$
0.2	2 × 10⁻¹	−1
1	1 × 10⁰	0
5	0.5 × 10¹	1
6	0.6 × 10¹	1
31	3.1 × 10¹	1
32	0.32 × 10²	2
999	0.999 × 10³	3
1000	1 × 10³	3

The geometric mean of $10^{b-1/2}$ and $10^{b+1/2}$ is $10^{b}$ , meaning that a value of exactly $10^{b}$ (i.e., $a=1$ ) represents a geometric halfway point within the range of possible values of $a$ .

Some use a simpler definition where $0.5\leq a<5$ ,^[3] perhaps because the arithmetic mean of $10^{b}$ and $10^{b+c}$ approaches $5\times 10^{b+c-1}$ for increasing $c$ .^{[ citation needed ]} This definition has the effect of lowering the values of $b$ slightly:

Number $N$	Expression in $N=a\times 10^{b}$	Order of magnitude $b$
0.2	2 × 10⁻¹	−1
1	1 × 10⁰	0
5	0.5 × 10¹	1
6	0.6 × 10¹	1
31	3.1 × 10¹	1
32	3.2 × 10¹	1
999	0.999 × 10³	3
1000	1 × 10³	3

Uses

Orders of magnitude are used to make approximate comparisons. If numbers differ by one order of magnitude, x is about ten times different in quantity than y. If values differ by two orders of magnitude, they differ by a factor of about 100. Two numbers of the same order of magnitude have roughly the same scale: the larger value is less than ten times the smaller value. The growing amounts of Internet data have led to addition of new SI prefixes over time, most recently in 2022.^[4]

In words	Prefix (Symbol)	Decimal	Power of ten	Order of magnitude
nonillionth	quecto- (q)	0.000000000000000000000000000001	10⁻³⁰	−30
octillionth	ronto- (r)	0.000000000000000000000000001	10⁻²⁷	−27
septillionth	yocto- (y)	0.000000000000000000000001	10⁻²⁴	−24
sextillionth	zepto- (z)	0.000000000000000000001	10⁻²¹	−21
quintillionth	atto- (a)	0.000000000000000001	10⁻¹⁸	−18
quadrillionth	femto- (f)	0.000000000000001	10⁻¹⁵	−15
trillionth	pico- (p)	0.000000000001	10⁻¹²	−12
billionth	nano- (n)	0.000000001	10⁻⁹	−9
millionth	micro- (µ)	0.000001	10⁻⁶	−6
thousandth	milli- (m)	0.001	10⁻³	−3
hundredth	centi- (c)	0.01	10⁻²	−2
tenth	deci- (d)	0.1	10⁻¹	−1
one		1	10⁰	0
ten	deca- (da)	10	10¹	1
hundred	hecto- (h)	100	10²	2
thousand	kilo- (k)	1000	10³	3
million	mega- (M)	1000000	10⁶	6
billion	giga- (G)	1000000000	10⁹	9
trillion	tera- (T)	1000000000000	10¹²	12
quadrillion	peta- (P)	1000000000000000	10¹⁵	15
quintillion	exa- (E)	1000000000000000000	10¹⁸	18
sextillion	zetta- (Z)	1000000000000000000000	10²¹	21
septillion	yotta- (Y)	1000000000000000000000000	10²⁴	24
octillion	ronna- (R)	1000000000000000000000000000	10²⁷	27
nonillion	quetta- (Q)	1000000000000000000000000000000	10³⁰	30
In words	Prefix (Symbol)	Decimal	Power of ten	Order of magnitude

Calculating the order of magnitude

The order of magnitude of a number is, intuitively speaking, the number of powers of 10 contained in the number. More precisely, the order of magnitude of a number can be defined in terms of the common logarithm, usually as the integer part of the logarithm, obtained by truncation.^{[ contradictory ]} For example, the number 4000000 has a logarithm (in base 10) of 6.602; its order of magnitude is 6. When truncating, a number of this order of magnitude is between 10⁶ and 10⁷. In a similar example, with the phrase "seven-figure income", the order of magnitude is the number of figures minus one, so it is very easily determined without a calculator to be 6. An order of magnitude is an approximate position on a logarithmic scale.

Order-of-magnitude estimate

An order-of-magnitude estimate of a variable, whose precise value is unknown, is an estimate rounded to the nearest power of ten. For example, an order-of-magnitude estimate for a variable between about 3 billion and 30 billion (such as the human population of the Earth) is 10 billion. To round a number to its nearest order of magnitude, one rounds its logarithm to the nearest integer. Thus 4000000, which has a logarithm (in base 10) of 6.602, has 7 as its nearest order of magnitude, because "nearest" implies rounding rather than truncation. For a number written in scientific notation, this logarithmic rounding scale requires rounding up to the next power of ten when the multiplier is greater than the square root of ten (about 3.162). For example, the nearest order of magnitude for 1.7×10⁸ is 8, whereas the nearest order of magnitude for 3.7×10⁸ is 9. An order-of-magnitude estimate is sometimes also called a zeroth order approximation.

Order of magnitude difference

An order-of-magnitude difference between two values is a factor of 10. For example, the mass of the planet Saturn is 95 times that of Earth, so Saturn is two orders of magnitude more massive than Earth. Order-of-magnitude differences are called decades when measured on a logarithmic scale.

Non-decimal orders of magnitude

Other orders of magnitude may be calculated using bases other than 10. The ancient Greeks ranked the nighttime brightness of celestial bodies by 6 levels in which each level was the fifth root of one hundred (about 2.512) as bright as the nearest weaker level of brightness,^{[ citation needed ]} and thus the brightest level being 5 orders of magnitude brighter than the weakest indicates that it is (100^1/5)⁵ or a factor of 100 times brighter. The modernized version has however turned into a logarithmic scale with non-integer values.

The different decimal numeral systems of the world use a larger base to better envision the size of the number, and have created names for the powers of this larger base. The table shows what number the order of magnitude aim at for base 10 and for base 1000000. It can be seen that the order of magnitude is included in the number name in this example, because bi- means 2 and tri- means 3 (these make sense in the long scale only), and the suffix -illion tells that the base is 1000000. But the number names billion, trillion themselves (here with other meaning than in the first chapter) are not names of the orders of magnitudes, they are names of "magnitudes", that is the numbers1000000000000 etc.

Order of magnitude	Is log₁₀ of	Is log_1000000 of	Short scale	Long scale
1	10	1000000	million	million
2	100	1000000000000	trillion	billion
3	1000	1000000000000000000	quintillion	trillion

SI units in the table at right are used together with SI prefixes, which were devised with mainly base 1000 magnitudes in mind. The IEC standard prefixes with base 1024 were invented for use in electronic technology.

Extremely large numbers

For extremely large numbers, a generalized order of magnitude can be based on their double logarithm or super-logarithm. Rounding these downward to an integer gives categories between very "round numbers", rounding them to the nearest integer and applying the inverse function gives the "nearest" round number.

The double logarithm yields the categories:

..., 1.0023–1.023, 1.023–1.26, 1.26–10, 10–10¹⁰, 10¹⁰–10¹⁰⁰, 10¹⁰⁰–10¹⁰⁰⁰, ...

(the first two mentioned, and the extension to the left, may not be very useful, they merely demonstrate how the sequence mathematically continues to the left).

The super-logarithm yields the categories:

0–1, 1–10, 10–10¹⁰, 10¹⁰–10^10¹⁰, 10^10¹⁰–10^{10^10¹⁰}, ... or

0–⁰10, ⁰10–¹10, ¹10–²10, ²10–³10, ³10–⁴10, ...

The "midpoints" which determine which round number is nearer are in the first case:

1.076, 2.071, 1453, 4.20×10³¹, 1.69×10³¹⁶,...

and, depending on the interpolation method, in the second case

−0.301, 0.5, 3.162, 1453, 1×10¹⁴⁵³,

(10\uparrow )^{1}10^{1453}

,

(10\uparrow )^{2}10^{1453}

,... (see notation of extremely large numbers)

For extremely small numbers (in the sense of close to zero) neither method is suitable directly, but the generalized order of magnitude of the reciprocal can be considered.

Similar to the logarithmic scale one can have a double logarithmic scale (example provided here) and super-logarithmic scale. The intervals above all have the same length on them, with the "midpoints" actually midway. More generally, a point midway between two points corresponds to the generalised f-mean with f(x) the corresponding function log log x or slog x. In the case of log log x, this mean of two numbers (e.g. 2 and 16 giving 4) does not depend on the base of the logarithm, just like in the case of log x (geometric mean, 2 and 8 giving 4), but unlike in the case of log log log x (4 and 65536 giving 16 if the base is 2, but not otherwise).

Related Research Articles

In mathematics, the logarithm is the inverse function to exponentiation. That means that the logarithm of a number $x$ to the base $b$ is the exponent to which $b$ must be raised to produce $x$ . For example, since $1000 = 10 3$ , the logarithm base 10 of $1000$ is $3$ , or $log 10 (1000) = 3$ . The logarithm of $x$ to base $b$ is denoted as $log b (x)$ , or without parentheses, $log b x$ , or even without the explicit base, $log x$ , when no confusion is possible, or when the base does not matter such as in big O notation.

A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.

The natural logarithm of a number is its logarithm to the base of the mathematical constant $e$ , which is an irrational and transcendental number approximately equal to $2.718 281828459$ . The natural logarithm of $x$ is generally written as $ln x$ , $log e x$ , or sometimes, if the base $e$ is implicit, simply $log x$ . Parentheses are sometimes added for clarity, giving $ln(x)$ , $log e (x)$ , or $log(x)$ . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

Benford's law, also known as the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation that in many real-life sets of numerical data, the leading digit is likely to be small. In sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time. Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.

<span class="mw-page-title-main">Exponentiation</span> Arithmetic operation

In mathematics, exponentiation is an operation involving two numbers: the base and the exponent or power. Exponentiation is written as $b n$ , where $b$ is the base and $n$ is the power; this is pronounced as " $b$ (raised) to the $n$ ". When $n$ is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, $b n$ is the product of multiplying $n$ bases:

A logarithmic scale is a way of displaying numerical data over a very wide range of values in a compact way. As opposed to a linear number line in which every unit of distance corresponds to adding by the same amount, on a logarithmic scale, every unit of length corresponds to multiplying the previous value by the same amount. Hence, such a scale is nonlinear. In nonlinear scale, the numbers 1, 2, 3, 4, 5, and so on would not be equally spaced. Rather, the numbers 10, 100, 1000, 10000, and 100000 would be equally spaced. Likewise, the numbers 2, 4, 8, 16, 32, and so on, would be equally spaced. Often exponential growth curves are displayed on a log scale, otherwise they would increase too quickly to fit within a small graph.

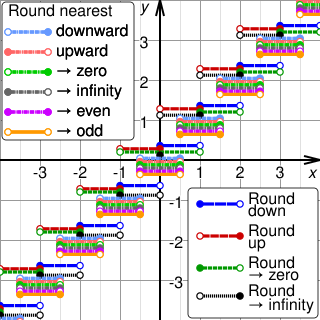
Rounding means replacing a number with an approximate value that has a shorter, simpler, or more explicit representation. For example, replacing $23.4476 with $23.45, the fraction 312/937 with 1/3, or the expression √2 with 1.414.

In mathematics, the common logarithm is the logarithm with base 10. It is also known as the decadic logarithm and as the decimal logarithm, named after its base, or Briggsian logarithm, after Henry Briggs, an English mathematician who pioneered its use, as well as standard logarithm. Historically, it was known as logarithmus decimalis or logarithmus decadis. It is indicated by $log(x)$ , $log 10 (x)$ , or sometimes $Log(x)$ with a capital $L$ ; on calculators, it is printed as "log", but mathematicians usually mean natural logarithm (logarithm with base e ≈ 2.71828) rather than common logarithm when writing "log". To mitigate this ambiguity, the ISO 80000 specification recommends that $log 10 (x)$ should be written $lg(x)$ , and $log e (x)$ should be $ln(x)$ .

Large numbers are numbers significantly larger than those typically used in everyday life, appearing frequently in fields such as mathematics, cosmology, cryptography, and statistical mechanics. They are typically large positive integers, or more generally, large positive real numbers, but may also be other numbers in other contexts. Googology is the study of nomenclature and properties of large numbers.

In mathematics, the binary logarithm is the power to which the number $2$ must be raised to obtain the value $n$ . That is, for any real number $x$ ,

In mathematics, an identity is an equality relating one mathematical expression A to another mathematical expression B, such that A and B produce the same value for all values of the variables within a certain range of validity. In other words, A = B is an identity if A and B define the same functions, and an identity is an equality between functions that are differently defined. For example, $and are identities. Identities are sometimes indicated by the triple bar symbol \equiv instead of =, the equals sign. Formally, an identity is a universally quantified equality.$

In computing, fixed-point is a method of representing fractional (non-integer) numbers by storing a fixed number of digits of their fractional part. Dollar amounts, for example, are often stored with exactly two fractional digits, representing the cents. More generally, the term may refer to representing fractional values as integer multiples of some fixed small unit, e.g. a fractional amount of hours as an integer multiple of ten-minute intervals. Fixed-point number representation is often contrasted to the more complicated and computationally demanding floating-point representation.

In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formula

<span class="mw-page-title-main">Tetration</span> Arithmetic operation

In mathematics, tetration is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though $and the left-exponent x b are common.$

Mental calculation consists of arithmetical calculations using only the human brain, with no help from any supplies or devices such as a calculator. People may use mental calculation when computing tools are not available, when it is faster than other means of calculation, or even in a competitive context. Mental calculation often involves the use of specific techniques devised for specific types of problems. People with unusually high ability to perform mental calculations are called mental calculators or lightning calculators.

One decade is a unit for measuring ratios on a logarithmic scale, with one decade corresponding to a ratio of 10 between two numbers.

<span class="mw-page-title-main">Semi-log plot</span> Type of graph

In science and engineering, a semi-log plot/graph or semi-logarithmicplot/graph has one axis on a logarithmic scale, the other on a linear scale. It is useful for data with exponential relationships, where one variable covers a large range of values, or to zoom in and visualize that - what seems to be a straight line in the beginning - is in fact the slow start of a logarithmic curve that is about to spike and changes are much bigger than thought initially.

A double exponential function is a constant raised to the power of an exponential function. The general formula is $(where a >1 and b >1), which grows much more quickly than an exponential function. For example, if a = b = 10:$

In mathematics, the super-logarithm is one of the two inverse functions of tetration. Just as exponentiation has two inverse functions, roots and logarithms, tetration has two inverse functions, super-roots and super-logarithms. There are several ways of interpreting super-logarithms:

In mathematics, the set of positive real numbers, $is the subset of those real numbers that are greater than zero. The non-negative real numbers, also include zero. Although the symbols and are ambiguously used for either of these, the notation or for and or for has also been widely employed, is aligned with the practice in algebra of denoting the exclusion of the zero element with a star, and should be understandable to most practicing mathematicians.$

References

↑ Brians, Paus. "Orders of Magnitude" . Retrieved 9 May 2013.
↑ "Order of Magnitude". Wolfram MathWorld. Retrieved 3 January 2017. Physicists and engineers use the phrase "order of magnitude" to refer to the smallest power of ten needed to represent a quantity.
↑ Shaalaa.com. "Answer the following question. Describe what is meant by order of magnitude. - Physics | Shaalaa.com". www.shaalaa.com. Retrieved 2023-06-04.
↑ Gibney, Elizabeth (2022). "How many yottabytes in a quettabyte? Extreme numbers get new names". Nature. doi:10.1038/d41586-022-03747-9. PMID 36400954. S2CID 253671538 . Retrieved 20 November 2022.

External links

The Scale of the Universe 2 Interactive tool from Planck length 10⁻³⁵ meters to universe size 10²⁷
Cosmos – an Illustrated Dimensional Journey from microcosmos to macrocosmos – from Digital Nature Agency
Powers of 10, a graphic animated illustration that starts with a view of the Milky Way at 10²³ meters and ends with subatomic particles at 10⁻¹⁶ meters.
What is Order of Magnitude?

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Brians, Paus. "Orders of Magnitude" . Retrieved 9 May 2013.

[2] "Order of Magnitude". Wolfram MathWorld. Retrieved 3 January 2017. Physicists and engineers use the phrase "order of magnitude" to refer to the smallest power of ten needed to represent a quantity.

[3] Shaalaa.com. "Answer the following question. Describe what is meant by order of magnitude. - Physics | Shaalaa.com". www.shaalaa.com. Retrieved 2023-06-04.

[4] Gibney, Elizabeth (2022). "How many yottabytes in a quettabyte? Extreme numbers get new names". Nature. doi:10.1038/d41586-022-03747-9. PMID 36400954. S2CID 253671538 . Retrieved 20 November 2022.

[1]

[2]

[3]

[4]

v t e Orders of magnitude
Quantity	Acceleration Angular momentum Area Bit rate Charge Computing Current Data Density Energy / Energy density Entropy Force Frequency Illuminance Length Luminance Magnetic field Mass Molarity Numbers Power Pressure Probability Radiation Sound pressure Specific heat capacity Speed Temperature Torque Time Voltage Volume
See also	Back-of-the-envelope calculation Best-selling electronic devices Fermi problem Powers of 10 and decades 10th 100th 1000000th Metric (SI) prefix Macroscopic scale Microscopic scale
Related	Astronomical system of units Earth's location in the Universe Cosmic View (1957 book) To the Moon and Beyond (1964 film) Cosmic Zoom (1968 film) Powers of Ten (1968 and 1977 films) Cosmic Voyage (1996 documentary) The Scale of the Universe (2010) Cosmic Eye (2012)
Category