| Agnibesa punctilinearia | |
|---|---|
Scientific classification  | |
| Domain: | Eukaryota |
| Kingdom: | Animalia |
| Phylum: | Arthropoda |
| Class: | Insecta |
| Order: | Lepidoptera |
| Family: | Geometridae |
| Genus: | Agnibesa |
| Species: | A. punctilinearia |
| Binomial name | |
| Agnibesa punctilinearia | |
| Synonyms | |
| |
Agnibesa punctilinearia is a moth in the family Geometridae. It is found in Western China. [2]
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of f and g. More precisely, if is the function such that for every x, then the chain rule is, in Lagrange's notation,
In mathematics, convolution is a mathematical operation on two functions that produces a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result. The integral is evaluated for all values of shift, producing the convolution function.
G, or g, is the seventh letter in the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is gee, plural gees.
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point is the "direction and rate of fastest increase". If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to maximize a function by gradient ascent. In coordinate-free terms, the gradient of a function may be defined by:
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In mathematical physics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.
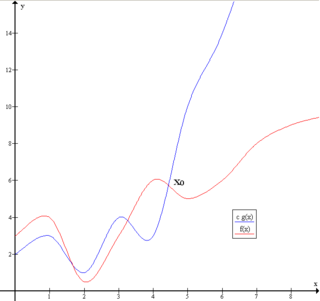
Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by German mathematicians Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for Ordnung, meaning the order of approximation.
In physics and mathematics, the Fourier transform (FT) is a transform that converts a function into a form that describes the frequencies present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into terms of the intensity of its constituent pitches.
The orbital period is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.
In chemistry, the molar mass of a chemical compound is defined as the ratio between the mass and the amount of substance of any sample of said compound. The molar mass is a bulk, not molecular, property of a substance. The molar mass is an average of many instances of the compound, which often vary in mass due to the presence of isotopes. Most commonly, the molar mass is computed from the standard atomic weights and is thus a terrestrial average and a function of the relative abundance of the isotopes of the constituent atoms on Earth. The molar mass is appropriate for converting between the mass of a substance and the amount of a substance for bulk quantities.
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.
In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as
Agnibesa is a genus of moths in the family Geometridae.
Plesiomorpha is a monotypic moth genus in the family Geometridae described by Warren in 1898.
Agnibesa pictaria is a moth in the family Geometridae first described by Frederic Moore in 1888. It is found in India, Nepal and China.
Agnibesa plumbeolineata is a moth in the family Geometridae first described by George Hampson in 1895. It is found in Sikkim in India and in China.
Agnibesa recurvilineata is a moth in the family Geometridae first described by Frederic Moore in 1888. It is found in Darjeeling in India, in western China and Nepal.
Agnibesa venusta is a moth in the family Geometridae first described by William Warren in 1897. It is found in Sikkim in India, Nepal and China.
Agnibesa pleopictaria is a moth in the family Geometridae first described by Dayong Xue in 1999. It is found in India.
 | This Asthenini moth related article is a stub. You can help Wikipedia by expanding it. |