An electronic oscillator is an electronic circuit that produces a periodic, oscillating or alternating current (AC) signal, usually a sine wave, square wave or a triangle wave, powered by a direct current (DC) source. Oscillators are found in many electronic devices, such as radio receivers, television sets, radio and television broadcast transmitters, computers, computer peripherals, cellphones, radar, and many other devices.
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:

Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms.

In mechanics and physics, simple harmonic motion is a special type of periodic motion an object experiences due to a restoring force whose magnitude is directly proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely.
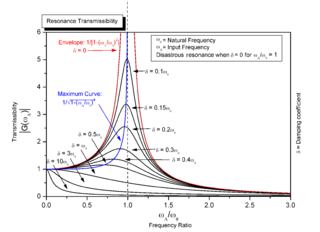
Resonance is the phenomenon, pertaining to oscillatory dynamical systems, wherein amplitude rises are caused by an external force with time-varying amplitude with the same frequency of variation as the natural frequency of the system. The amplitude rises that occur are a result of the fact that applied external forces at the natural frequency entail a net increase in mechanical energy of the system.
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. However, photons are fundamental particles that can be individually detected, whereas phonons, being quasiparticles, are an emergent phenomenon.
In physics and engineering, the quality factor or Q factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation. Q factor is alternatively defined as the ratio of a resonator's centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results. Higher Q indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high Q, while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer.

A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. These fixed frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge, or molecule, has a set of normal modes and their natural frequencies that depend on its structure, materials and boundary conditions.
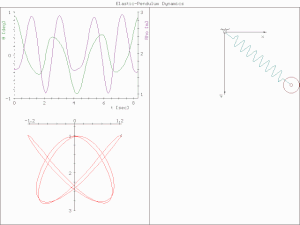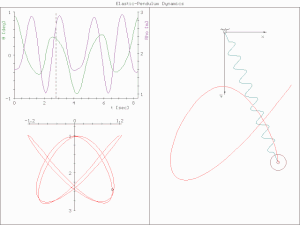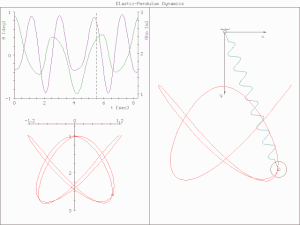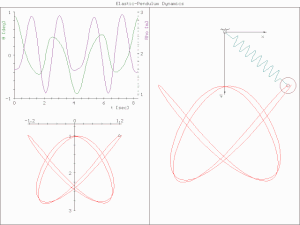
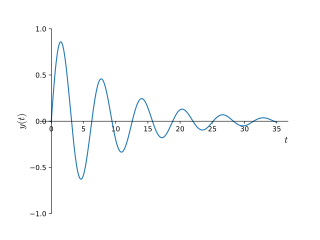
In physics, complex harmonic motion is a complicated realm based on the simple harmonic motion. The word "complex" refers to different situations. Unlike simple harmonic motion, which is regardless of air resistance, friction, etc., complex harmonic motion often has additional forces to dissipate the initial energy and lessen the speed and amplitude of an oscillation until the energy of the system is totally drained and the system comes to rest at its equilibrium point.
In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include viscous damping in a fluid, surface friction, radiation, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes. Damping is not to be confused with friction, which is a type of dissipative force acting on a system. Friction can cause or be a factor of damping.

The Duffing equation, named after Georg Duffing (1861–1944), is a non-linear second-order differential equation used to model certain damped and driven oscillators. The equation is given by

Mechanical resonance is the tendency of a mechanical system to respond at greater amplitude when the frequency of its oscillations matches the system's natural frequency of vibration closer than it does other frequencies. It may cause violent swaying motions and potentially catastrophic failure in improperly constructed structures including bridges, buildings and airplanes. This is a phenomenon known as resonance disaster.

A parametric oscillator is a driven harmonic oscillator in which the oscillations are driven by varying some parameters of the system at some frequencies, typically different from the natural frequency of the oscillator. A simple example of a parametric oscillator is a child pumping a playground swing by periodically standing and squatting to increase the size of the swing's oscillations. The child's motions vary the moment of inertia of the swing as a pendulum. The "pump" motions of the child must be at twice the frequency of the swing's oscillations. Examples of parameters that may be varied are the oscillator's resonance frequency and damping .
A mechanical amplifier or a mechanical amplifying element is a linkage mechanism that amplifies the magnitude of mechanical quantities such as force, displacement, velocity, acceleration and torque in linear and rotational systems. In some applications, mechanical amplification induced by nature or unintentional oversights in man-made designs can be disastrous, causing situations such as the 1940 Tacoma Narrows Bridge collapse. When employed appropriately, it can help to magnify small mechanical signals for practical applications.
In the physics of coupled oscillators, antiresonance, by analogy with resonance, is a pronounced minimum in the amplitude of an oscillator at a particular frequency, accompanied by a large, abrupt shift in its oscillation phase. Such frequencies are known as the system's antiresonant frequencies, and at these frequencies the oscillation amplitude can drop to almost zero. Antiresonances are caused by destructive interference, for example between an external driving force and interaction with another oscillator.

Vibration is a mechanical phenomenon whereby oscillations occur about an equilibrium point. Vibration may be deterministic if the oscillations can be characterised precisely, or random if the oscillations can only be analysed statistically.
In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude. The mixing of modes in non-linear systems is termed resonant interaction.

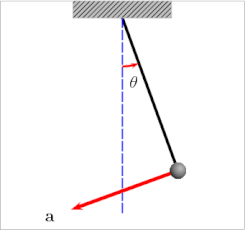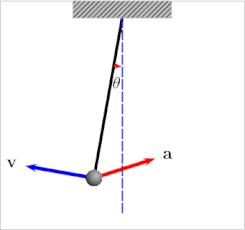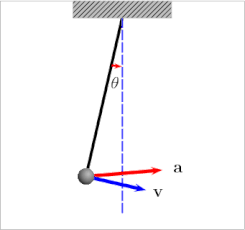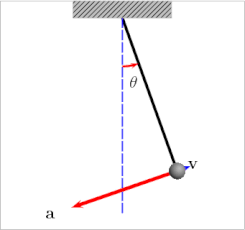
Kapitza's pendulum or Kapitza pendulum is a rigid pendulum in which the pivot point vibrates in a vertical direction, up and down. It is named after Russian Nobel laureate physicist Pyotr Kapitza, who in 1951 developed a theory which successfully explains some of its unusual properties. The unique feature of the Kapitza pendulum is that the vibrating suspension can cause it to balance stably in an inverted position, with the bob above the suspension point. In the usual pendulum with a fixed suspension, the only stable equilibrium position is with the bob hanging below the suspension point; the inverted position is a point of unstable equilibrium, and the smallest perturbation moves the pendulum out of equilibrium. In nonlinear control theory the Kapitza pendulum is used as an example of a parametric oscillator that demonstrates the concept of "dynamic stabilization".

Cavity optomechanics is a branch of physics which focuses on the interaction between light and mechanical objects on low-energy scales. It is a cross field of optics, quantum optics, solid-state physics and materials science. The motivation for research on cavity optomechanics comes from fundamental effects of quantum theory and gravity, as well as technological applications.
Rayleigh–Lorentz pendulum is a simple pendulum, but subjected to a slowly varying frequency due to an external action, named after Lord Rayleigh and Hendrik Lorentz. This problem formed the basis for the concept of adiabatic invariants in mechanics. On account of the slow variation of frequency, it is shown that the ratio of average energy to frequency is constant.