In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colours) of a sufficiently large complete graph. To demonstrate the theorem for two colours (say, blue and red), let r and s be any two positive integers. Ramsey's theorem states that there exists a least positive integer R(r, s) for which every blue-red edge colouring of the complete graph on R(r, s) vertices contains a blue clique on r vertices or a red clique on s vertices. (Here R(r, s) signifies an integer that depends on both r and s.)

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

Paul D. Seymour is a British mathematician known for his work in discrete mathematics, especially graph theory. He was responsible for important progress on regular matroids and totally unimodular matrices, the four colour theorem, linkless embeddings, graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture. Many of his recent papers are available from his website.

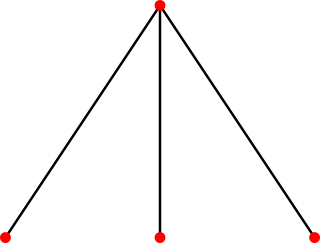
In the mathematical discipline of graph theory, a wheel graph is a graph formed by connecting a single universal vertex to all vertices of a cycle. A wheel graph with n vertices can also be defined as the 1-skeleton of an (n – 1)-gonal pyramid.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.
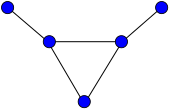
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

Maria Chudnovsky is an Israeli-American mathematician working on graph theory and combinatorial optimization. She is a 2012 MacArthur Fellow.
András Hajnal was a professor of mathematics at Rutgers University and a member of the Hungarian Academy of Sciences known for his work in set theory and combinatorics.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that

In the mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal in 1970. It is the smallest graph that is triangle-free, 4-regular, and 4-chromatic.

In the mathematical field of graph theory, the friendship graphFn is a planar, undirected graph with 2n + 1 vertices and 3n edges.
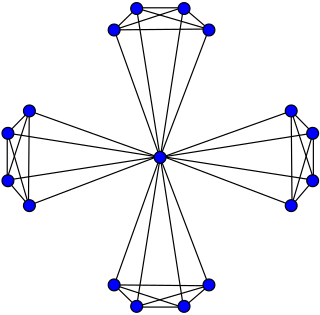
In the mathematical field of graph theory, the windmill graphWd(k,n) is an undirected graph constructed for k ≥ 2 and n ≥ 2 by joining n copies of the complete graph Kk at a shared universal vertex. That is, it is a 1-clique-sum of these complete graphs.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.
In graph theory, a branch of mathematics, the Erdős–Hajnal conjecture states that families of graphs defined by forbidden induced subgraphs have either large cliques or large independent sets. It is named for Paul Erdős and András Hajnal, who first posed it as an open problem in a paper from 1977.
In graph theory, a -bounded family of graphs is one for which there is some function such that, for every integer the graphs in with can be colored with at most colors. The function is called a -binding function for . These concepts and their notations were formulated by András Gyárfás. The use of the Greek letter chi in the term -bounded is based on the fact that the chromatic number of a graph is commonly denoted . An overview of the area can be found in a survey of Alex Scott and Paul Seymour.
In graph theory, the Gyárfás–Sumner conjecture asks whether, for every tree and complete graph , the graphs with neither nor as induced subgraphs can be properly colored using only a constant number of colors. Equivalently, it asks whether the -free graphs are -bounded. It is named after András Gyárfás and David Sumner, who formulated it independently in 1975 and 1981 respectively. It remains unproven.