Computation of radiowave attenuation in the atmosphere

Last updated May 04, 2023

The computation of radiowave attenuation in the atmosphere is a series of radio propagation models and methods to estimate the path loss due to attenuation of the signal passing through the atmosphere by the absorption of its different components. There are many well-known facts on the phenomenon and qualitative treatments in textbooks.^[1] A document published by the International Telecommunication Union (ITU) ^[2] provides some basis for a quantitative assessment of the attenuation. That document describes a simplified model along with semi-empirical formulas based on data fitting. It also recommended an algorithm to compute the attenuation of radiowave propagation in the atmosphere. NASA also published a study on a related subject.^[3] Free software from CNES based on ITU-R recommendations is available for download and is available to the public.

The model and the ITU recommendation

Derivation of the optical invariant, a measure of the light propagating through an optical system. Optinv.png — Derivation of the optical invariant, a measure of the light propagating through an optical system.

The document ITU-R pp. 676–78 of the ITU-R section considers the atmosphere as being divided into spherical homogeneous layers; each layer has a constant refraction index. By the use of trigonometry, a couple of formulas and an algorithm were derived.

Through the use of an invariant, the same results can be directly derived:

An incident ray at A under the angle Φ hits the layer B at the angle θ. From basic Euclidean geometry:

|CK|=R\sin u=r\sin \theta .

By Snell's law:

n_{1}\sin \Phi =n_{2}\sin u,

so that

n_{1}R\sin \Phi =n_{2}r\sin \theta =INV

Notes:

One proof^[1] starts from the Fermat's principle. As a result, one gets proof of the Snell's law along with this invariance. This invariant is valid in a more general situation; the spherical radius is then replaced by the radius of curvature at points along the ray. It is also used in equation (4) of the 2005 NASA's report^[3] in an application of satellite tracking.
The assumption of the refraction index varying with the latitude is not strictly compatible with the notion of layers. However the variation of the index is very small, this point is usually ignored in practice.

The ITU recommended algorithm consists of launching a ray from a radio source, then at each step, a layer is chosen and a new incidence angle is then computed. The process is iterated until the altitude of the target is reached. At each step, the covered distance dL is multiplied by a specific attenuation coefficient g expressed in dB/km. All the increments g dL are added to provide the total attenuation.

Note that the algorithm does not guaranty that the target is actually reached. For this, a much harder boundary value problem would have to be solved.

The eikonal equation

This equation is discussed in the references.^[4]^[5]^[6] The equation is highly non-linear. Given that a smooth data fitting curve n(altitude) is provided by the ITU^[7] for the refraction index n, and that the values of n differs from 1 only by something of the order 10⁻⁴, a numerical solution of the eikonal equation can be considered. Usually the equation is presented under the self-adjoint form, a more tractable equation for the ray head position vector r^[6] is given in generic parametric form:

{\ddot {\mathbf {r} }}=n\operatorname {grad} n

Implementations

Three implementations to compute the attenuations exist:

Take the ray to be a straight line.
Use the optical invariant and apply the ITU recommendation.^[2]
Solve the eikonal equation.

The first two are only of 1st order approximation (see Orders of approximation). For the eikonal equation, many numerical schemes are available.^[6] Here only a simple second order scheme was chosen. For most standard configurations of source-target, the three methods differ little from each other. It is only in the case of rays grazing the ground that the differences are meaningful. The following was used for testing:

At the latitude of 10°, when a ray starts at 5 km altitude with an elevation angle of −1° to hit a target at the same longitude but at latitude 8.84° and altitude 30 km. At 22.5 GHz, the results are:

The linear path is the highest on the figure, the eikonal is the lowest. The3methods.png — The linear path is the highest on the figure, the eikonal is the lowest.

dB	implementation	distance covered	finale altitude
30.27	Eikonal	761.11	30.06
29.20	Optical invariant	754.24	30.33
23.43	Linear	Trace Off

Note that 22.5 GHz is not a practical frequency^[1] but it is the most suitable for algorithms comparison. In the table, the first column gives the results in dB, the third gives the distance covered and the last gives the final altitude. Distances are in km. From the altitude 30 km up, the attenuation is negligible. The paths of the three are plotted:

Note: A MATLAB version for the uplink (Telecommunications link) is available from the ITU^[2]

The boundary value problem

When a point S communicates with a point T, the orientation of the ray is specified by an elevation angle. In a naïve way, the angle can be given by tracing a straight line from S to T. This specification does not guarantee that the ray will reach T: the variation of refraction index bends the ray trajectory. The elevation angle has to be modified^[3] to take into account the bending effect.

For the eikonal equation, this correction can be done by solving a boundary value problem. As the equation is of second order, the problem is well defined. In spite of the lack of a firm theoretical basis for the ITU method, a trial-error by dichotomy (or binary search) can also be used. The next figure shows the results of numerical simulations.

The curve labeled as bvp is the trajectory found by correcting the elevation angle. The other two are from a fixed step and a variable step (chosen in accordance with the ITU recommendations^[6]) solutions without the elevation angle correction. The nominal elevation angle for this case is −0.5-degree. The numerical results obtained at 22.5 GHz were:

	Attenuation	Elevation angle
ITU steps	15.40	−0.50°
Fix step	15.12	−0.50°
BVP	11.33	−0.22°

Note the way the solution bvp bends over the straight line. A consequence of this property is that the ray can reach locations situated below the horizon of S. This is consistent with observations.^[8] The trajectory is a Concave function is a consequence of the fact that the gradient of the refraction index is negative, so the Eikonal equation implies that the second derivative of the trajectory is negative. From the point where the ray is parallel to ground, relative to the chosen coordinates, the ray goes down but relative to ground level, the ray goes up.

Often engineers are interested in finding the limits of a system. In this case, a simple idea is to try some low elevation angle and let the ray reach the desired altitude. This point of view has a problem: if suffice to take the angle for which the ray has a tangent point of lowest altitude. For instance with the case of a source at 5 km altitude, of nominal elevation angle −0.5-degree and the target is at 30 km altitude; the attenuation found by the boundary value method is 11.33 dB. The previous point of view of worst case leads to an elevation angle of −1.87-degree and an attenuation of 170.77 dB. With this kind of attenuation, every system would be unusable! It was found also for this case that with the nominal elevation angle, the distance of the tangent point to ground is 5.84 km; that of the worst case is 2.69 km. The nominal distance from source to target is 6383.84 km; for the worst case, it is 990.36 km.

There are many numerical methods to solve boundary value problems.^[9] For the Eikonal equation, due to the good behavior of the refraction index just a simple Shooting method can be used.

Related Research Articles

The ionosphere is the ionized part of the upper atmosphere of Earth, from about 48 km (30 mi) to 965 km (600 mi) above sea level, a region that includes the thermosphere and parts of the mesosphere and exosphere. The ionosphere is ionized by solar radiation. It plays an important role in atmospheric electricity and forms the inner edge of the magnetosphere. It has practical importance because, among other functions, it influences radio propagation to distant places on Earth. It also affects GPS signals that travel through this layer.

$Refractive index Ratio of the speed of light in vacuum to that in the medium$

In optics, the refractive index of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.

$Refraction Physical phenomenon relating to the direction of waves$

In physics, refraction is the redirection of a wave as it passes from one medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commonly observed phenomenon, but other waves such as sound waves and water waves also experience refraction. How much a wave is refracted is determined by the change in wave speed and the initial direction of wave propagation relative to the direction of change in speed.

$Total internal reflection Reflection of a wave from a boundary between two media (rather than refraction)$

In physics, total internal reflection (TIR) is the phenomenon in which waves arriving at the interface (boundary) from one medium to another are not refracted into the second ("external") medium, but completely reflected back into the first ("internal") medium. It occurs when the second medium has a higher wave speed than the first, and the waves are incident at a sufficiently oblique angle on the interface. For example, the water-to-air surface in a typical fish tank, when viewed obliquely from below, reflects the underwater scene like a mirror with no loss of brightness (Fig. 1).

In telecommunications, an atmospheric duct is a horizontal layer in the lower atmosphere in which the vertical refractive index gradients are such that radio signals are guided or ducted, tend to follow the curvature of the Earth, and experience less attenuation in the ducts than they would if the ducts were not present. The duct acts as an atmospheric dielectric waveguide and limits the spread of the wavefront to only the horizontal dimension.

In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one material to another, provided there is no refractive power at the interface. The exact definition of the term varies slightly between different areas of optics. Numerical aperture is commonly used in microscopy to describe the acceptance cone of an objective, and in fiber optics, in which it describes the range of angles within which light that is incident on the fiber will be transmitted along it.

Path loss, or path attenuation, is the reduction in power density (attenuation) of an electromagnetic wave as it propagates through space. Path loss is a major component in the analysis and design of the link budget of a telecommunication system.

$Snell's law Formula for refraction angles$

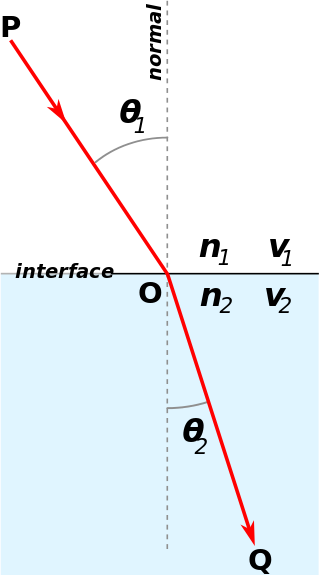
Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index.

Line-of-sight propagation is a characteristic of electromagnetic radiation or acoustic wave propagation which means waves travel in a direct path from the source to the receiver. Electromagnetic transmission includes light emissions traveling in a straight line. The rays or waves may be diffracted, refracted, reflected, or absorbed by the atmosphere and obstructions with material and generally cannot travel over the horizon or behind obstacles.

Radio propagation is the behavior of radio waves as they travel, or are propagated, from one point to another in vacuum, or into various parts of the atmosphere. As a form of electromagnetic radiation, like light waves, radio waves are affected by the phenomena of reflection, refraction, diffraction, absorption, polarization, and scattering. Understanding the effects of varying conditions on radio propagation has many practical applications, from choosing frequencies for amateur radio communications, international shortwave broadcasters, to designing reliable mobile telephone systems, to radio navigation, to operation of radar systems.

In astronomy, air mass or airmass is a measure of the amount of air along the line of sight when observing a star or other celestial source from below Earth's atmosphere. It is formulated as the integral of air density along the light ray.

Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of rays. The ray in geometrical optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances.

An antireflective, antiglare or anti-reflection (AR) coating is a type of optical coating applied to the surface of lenses, other optical elements, and photovoltaic cells to reduce reflection. In typical imaging systems, this improves the efficiency since less light is lost due to reflection. In complex systems such as cameras, binoculars, telescopes, and microscopes the reduction in reflections also improves the contrast of the image by elimination of stray light. This is especially important in planetary astronomy. In other applications, the primary benefit is the elimination of the reflection itself, such as a coating on eyeglass lenses that makes the eyes of the wearer more visible to others, or a coating to reduce the glint from a covert viewer's binoculars or telescopic sight.

$Atmospheric refraction Deviation of light as it moves through the atmosphere$

Atmospheric refraction is the deviation of light or other electromagnetic wave from a straight line as it passes through the atmosphere due to the variation in air density as a function of height. This refraction is due to the velocity of light through air decreasing with increased density. Atmospheric refraction near the ground produces mirages. Such refraction can also raise or lower, or stretch or shorten, the images of distant objects without involving mirages. Turbulent air can make distant objects appear to twinkle or shimmer. The term also applies to the refraction of sound. Atmospheric refraction is considered in measuring the position of both celestial and terrestrial objects.

Non-line-of-sight (NLOS) radio propagation occurs outside of the typical line-of-sight (LOS) between the transmitter and receiver, such as in ground reflections. Near-line-of-sight conditions refer to partial obstruction by a physical object present in the innermost Fresnel zone.

The beam propagation method (BPM) is an approximation technique for simulating the propagation of light in slowly varying optical waveguides. It is essentially the same as the so-called parabolic equation (PE) method in underwater acoustics. Both BPM and the PE were first introduced in the 1970s. When a wave propagates along a waveguide for a large distance, rigorous numerical simulation is difficult. The BPM relies on approximate differential equations which are also called the one-way models. These one-way models involve only a first order derivative in the variable z and they can be solved as "initial" value problem. The "initial" value problem does not involve time, rather it is for the spatial variable z.

The air mass coefficient defines the direct optical path length through the Earth's atmosphere, expressed as a ratio relative to the path length vertically upwards, i.e. at the zenith. The air mass coefficient can be used to help characterize the solar spectrum after solar radiation has traveled through the atmosphere.

This is an index to articles about terms used in discussion of radio propagation.

Cladding in optical fibers is one or more layers of materials of lower refractive index in intimate contact with a core material of higher refractive index. The cladding causes light to be confined to the core of the fiber by total internal reflection at the boundary between the core and cladding. Light propagation within the cladding is typically suppressed for most fibers. However, some fibers can support cladding modes in which light propagates through the cladding as well as the core. Depending upon the quantity of modes that are supported, they are referred to as multi-mode fibers and single-mode fibers. Improving transmission through fibers by applying a cladding was discovered in 1953 by Dutch scientist Bram van Heel.

Geometrical acoustics or ray acoustics is a branch of acoustics that studies propagation of sound on the basis of the concept of acoustic rays, defined as lines along which the acoustic energy is transported. This concept is similar to geometrical optics, or ray optics, that studies light propagation in terms of optical rays. Geometrical acoustics is an approximate theory, valid in the limiting case of very small wavelengths, or very high frequencies. The principal task of geometrical acoustics is to determine the trajectories of sound rays. The rays have the simplest form in a homogeneous medium, where they are straight lines. If the acoustic parameters of the medium are functions of spatial coordinates, the ray trajectories become curvilinear, describing sound reflection, refraction, possible focusing, etc. The equations of geometric acoustics have essentially the same form as those of geometric optics. The same laws of reflection and refraction hold for sound rays as for light rays. Geometrical acoustics does not take into account such important wave effects as diffraction. However, it provides a very good approximation when the wavelength is very small compared to the characteristic dimensions of inhomogeneous inclusions through which the sound propagates.

References

1 2 3 Antennas and radiowave propagation. Robert E. Collin. McGraw-Hill College, 1985
1 2 3 ITU recommendation ITU-R pp. 676–78, 2009^{[ clarification needed ]}
1 2 3 http://trs-new.jpl.nasa.gov/dspace/handle/2014/41145 Archived 23 April 2010 at the Wayback Machine . NASA progress report
↑ Microwave and optical ray geometry. S. Cornbleet, Wiley, 1984
↑ Light transmission optics. Detrich Marcuse, Van Nostrand, 1982
1 2 3 4 Methods in Electromagnetic Wave Propagation. D. S. Jones, Oxford, 1987
↑ ITU recommendation ITU-R pp. 835–4, 2009^{[ clarification needed ]}
↑ ITU recommendation ITU-R pp. 834–36, 2007 ^{[ clarification needed ]}
↑ Initial Value Methods for Boundary Value Problems. Mayer. Academic Press, 1973

External links

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[ReferenceA-1] 1 2 3 Antennas and radiowave propagation. Robert E. Collin. McGraw-Hill College, 1985

[ReferenceC-2] 1 2 3 ITU recommendation ITU-R pp. 676–78, 2009^{[ clarification needed ]}

[ReferenceD-3] 1 2 3 http://trs-new.jpl.nasa.gov/dspace/handle/2014/41145 Archived 23 April 2010 at the Wayback Machine . NASA progress report

[4] Microwave and optical ray geometry. S. Cornbleet, Wiley, 1984

[5] Light transmission optics. Detrich Marcuse, Van Nostrand, 1982

[ReferenceB-6] 1 2 3 4 Methods in Electromagnetic Wave Propagation. D. S. Jones, Oxford, 1987

[7] ITU recommendation ITU-R pp. 835–4, 2009^{[ clarification needed ]}

[8] ITU recommendation ITU-R pp. 834–36, 2007 ^{[ clarification needed ]}

[ReferenceI-9] Initial Value Methods for Boundary Value Problems. Mayer. Academic Press, 1973

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]