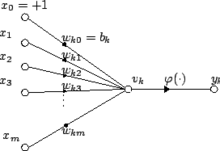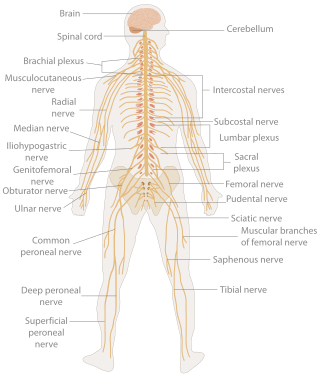
In biology, the nervous system is the highly complex part of an animal that coordinates its actions and sensory information by transmitting signals to and from different parts of its body. The nervous system detects environmental changes that impact the body, then works in tandem with the endocrine system to respond to such events. Nervous tissue first arose in wormlike organisms about 550 to 600 million years ago. In vertebrates, it consists of two main parts, the central nervous system (CNS) and the peripheral nervous system (PNS). The CNS consists of the brain and spinal cord. The PNS consists mainly of nerves, which are enclosed bundles of the long fibers, or axons, that connect the CNS to every other part of the body. Nerves that transmit signals from the brain are called motor nerves or efferent nerves, while those nerves that transmit information from the body to the CNS are called sensory nerves or afferent. Spinal nerves are mixed nerves that serve both functions. The PNS is divided into three separate subsystems, the somatic, autonomic, and enteric nervous systems. Somatic nerves mediate voluntary movement. The autonomic nervous system is further subdivided into the sympathetic and the parasympathetic nervous systems. The sympathetic nervous system is activated in cases of emergencies to mobilize energy, while the parasympathetic nervous system is activated when organisms are in a relaxed state. The enteric nervous system functions to control the gastrointestinal system. Both autonomic and enteric nervous systems function involuntarily. Nerves that exit from the cranium are called cranial nerves while those exiting from the spinal cord are called spinal nerves.

Neural Darwinism is a biological, and more specifically Darwinian and selectionist, approach to understanding global brain function, originally proposed by American biologist, researcher and Nobel-Prize recipient Gerald Maurice Edelman. Edelman's 1987 book Neural Darwinism introduced the public to the theory of neuronal group selection (TNGS) – which is the core theory underlying Edelman's explanation of global brain function.
Computational neuroscience is a branch of neuroscience which employs mathematics, computer science, theoretical analysis and abstractions of the brain to understand the principles that govern the development, structure, physiology and cognitive abilities of the nervous system.
An artificial neuron is a mathematical function conceived as a model of biological neurons in a neural network. Artificial neurons are the elementary units of artificial neural networks. The artificial neuron is a function that receives one or more inputs, applies weights to these inputs, and sums them to produce an output.

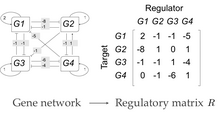
A generegulatory network (GRN) is a collection of molecular regulators that interact with each other and with other substances in the cell to govern the gene expression levels of mRNA and proteins which, in turn, determine the function of the cell. GRN also play a central role in morphogenesis, the creation of body structures, which in turn is central to evolutionary developmental biology (evo-devo).
Bio-inspired computing, short for biologically inspired computing, is a field of study which seeks to solve computer science problems using models of biology. It relates to connectionism, social behavior, and emergence. Within computer science, bio-inspired computing relates to artificial intelligence and machine learning. Bio-inspired computing is a major subset of natural computation.

Behavioral neuroscience, also known as biological psychology, biopsychology, or psychobiology, is the application of the principles of biology to the study of physiological, genetic, and developmental mechanisms of behavior in humans and other animals.

A neural circuit is a population of neurons interconnected by synapses to carry out a specific function when activated. Multiple neural circuits interconnect with one another to form large scale brain networks.
Neural engineering is a discipline within biomedical engineering that uses engineering techniques to understand, repair, replace, or enhance neural systems. Neural engineers are uniquely qualified to solve design problems at the interface of living neural tissue and non-living constructs.
Neuroinformatics is the field that combines informatics and neuroscience. Neuroinformatics is related with neuroscience data and information processing by artificial neural networks. There are three main directions where neuroinformatics has to be applied:

The Max Planck Institute of Experimental Medicine was a research institute of the Max Planck Society, located in Göttingen, Germany. On January 1, 2022, the institute merged with the Max Planck Institute for Biophysical Chemistry in Göttingen to form the Max Planck Institute for Multidisciplinary Sciences.

Spiking neural networks (SNNs) are artificial neural networks (ANN) that more closely mimic natural neural networks. In addition to neuronal and synaptic state, SNNs incorporate the concept of time into their operating model. The idea is that neurons in the SNN do not transmit information at each propagation cycle, but rather transmit information only when a membrane potential—an intrinsic quality of the neuron related to its membrane electrical charge—reaches a specific value, called the threshold. When the membrane potential reaches the threshold, the neuron fires, and generates a signal that travels to other neurons which, in turn, increase or decrease their potentials in response to this signal. A neuron model that fires at the moment of threshold crossing is also called a spiking neuron model.
GENESIS is a simulation environment for constructing realistic models of neurobiological systems at many levels of scale including: sub-cellular processes, individual neurons, networks of neurons, and neuronal systems. These simulations are “computer-based implementations of models whose primary objective is to capture what is known of the anatomical structure and physiological characteristics of the neural system of interest”. GENESIS is intended to quantify the physical framework of the nervous system in a way that allows for easy understanding of the physical structure of the nerves in question. “At present only GENESIS allows parallelized modeling of single neurons and networks on multiple-instruction-multiple-data parallel computers.” Development of GENESIS software spread from its home at Caltech to labs at the University of Texas at San Antonio, the University of Antwerp, the National Centre for Biological Sciences in Bangalore, the University of Colorado, the Pittsburgh Supercomputing Center, the San Diego Supercomputer Center, and Emory University.
In neuroscience and computer science, synaptic weight refers to the strength or amplitude of a connection between two nodes, corresponding in biology to the amount of influence the firing of one neuron has on another. The term is typically used in artificial and biological neural network research.
Models of neural computation are attempts to elucidate, in an abstract and mathematical fashion, the core principles that underlie information processing in biological nervous systems, or functional components thereof. This article aims to provide an overview of the most definitive models of neuro-biological computation as well as the tools commonly used to construct and analyze them.
Natural computing, also called natural computation, is a terminology introduced to encompass three classes of methods: 1) those that take inspiration from nature for the development of novel problem-solving techniques; 2) those that are based on the use of computers to synthesize natural phenomena; and 3) those that employ natural materials to compute. The main fields of research that compose these three branches are artificial neural networks, evolutionary algorithms, swarm intelligence, artificial immune systems, fractal geometry, artificial life, DNA computing, and quantum computing, among others.
Network of human nervous system comprises nodes that are connected by links. The connectivity may be viewed anatomically, functionally, or electrophysiologically. These are presented in several Wikipedia articles that include Connectionism, Biological neural network, Artificial neural network, Computational neuroscience, as well as in several books by Ascoli, G. A. (2002), Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011), Gerstner, W., & Kistler, W. (2002), and Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986) among others. The focus of this article is a comprehensive view of modeling a neural network. Once an approach based on the perspective and connectivity is chosen, the models are developed at microscopic, mesoscopic, or macroscopic (system) levels. Computational modeling refers to models that are developed using computing tools.
Compartmental modelling of dendrites deals with multi-compartment modelling of the dendrites, to make the understanding of the electrical behavior of complex dendrites easier. Basically, compartmental modelling of dendrites is a very helpful tool to develop new biological neuron models. Dendrites are very important because they occupy the most membrane area in many of the neurons and give the neuron an ability to connect to thousands of other cells. Originally the dendrites were thought to have constant conductance and current but now it has been understood that they may have active Voltage-gated ion channels, which influences the firing properties of the neuron and also the response of neuron to synaptic inputs. Many mathematical models have been developed to understand the electric behavior of the dendrites. Dendrites tend to be very branchy and complex, so the compartmental approach to understand the electrical behavior of the dendrites makes it very useful.
Soft computing is an umbrella term used to describe types of algorithms that produce approximate solutions to unsolvable high-level problems in computer science. Typically, traditional hard-computing algorithms heavily rely on concrete data and mathematical models to produce solutions to problems. Soft computing was coined in the late 20th century. During this period, revolutionary research in three fields greatly impacted soft computing. Fuzzy logic is a computational paradigm that entertains the uncertainties in data by using levels of truth rather than rigid 0s and 1s in binary. Next, neural networks which are computational models influenced by human brain functions. Finally, evolutionary computation is a term to describe groups of algorithm that mimic natural processes such as evolution and natural selection.

Synthetic Nervous System (SNS) is a computational neuroscience model that may be developed with the Functional Subnetwork Approach (FSA) to create biologically plausible models of circuits in a nervous system. The FSA enables the direct analytical tuning of dynamical networks that perform specific operations within the nervous system without the need for global optimization methods like genetic algorithms and reinforcement learning. The primary use case for a SNS is system control, where the system is most often a simulated biomechanical model or a physical robotic platform. An SNS is a form of a neural network much like artificial neural networks (ANNs), convolutional neural networks (CNN), and recurrent neural networks (RNN). The building blocks for each of these neural networks is a series of nodes and connections denoted as neurons and synapses. More conventional artificial neural networks rely on training phases where they use large data sets to form correlations and thus “learn” to identify a given object or pattern. When done properly this training results in systems that can produce a desired result, sometimes with impressive accuracy. However, the systems themselves are typically “black boxes” meaning there is no readily distinguishable mapping between structure and function of the network. This makes it difficult to alter the function, without simply starting over, or extract biological meaning except in specialized cases. The SNS method differentiates itself by using details of both structure and function of biological nervous systems. The neurons and synapse connections are intentionally designed rather than iteratively changed as part of a learning algorithm.