| Name | Plot | Function,  | Derivative of  , ,  | Range | Order of continuity |
|---|
| Identity |  |  |  |  |  |
| Binary step |  |  |  |  |  |
| Logistic, sigmoid, or soft step | 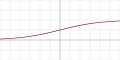 |  |  |  |  |
| Hyperbolic tangent (tanh) |  |  |  |  |  |
| Soboleva modified hyperbolic tangent (smht) |  |  | |  |  |
| Softsign | |  |  |  |  |
| Rectified linear unit (ReLU) [14] | 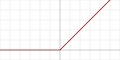 |  |  |  |  |
| Gaussian Error Linear Unit (GELU) [5] | 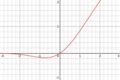 |  where where  is the gaussian error function. is the gaussian error function. |  where where  is the probability density function of standard gaussian distribution. is the probability density function of standard gaussian distribution. |  |  |
| Softplus [15] | 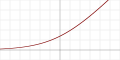 |  |  |  |  |
| Exponential linear unit (ELU) [16] | 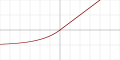 |  - with parameter

|  |  |  |
| Scaled exponential linear unit (SELU) [17] |  |  - with parameters
 and and 
|  |  |  |
| Leaky rectified linear unit (Leaky ReLU) [18] |  |  |  |  |  |
| Parametric rectified linear unit (PReLU) [19] |  |  - with parameter

|  |  |  |
| Rectified Parametric Sigmoid Units (flexible, 5 parameters) |  |  where  [20] [20] |  |  |  |
| Sigmoid linear unit (SiLU, [5] Sigmoid shrinkage, [21] SiL, [22] or Swish-1 [23] ) | 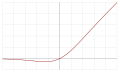 |  |  |  |  |
| Exponential Linear Sigmoid SquasHing (ELiSH) [24] |  |  |  |  |  |
| Gaussian |  |  |  |  |  |
| Sinusoid | |  |  |  |  |








































































































