In mathematics, a Coons patch, is a type of surface patch or manifold parametrization used in computer graphics to smoothly join other surfaces together, and in computational mechanics applications, particularly in finite element method and boundary element method, to mesh problem domains into elements.
Coons patches are named after Steven Anson Coons, and date to 1967. [1]
Given four space curves c0(s), c1(s), d0(t), d1(t) which meet at four corners c0(0) = d0(0), c0(1) = d1(0), c1(0) = d0(1), c1(1) = d1(1); linear interpolation can be used to interpolate between c0 and c1, that is
and between d0, d1
producing two ruled surfaces defined on the unit square.
The bilinear interpolation on the four corner points is another surface
A bilinearly blended Coons patch is the surface
Although the bilinear Coons patch exactly meets its four boundary curves, it does not necessarily have the same tangent plane at those curves as the surfaces to be joined, leading to creases in the joined surface along those curves. To fix this problem, the linear interpolation can be replaced with cubic Hermite splines with the weights chosen to match the partial derivatives at the corners. This forms a bicubically blended Coons patch.
In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points.
In the mathematical subfield of numerical analysis, a B-spline or basis spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. Any spline function of given degree can be expressed as a linear combination of B-splines of that degree. Cardinal B-splines have knots that are equidistant from each other. B-splines can be used for curve-fitting and numerical differentiation of experimental data.
In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling. As with Bézier curves, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive and, for many applications, mathematically convenient.
Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in computer graphics for representing curves and surfaces. It offers great flexibility and precision for handling both analytic and modeled shapes. It is a type of curve modeling, as opposed to polygonal modeling or digital sculpting. NURBS curves are commonly used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE). They are part of numerous industry-wide standards, such as IGES, STEP, ACIS, and PHIGS. Tools for creating and editing NURBS surfaces are found in various 3D graphics, rendering, and animation software packages.
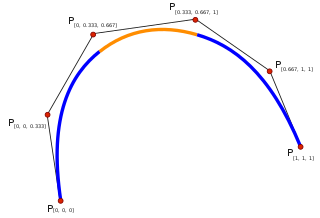
In mathematics, a spline is a function defined piecewise by polynomials. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree polynomials, while avoiding Runge's phenomenon for higher degrees.
In geometry, a point is an abstract idealization of an exact position, without size, in physical space, or its generalization to other kinds of mathematical spaces. As zero-dimensional objects, points are usually taken to be the fundamental indivisible elements comprising the space, of which one-dimensional curves, two-dimensional surfaces, and higher-dimensional objects consist; conversely, a point can be determined by the intersection of two curves or three surfaces, called a vertex or corner.
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types. Linear codes allow for more efficient encoding and decoding algorithms than other codes.
Steven Anson Coons was an early pioneer in the field of computer graphical methods. He was a professor at the Massachusetts Institute of Technology in the Mechanical Engineering Department. He was also a professor at Syracuse University after leaving MIT. Steven Coons had a vision of interactive computer graphics as a design tool to aid the engineer.
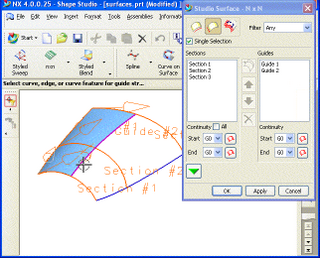
Freeform surface modelling is a technique for engineering freeform surfaces with a CAD or CAID system.
In computer science, partial order reduction is a technique for reducing the size of the state-space to be searched by a model checking or automated planning and scheduling algorithm. It exploits the commutativity of concurrently executed transitions that result in the same state when executed in different orders.
In numerical analysis, multivariate interpolation is interpolation on functions of more than one variable ; when the variates are spatial coordinates, it is also known as spatial interpolation.
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix is a matrix that represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation.
Isogeometric analysis is a computational approach that offers the possibility of integrating finite element analysis (FEA) into conventional NURBS-based CAD design tools. Currently, it is necessary to convert data between CAD and FEA packages to analyse new designs during development, a difficult task since the two computational geometric approaches are different. Isogeometric analysis employs complex NURBS geometry in the FEA application directly. This allows models to be designed, tested and adjusted in one go, using a common data set.
In numerical analysis, transfinite interpolation is a means to construct functions over a planar domain in such a way that they match a given function on the boundary. This method is applied in geometric modelling and in the field of finite element method.
Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence: The line integral of a vector field over a loop is equal to the surface integral of its curl over the enclosed surface. It is illustrated in the figure, where the direction of positive circulation of the bounding contour ∂Σ, and the direction n of positive flux through the surface Σ, are related by a right-hand-rule. For the right hand the fingers circulate along ∂Σ and the thumb is directed along n.
Ahlfors theory is a mathematical theory invented by Lars Ahlfors as a geometric counterpart of the Nevanlinna theory. Ahlfors was awarded one of the two very first Fields Medals for this theory in 1936.
In mathematics, differential forms on a Riemann surface are an important special case of the general theory of differential forms on smooth manifolds, distinguished by the fact that the conformal structure on the Riemann surface intrinsically defines a Hodge star operator on 1-forms without specifying a Riemannian metric. This allows the use of Hilbert space techniques for studying function theory on the Riemann surface and in particular for the construction of harmonic and holomorphic differentials with prescribed singularities. These methods were first used by Hilbert (1909) in his variational approach to the Dirichlet principle, making rigorous the arguments proposed by Riemann. Later Weyl (1940) found a direct approach using his method of orthogonal projection, a precursor of the modern theory of elliptic differential operators and Sobolev spaces. These techniques were originally applied to prove the uniformization theorem and its generalization to planar Riemann surfaces. Later they supplied the analytic foundations for the harmonic integrals of Hodge (1941). This article covers general results on differential forms on a Riemann surface that do not rely on any choice of Riemannian structure.
In algebraic topology and graph theory, graph homology describes the homology groups of a graph, where the graph is considered as a topological space. It formalizes the idea of the number of "holes" in the graph. It is a special case of a simplicial homology, as a graph is a special case of a simplicial complex. Since a finite graph is a 1-complex, the only non-trivial homology groups are the 0-th group and the 1-th group.
Weiqing Gu. "Surface Construction Schemes". Archived from the original on 2010-08-06. Retrieved 6 August 2010.
