
In geometry, a cube is a three-dimensional solid object bounded by six square faces. It has twelve edges and eight vertices. It can be represented as a rectangular cuboid with six square faces, or a parallelepiped with equal edges. It is an example of many type of solids: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a strictly convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two solids with such a property: the first solids are the pyramids, cupolas. and a rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. These solids are named after mathematicians Norman Johnson and Victor Zalgaller.
In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.

In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.

In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.

In geometry, the elongated square bipyramid is the polyhedron constructed by attaching two equilateral square pyramids onto a cube's faces that are opposite each other. It can also be seen as 4 lunes linked together with squares to squares and triangles to triangles. It is also been named the pencil cube or 12-faced pencil cube due to its shape.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
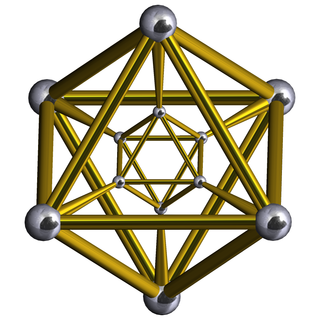
In geometry, an octahedral prism is a convex uniform 4-polytope. This 4-polytope has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.

In geometry, a simplicial polytope is a polytope whose facets are all simplices. For example, a simplicial polyhedron in three dimensions contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph.
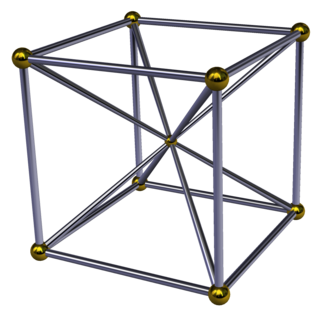
In 4-dimensional geometry, the cubic pyramid is bounded by one cube on the base and 6 square pyramid cells which meet at the apex. Since a cube has a circumradius divided by edge length less than one, the square pyramids can be made with regular faces by computing the appropriate height.
In geometry, a Hanner polytope is a convex polytope constructed recursively by Cartesian product and polar dual operations. Hanner polytopes are named after Olof Hanner, who introduced them in 1956.
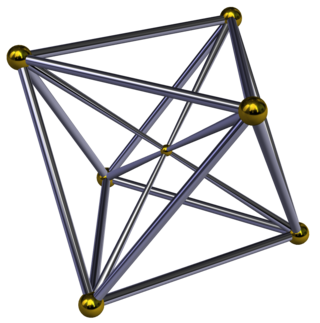
In 4-dimensional geometry, the octahedral pyramid is bounded by one octahedron on the base and 8 triangular pyramid cells which meet at the apex. Since an octahedron has a circumradius divided by edge length less than one, the triangular pyramids can be made with regular faces by computing the appropriate height.
In geometry, a Blind polytope is a convex polytope composed of regular polytope facets. The category was named after the German couple Gerd and Roswitha Blind, who described them in a series of papers beginning in 1979. It generalizes the set of semiregular polyhedra and Johnson solids to higher dimensions.

In 4-dimensional geometry, the tetrahedral bipyramid is the direct sum of a tetrahedron and a segment, {3,3} + { }. Each face of a central tetrahedron is attached with two tetrahedra, creating 8 tetrahedral cells, 16 triangular faces, 14 edges, and 6 vertices. A tetrahedral bipyramid can be seen as two tetrahedral pyramids augmented together at their base.














