Curved mirror

Reflections in a convex mirror. The photographer is seen reflected at top right

A curved mirror is a mirror with a curved reflecting surface. The surface may be either convex (bulging outward) or concave (recessed inward). Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices. The most common non-spherical type are parabolic reflectors, found in optical devices such as reflecting telescopes that need to image distant objects, since spherical mirror systems, like spherical lenses, suffer from spherical aberration. Distorting mirrors are used for entertainment. They have convex and concave regions that produce deliberately distorted images. They also provide highly magnified or highly diminished (smaller) images when the object is placed at certain distances.

Convex mirrors

A convex mirror diagram showing the focus, focal length, centre of curvature, principal axis, etc.

A convex mirror or diverging mirror is a curved mirror in which the reflective surface bulges towards the light source. ^[1] Convex mirrors reflect light outwards, therefore they are not used to focus light. Such mirrors always form a virtual image, since the focal point (F) and the centre of curvature (2F) are both imaginary points "inside" the mirror, that cannot be reached. As a result, images formed by these mirrors cannot be projected on a screen, since the image is inside the mirror. The image is smaller than the object, but gets larger as the object approaches the mirror.

A collimated (parallel) beam of light diverges (spreads out) after reflection from a convex mirror, since the normal to the surface differs at each spot on the mirror.

Uses

Convex mirror lets motorists see around a corner.

Detail of the convex mirror in the Arnolfini Portrait

The passenger-side mirror on a car is typically a convex mirror. In some countries, these are labeled with the safety warning "Objects in mirror are closer than they appear", to warn the driver of the convex mirror's distorting effects on distance perception. Convex mirrors are preferred in vehicles because they give an upright (not inverted), though diminished (smaller), image and because they provide a wider field of view as they are curved outwards.

These mirrors are often found in the hallways of various buildings (commonly known as "hallway safety mirrors"), including hospitals, hotels, schools, stores, and apartment buildings. They are usually mounted on a wall or ceiling where hallways intersect each other, or where they make sharp turns. They are useful for people to look at any obstruction they will face on the next hallway or after the next turn. They are also used on roads, driveways, and alleys to provide safety for road users where there is a lack of visibility, especially at curves and turns. ^[2]

Convex mirrors are used in some automated teller machines as a simple and handy security feature, allowing the users to see what is happening behind them. Similar devices are sold to be attached to ordinary computer monitors. Convex mirrors make everything seem smaller but cover a larger area of surveillance.

Round convex mirrors called Oeil de Sorcière (French for "sorcerer's eye") were a popular luxury item from the 15th century onwards, shown in many depictions of interiors from that time. ^[3] With 15th century technology, it was easier to make a regular curved mirror (from blown glass) than a perfectly flat one. They were also known as "bankers' eyes" due to the fact that their wide field of vision was useful for security. Famous examples in art include the Arnolfini Portrait by Jan van Eyck and the left wing of the Werl Altarpiece by Robert Campin. ^[4]

Image

A virtual image in a Christmas bauble.

The image on a convex mirror is always virtual (rays haven't actually passed through the image; their extensions do, like in a regular mirror), diminished (smaller), and upright (not inverted). As the object gets closer to the mirror, the image gets larger, until approximately the size of the object, when it touches the mirror. As the object moves away, the image diminishes in size and gets gradually closer to the focus, until it is reduced to a point in the focus when the object is at an infinite distance. These features make convex mirrors very useful: since everything appears smaller in the mirror, they cover a wider field of view than a normal plane mirror, so useful for looking at cars behind a driver's car on a road, watching a wider area for surveillance, etc.

Effect on image of object's position relative to mirror focal point (convex)

Object's position (S), focal point (F)	Image	Diagram
${\displaystyle S>F,\ S=F,\ S<F}$	Virtual Upright Reduced (diminished/smaller)

Concave mirrors

A concave mirror diagram showing the focus, focal length, centre of curvature, principal axis, etc.

A concave mirror, or converging mirror, has a reflecting surface that is recessed inward (away from the incident light). Concave mirrors reflect light inward to one focal point. They are used to focus light. Unlike convex mirrors, concave mirrors show different image types depending on the distance between the object and the mirror.

The mirrors are called "converging mirrors" because they tend to collect light that falls on them, refocusing parallel incoming rays toward a focus. This is because the light is reflected at different angles at different spots on the mirror as the normal to the mirror surface differs at each spot.

Uses

Concave mirrors are used in reflecting telescopes. ^[5] They are also used to provide a magnified image of the face for applying make-up or shaving. ^[6] In illumination applications, concave mirrors are used to gather light from a small source and direct it outward in a beam as in torches, headlamps and spotlights, or to collect light from a large area and focus it into a small spot, as in concentrated solar power. Concave mirrors are used to form optical cavities, which are important in laser construction. Some dental mirrors use a concave surface to provide a magnified image. The mirror landing aid system of modern aircraft carriers also uses a concave mirror.

Image

Effect on image of object's position relative to mirror focal point (concave)

Object's position (S), focal point (F)	Nature of Image	Diagram
${\displaystyle S<F}$ (Object between focal point and mirror)	Virtual Upright Magnified (larger)
${\displaystyle S=F}$ (Object at focal point)	Reflected rays are parallel and never meet, so no image is formed. In the limit where S approaches F, the image distance approaches infinity, and the image can be either real or virtual and either upright or inverted depending on whether S approaches F from its left or right side.
${\displaystyle F<S<2F}$ (Object between focus and centre of curvature)	Real image Inverted (vertically) Magnified (larger)
${\displaystyle S=2F}$ (Object at centre of curvature)	Real image Inverted (vertically) Same size Image formed at centre of curvature
${\displaystyle S>2F}$ (Object beyond centre of curvature)	Real image Inverted (vertically) Reduced (diminished/smaller) As the distance of the object increases, the image asymptotically approaches the focal point In the limit where S approaches infinity, the image size approaches zero as the image approaches F

Mirror shape

Most curved mirrors have a spherical profile. ^[7] These are the simplest to make, and it is the best shape for general-purpose use. Spherical mirrors, however, suffer from spherical aberration—parallel rays reflected from such mirrors do not focus to a single point. For parallel rays, such as those coming from a very distant object, a parabolic reflector can do a better job. Such a mirror can focus incoming parallel rays to a much smaller spot than a spherical mirror can. A toroidal reflector is a form of parabolic reflector which has a different focal distance depending on the angle of the mirror.

Analysis

Mirror equation, magnification, and focal length

The Gaussian mirror equation, also known as the mirror and lens equation, relates the object distance ${\displaystyle d_{\mathrm {o} }}$ and image distance ${\displaystyle d_{\mathrm {i} }}$ to the focal length ${\displaystyle f}$: ^[2]

${\displaystyle {\frac {1}{d_{\mathrm {o} }}}+{\frac {1}{d_{\mathrm {i} }}}={\frac {1}{f}}}$.

The sign convention used here is that the focal length is positive for concave mirrors and negative for convex ones, and ${\displaystyle d_{\mathrm {o} }}$ and ${\displaystyle d_{\mathrm {i} }}$ are positive when the object and image are in front of the mirror, respectively. (They are positive when the object or image is real.) ^[2]

For convex mirrors, if one moves the ${\displaystyle 1/d_{\mathrm {o} }}$ term to the right side of the equation to solve for ${\displaystyle 1/d_{\mathrm {i} }}$, then the result is always a negative number, meaning that the image distance is negative—the image is virtual, located "behind" the mirror. This is consistent with the behavior described above.

For concave mirrors, whether the image is virtual or real depends on how large the object distance is compared to the focal length. If the ${\displaystyle 1/f}$ term is larger than the ${\displaystyle 1/d_{\mathrm {o} }}$ term, then ${\displaystyle 1/d_{\mathrm {i} }}$ is positive and the image is real. Otherwise, the term is negative and the image is virtual. Again, this validates the behavior described above.

The magnification of a mirror is defined as the height of the image divided by the height of the object:

${\displaystyle m\equiv {\frac {h_{\mathrm {i} }}{h_{\mathrm {o} }}}=-{\frac {d_{\mathrm {i} }}{d_{\mathrm {o} }}}}$.

By convention, if the resulting magnification is positive, the image is upright. If the magnification is negative, the image is inverted (upside down).

Ray tracing

Main article: Ray tracing (physics)

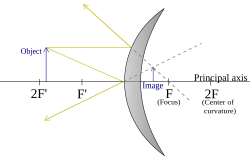
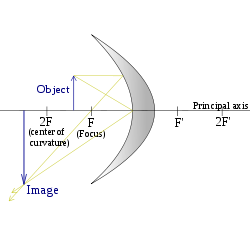
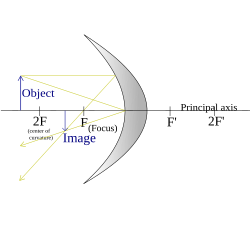
The image location and size can also be found by graphical ray tracing, as illustrated in the figures above. A ray drawn from the top of the object to the mirror surface vertex (where the optical axis meets the mirror) will form an angle with the optical axis. The reflected ray has the same angle to the axis, but on the opposite side (See Specular reflection).

A second ray can be drawn from the top of the object, parallel to the optical axis. This ray is reflected by the mirror and passes through its focal point. The point at which these two rays meet is the image point corresponding to the top of the object. Its distance from the optical axis defines the height of the image, and its location along the axis is the image location. The mirror equation and magnification equation can be derived geometrically by considering these two rays. A ray that goes from the top of the object through the focal point can be considered instead. Such a ray reflects parallel to the optical axis and also passes through the image point corresponding to the top of the object.

Ray transfer matrix of spherical mirrors

Further information: Ray transfer matrix analysis

The mathematical treatment is done under the paraxial approximation, meaning that under the first approximation a spherical mirror is a parabolic reflector. The ray matrix of a concave spherical mirror is shown here. The ${\displaystyle C}$ element of the matrix is ${\displaystyle -{\frac {1}{f}}}$, where ${\displaystyle f}$ is the focal point of the optical device.

Boxes 1 and 3 feature summing the angles of a triangle and comparing to π radians (or 180°). Box 2 shows the Maclaurin series of ${\displaystyle \arccos \left(-{\frac {r}{R}}\right)}$ up to order 1. The derivations of the ray matrices of a convex spherical mirror and a thin lens are very similar.

See also

• Alhazen's problem (reflection from a spherical mirror)
• Anamorphosis
• Concentrated solar power - a method of solar power generation using curved mirrors or arrays of mirrors
• Dioptre
• List of telescope parts and construction
• Optical power

References

1. Nayak, Sanjay K.; Bhuvana, K.P. (2012). Engineering Physics. New Delhi: Tata McGraw-Hill Education. p. 6.4. ISBN   9781259006449.
2. Hecht, Eugene (1987). "5.4.3". Optics (2nd ed.). Addison Wesley. pp. 160–1. ISBN   0-201-11609-X.
3. Venice Botteghe: Antiques, Bijouterie, Coffee, Cakes, Carpet, Glass Archived 2017-03-06 at the Wayback Machine
4. Lorne Campbell, National Gallery Catalogues (new series): The Fifteenth Century Netherlandish Paintings, pp. 178-179, 188-189, 1998, ISBN   1-85709-171-X
5. Joshi, Dhiren M. Living Science Physics 10. Ratna Sagar. ISBN   9788183322904. Archived from the original on 2018-01-18.
6. Sura's Year Book 2006 (English). Sura Books. ISBN   9788172541248. Archived from the original on 2018-01-18.
7. Al-Azzawi, Abdul (2006-12-26). Light and Optics: Principles and Practices. CRC Press. ISBN   9780849383144. Archived from the original on 2018-01-18.

External links

• Java applets to explore ray tracing for curved mirrors
• Concave mirrors — real images, Molecular Expressions Optical Microscopy Primer
• Spherical mirrors, online physics lab
• "Grinding the World's Largest Mirror" Popular Science, December 1935