Digital control

Last updated November 27, 2024

Digital control is a branch of control theory that uses digital computers to act as system controllers. Depending on the requirements, a digital control system can take the form of a microcontroller to an ASIC to a standard desktop computer. Since a digital computer is a discrete system, the Laplace transform is replaced with the Z-transform. Since a digital computer has finite precision (See quantization ), extra care is needed to ensure the error in coefficients, analog-to-digital conversion, digital-to-analog conversion, etc. are not producing undesired or unplanned effects.

Since the creation of the first digital computer in the early 1940s the price of digital computers has dropped considerably, which has made them key pieces to control systems because they are easy to configure and reconfigure through software, can scale to the limits of the memory or storage space without extra cost, parameters of the program can change with time (See adaptive control ) and digital computers are much less prone to environmental conditions than capacitors, inductors, etc.

Digital controller implementation

A digital controller is usually cascaded with the plant in a feedback system. The rest of the system can either be digital or analog.

Typically, a digital controller requires:

Analog-to-digital conversion to convert analog inputs to machine-readable (digital) format
Digital-to-analog conversion to convert digital outputs to a form that can be input to a plant (analog)
A program that relates the outputs to the inputs

Output program

Outputs from the digital controller are functions of current and past input samples, as well as past output samples - this can be implemented by storing relevant values of input and output in registers. The output can then be formed by a weighted sum of these stored values.

The programs can take numerous forms and perform many functions

A digital filter for low-pass filtering
A state space model of a system to act as a state observer
A telemetry system

Stability

Although a controller may be stable when implemented as an analog controller, it could be unstable when implemented as a digital controller due to a large sampling interval. During sampling the aliasing modifies the cutoff parameters. Thus the sample rate characterizes the transient response and stability of the compensated system, and must update the values at the controller input often enough so as to not cause instability.

When substituting the frequency into the z operator, regular stability criteria still apply to discrete control systems. Nyquist criteria apply to z-domain transfer functions as well as being general for complex valued functions. Bode stability criteria apply similarly. Jury criterion determines the discrete system stability about its characteristic polynomial.

Design of digital controller in s-domain

The digital controller can also be designed in the s-domain (continuous). The Tustin transformation can transform the continuous compensator to the respective digital compensator. The digital compensator will achieve an output that approaches the output of its respective analog controller as the sampling interval is decreased.

$s={\frac {2(z-1)}{T(z+1)}}$

Tustin transformation deduction

Tustin is the Padé_(1,1) approximation of the exponential function ${\begin{aligned}z&=e^{sT}\end{aligned}}$ :

{\begin{aligned}z&=e^{sT}\\&={\frac {e^{sT/2}}{e^{-sT/2}}}\\&\approx {\frac {1+sT/2}{1-sT/2}}\end{aligned}}

And its inverse

{\begin{aligned}s&={\frac {1}{T}}\ln(z)\\&={\frac {2}{T}}\left[{\frac {z-1}{z+1}}+{\frac {1}{3}}\left({\frac {z-1}{z+1}}\right)^{3}+{\frac {1}{5}}\left({\frac {z-1}{z+1}}\right)^{5}+{\frac {1}{7}}\left({\frac {z-1}{z+1}}\right)^{7}+\cdots \right]\\&\approx {\frac {2}{T}}{\frac {z-1}{z+1}}\\&={\frac {2}{T}}{\frac {1-z^{-1}}{1+z^{-1}}}\end{aligned}}

Digital control theory is the technique to design strategies in discrete time, (and/or) quantized amplitude (and/or) in (binary) coded form to be implemented in computer systems (microcontrollers, microprocessors) that will control the analog (continuous in time and amplitude) dynamics of analog systems. From this consideration many errors from classical digital control were identified and solved and new methods were proposed:

Marcelo Tredinnick and Marcelo Souza and their new type of analog-digital mapping^[1]^[2]^[3]
Yutaka Yamamoto and his "lifting function space model"^[4]
Alexander Sesekin and his studies about impulsive systems.^[5]
M.U. Akhmetov and his studies about impulsive and pulse control^[6]

Design of digital controller in z-domain

The digital controller can also be designed in the z-domain (discrete). The Pulse Transfer Function (PTF) $G(z)$ represents the digital viewpoint of the continuous process $G(s)$ when interfaced with appropriate ADC and DAC, and for a specified sample time $T$ is obtained as:^[7]

$G(z)={\frac {B(z)}{A(z)}}={\frac {(z-1)}{z}}Z{\biggl (}{\frac {G(s)}{s}}{\Biggr )}$

Where $Z()$ denotes z-Transform for the chosen sample time $T$ . There are many ways to directly design a digital controller $D(z)$ to achieve a given specification.^[7] For a type-0 system under unity negative feedback control, Michael Short and colleagues have shown that a relatively simple but effective method to synthesize a controller for a given (monic) closed-loop denominator polynomial $P(z)$ and preserve the (scaled) zeros of the PTF numerator $B(z)$ is to use the design equation:^[8]

$D(z)={\frac {k_{p}A(z)}{P(z)-k_{p}B(z)}}$

Where the scalar term $k_{p}=P(1)/B(1)$ ensures the controller $D(z)$ exhibits integral action, and a steady-state gain of unity is achieved in the closed-loop. The resulting closed-loop discrete transfer function from the z-Transform of reference input $R(z)$ to the z-Transform of process output $Y(z)$ is then given by:^[8]

${\frac {Y(z)}{R(z)}}={\frac {k_{p}B(z)}{P(z)}}$

Since process time delay manifests as leading co-efficient(s) of zero in the process PTF numerator $B(z)$ , the synthesis method above inherently yields a predictive controller if any such delay is present in the continuous plant.^[8]

Related Research Articles

The bilinear transform is used in digital signal processing and discrete-time control theory to transform continuous-time system representations to discrete-time and vice versa.

Linear filters process time-varying input signals to produce output signals, subject to the constraint of linearity. In most cases these linear filters are also time invariant in which case they can be analyzed exactly using LTI system theory revealing their transfer functions in the frequency domain and their impulse responses in the time domain. Real-time implementations of such linear signal processing filters in the time domain are inevitably causal, an additional constraint on their transfer functions. An analog electronic circuit consisting only of linear components will necessarily fall in this category, as will comparable mechanical systems or digital signal processing systems containing only linear elements. Since linear time-invariant filters can be completely characterized by their response to sinusoids of different frequencies, they are sometimes known as frequency filters.

In engineering, a transfer function of a system, sub-system, or component is a mathematical function that models the system's output for each possible input. It is widely used in electronic engineering tools like circuit simulators and control systems. In simple cases, this function can be represented as a two-dimensional graph of an independent scalar input versus the dependent scalar output. Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory.

In signal processing, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is typically an electronic circuit operating on continuous-time analog signals.

A phase-locked loop or phase lock loop (PLL) is a control system that generates an output signal whose phase is fixed relative to the phase of an input signal. Keeping the input and output phase in lockstep also implies keeping the input and output frequencies the same, thus a phase-locked loop can also track an input frequency. And by incorporating a frequency divider, a PLL can generate a stable frequency that is a multiple of the input frequency.

A proportional–integral–derivative controller is a feedback-based control loop mechanism commonly used to manage machines and processes that require continuous control and automatic adjustment. It is typically used in industrial control systems and various other applications where constant control through modulation is necessary without human intervention. The PID controller automatically compares the desired target value with the actual value of the system. The difference between these two values is called the error value, denoted as $.$

In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex valued frequency-domain representation.

<span class="mw-page-title-main">Root locus analysis</span> Stability criterion in control theory

In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a stability criterion in the field of classical control theory developed by Walter R. Evans which can determine stability of the system. The root locus plots the poles of the closed loop transfer function in the complex s-plane as a function of a gain parameter.

In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely.

Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response $that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response does become exactly zero at times for some finite, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as IIR systems or IIR filters .$

In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined in the overview below. These properties apply (exactly or approximately) to many important physical systems, in which case the response $y (t)$ of the system to an arbitrary input $x (t)$ can be found directly using convolution: $y (t) = (x * h)(t)$ where $h (t)$ is called the system's impulse response and ∗ represents convolution (not to be confused with multiplication). What's more, there are systematic methods for solving any such system (determining $h (t)$ ), whereas systems not meeting both properties are generally more difficult (or impossible) to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers.

Delta-sigma modulation is an oversampling method for encoding signals into low bit depth digital signals at a very high sample-frequency as part of the process of delta-sigma analog-to-digital converters (ADCs) and digital-to-analog converters (DACs). Delta-sigma modulation achieves high quality by utilizing a negative feedback loop during quantization to the lower bit depth that continuously corrects quantization errors and moves quantization noise to higher frequencies well above the original signal's bandwidth. Subsequent low-pass filtering for demodulation easily removes this high frequency noise and time averages to achieve high accuracy in amplitude which can be ultimately encoded as pulse-code modulation (PCM).

A lead–lag compensator is a component in a control system that improves an undesirable frequency response in a feedback and control system. It is a fundamental building block in classical control theory.

In applied mathematics, the starred transform, or star transform, is a discrete-time variation of the Laplace transform, so-named because of the asterisk or "star" in the customary notation of the sampled signals. The transform is an operator of a continuous-time function $, which is transformed to a function in the following manner:$

A switched capacitor (SC) is an electronic circuit that implements a function by moving charges into and out of capacitors when electronic switches are opened and closed. Usually, non-overlapping clock signals are used to control the switches, so that not all switches are closed simultaneously. Filters implemented with these elements are termed switched-capacitor filters, which depend only on the ratios between capacitances and the switching frequency, and not on precise resistors. This makes them much more suitable for use within integrated circuits, where accurately specified resistors and capacitors are not economical to construct, but accurate clocks and accurate relative ratios of capacitances are economical.

In discrete-time control theory, the dead-beat control problem consists of finding what input signal must be applied to a system in order to bring the output to the steady state in the smallest number of time steps.

The zero-order hold (ZOH) is a mathematical model of the practical signal reconstruction done by a conventional digital-to-analog converter (DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.

Two dimensional filters have seen substantial development effort due to their importance and high applicability across several domains. In the 2-D case the situation is quite different from the 1-D case, because the multi-dimensional polynomials cannot in general be factored. This means that an arbitrary transfer function cannot generally be manipulated into a form required by a particular implementation. The input-output relationship of a 2-D IIR filter obeys a constant-coefficient linear partial difference equation from which the value of an output sample can be computed using the input samples and previously computed output samples. Because the values of the output samples are fed back, the 2-D filter, like its 1-D counterpart, can be unstable.

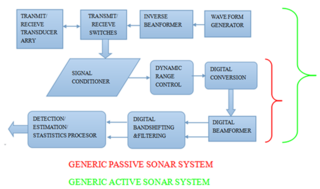
Sonar systems are generally used underwater for range finding and detection. Active sonar emits an acoustic signal, or pulse of sound, into the water. The sound bounces off the target object and returns an echo to the sonar transducer. Unlike active sonar, passive sonar does not emit its own signal, which is an advantage for military vessels. But passive sonar cannot measure the range of an object unless it is used in conjunction with other passive listening devices. Multiple passive sonar devices must be used for triangulation of a sound source. No matter whether active sonar or passive sonar, the information included in the reflected signal can not be used without technical signal processing. To extract the useful information from the mixed signal, some steps are taken to transfer the raw acoustic data.

Classical control theory is a branch of control theory that deals with the behavior of dynamical systems with inputs, and how their behavior is modified by feedback, using the Laplace transform as a basic tool to model such systems.

References

↑ "Referência Completa". mtc-m18.sid.inpe.br. Archived from the original on March 5, 2012.
↑ "Discrete attitude control of artificial satellites with flexible appendages" (PDF). mtc-m05.sid.inpe.br. Archived from the original (PDF) on 6 July 2011. Retrieved 12 January 2022.
↑ "An Analytical Approach for Discrete Controllers Design Using a New S-Z Mapping with Two Tuning Parameters". www.sae.org. Archived from the original on 13 January 2013. Retrieved 27 January 2022.
↑ Yamamoto, Yutaka (1996). "A Retrospective View on Sampled-Data - Control Systems" (PDF). Kyoto University . Archived from the original (PDF) on 22 July 2011. Retrieved 12 January 2022.
↑ Zavalishchin, S. T.; Sesekin, A. N. (28 February 1997). Dynamic Impulse Systems: Theory and Applications. Springer. ISBN 0792343948.
↑ "Author page". Association for Computing Machinery . Retrieved 2009-03-20.^{[ permanent dead link ‍]}
1 2 Åström, Karl J.; Wittenmark, Björn (2013-06-13). Computer-Controlled Systems: Theory and Design, Third Edition. Courier Corporation. ISBN 978-0-486-28404-0.
1 2 3 Short, Michael; Abugchem, Fathi; Abrar, Usama (2015-02-11). "Dependable Control for Wireless Distributed Control Systems". Electronics. 4 (4): 857–878. doi: 10.3390/electronics4040857 .

FRANKLIN, G.F.; POWELL, J.D., Emami-Naeini, A., Digital Control of Dynamical Systems, 3rd Ed (1998). Ellis-Kagle Press, Half Moon Bay, CA ISBN 978-0-9791226-1-3
KATZ, P. Digital control using microprocessors. Englewood Cliffs: Prentice-Hall, 293p. 1981.
OGATA, K. Discrete-time control systems. Englewood Cliffs: Prentice-Hall,984p. 1987.
PHILLIPS, C.L.; NAGLE, H. T. Digital control system analysis and design. Englewood Cliffs, New Jersey: Prentice Hall International. 1995.
M. Sami Fadali, Antonio Visioli, (2009) "Digital Control Engineering", Academic Press, ISBN 978-0-12-374498-2.
JURY, E.I. Sampled-data control systems. New-York: John Wiley. 1958.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] "Referência Completa". mtc-m18.sid.inpe.br. Archived from the original on March 5, 2012.

[2] "Discrete attitude control of artificial satellites with flexible appendages" (PDF). mtc-m05.sid.inpe.br. Archived from the original (PDF) on 6 July 2011. Retrieved 12 January 2022.

[3] "An Analytical Approach for Discrete Controllers Design Using a New S-Z Mapping with Two Tuning Parameters". www.sae.org. Archived from the original on 13 January 2013. Retrieved 27 January 2022.

[4] Yamamoto, Yutaka (1996). "A Retrospective View on Sampled-Data - Control Systems" (PDF). Kyoto University . Archived from the original (PDF) on 22 July 2011. Retrieved 12 January 2022.

[5] Zavalishchin, S. T.; Sesekin, A. N. (28 February 1997). Dynamic Impulse Systems: Theory and Applications. Springer. ISBN 0792343948.

[6] "Author page". Association for Computing Machinery . Retrieved 2009-03-20.^{[ permanent dead link ‍]}

[:0-7] 1 2 Åström, Karl J.; Wittenmark, Björn (2013-06-13). Computer-Controlled Systems: Theory and Design, Third Edition. Courier Corporation. ISBN 978-0-486-28404-0.

[:1-8] 1 2 3 Short, Michael; Abugchem, Fathi; Abrar, Usama (2015-02-11). "Dependable Control for Wireless Distributed Control Systems". Electronics. 4 (4): 857–878. doi: 10.3390/electronics4040857 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]