Domain wall (magnetism)

Last updated

A domain wall is a term used in physics which can have similar meanings in magnetism, optics, or string theory. These phenomena can all be generically described as topological solitons which occur whenever a discrete symmetry is spontaneously broken. [1]

Contents

Magnetism

Domain wall (B) with gradual re-orientation of the magnetic moments between two 180-degree domains (A) and (C) (Presented is a Neel wall, and not a Bloch one, see below) Domain wall vectors.svg
Domain wall (B) with gradual re-orientation of the magnetic moments between two 180-degree domains (A) and (C)
(Presented is a Néel wall, and not a Bloch one, see below)

In magnetism, a domain wall is an interface separating magnetic domains. It is a transition between different magnetic moments and usually undergoes an angular displacement of 90° or 180°. A domain wall is a gradual reorientation of individual moments across a finite distance. The domain wall thickness depends on the anisotropy of the material, but on average spans across around 100–150 atoms.

The energy of a domain wall is simply the difference between the magnetic moments before and after the domain wall was created. This value is usually expressed as energy per unit wall area.

The width of the domain wall varies due to the two opposing energies that create it: the magnetocrystalline anisotropy energy and the exchange energy (), both of which tend to be as low as possible so as to be in a more favorable energetic state. The anisotropy energy is lowest when the individual magnetic moments are aligned with the crystal lattice axes thus reducing the width of the domain wall. Conversely, the exchange energy is reduced when the magnetic moments are aligned parallel to each other and thus makes the wall thicker, due to the repulsion between them (where anti-parallel alignment would bring them closer, working to reduce the wall thickness). In the end an equilibrium is reached between the two and the domain wall's width is set as such.

An ideal domain wall would be fully independent of position, but the structures are not ideal and so get stuck on inclusion sites within the medium, also known as crystallographic defects. These include missing or different (foreign) atoms, oxides, insulators and even stresses within the crystal. This prevents the formation of domain walls and also inhibits their propagation through the medium. Thus a greater applied magnetic field is required to overcome these sites.

Note that the magnetic domain walls are exact solutions to classical nonlinear equations of magnets (Landau–Lifshitz model, nonlinear Schrödinger equation and so on).

Symmetry of multiferroic domain walls

Since domain walls can be considered as thin layers, their symmetry is described by one of the 528 magnetic layer groups. [2] [3] To determine the layer's physical properties, a continuum approximation is used which leads to point-like layer groups. [4] If continuous translation operation is considering as identity, these groups transform to magnetic point groups. It was shown [5] that there are 125 such groups. It was found that if a magnetic point group is pyroelectric and/or pyromagnetic then the domain wall carries polarization and/or magnetization respectively. [6] These criteria were derived from the conditions of the appearance of the uniform polarization [7] [8] and/or magnetization. [9] [10] After their application to any inhomogeneous region, they predict the existence of even parts in functions of the distribution of order parameters. Identification of the remaining odd parts of these functions was formulated [11] based on symmetry transformations that interrelate domains. The symmetry classification of magnetic domain walls contains 64 magnetic point groups. [12]

Schematic representation of domain wall unpinning Barkhausensprung.gif
Schematic representation of domain wall unpinning

Symmetry-based predictions of the structure of the multiferroic domain walls have been proven using phenomenology coupling via magnetization [13] and/or polarization [14] spatial derivatives (flexomagnetoelectric). [15]

Depinning of a domain wall

Non-magnetic inclusions in the volume of a ferromagnetic material, or dislocations in crystallographic structure, can cause "pinning" of the domain walls (see animation). Such pinning sites cause the domain wall to sit in a local energy minimum and an external field is required to "unpin" the domain wall from its pinned position. The act of unpinning will cause sudden movement of the domain wall and sudden change of the volume of both neighbouring domains; this causes Barkhausen noise.

Types of walls

Bloch wall

A Bloch wall is a narrow transition region at the boundary between magnetic domains, over which the magnetization changes from its value in one domain to that in the next, named after the physicist Felix Bloch. In a Bloch domain wall, the magnetization rotates about the normal of the domain wall. In other words, the magnetization always points along the domain wall plane in a 3D system, in contrast to Néel domain walls.

Bloch domain walls appear in bulk materials, i.e. when sizes of magnetic material are considerably larger than domain wall width (according to the width definition of Lilley [16] ). In this case the energy of the demagnetization field does not impact the micromagnetic structure of the wall. Mixed cases are possible as well when the demagnetization field changes the magnetic domains (magnetization direction in domains) but not the domain walls. [17]

Néel wall

A Néel wall is a narrow transition region between magnetic domains, named after the French physicist Louis Néel. In the Néel wall, the magnetization smoothly rotates from the direction of magnetization within the first domain to the direction of magnetization within the second. In contrast to Bloch walls, the magnetization rotates about a line that is orthogonal to the normal of the domain wall. In other words, it rotates such that it points out of the domain wall plane in a 3D system. It consists of a core with fast varying rotation, where the magnetization points are nearly orthogonal to the two domains, and two tails where the rotation logarithmically decays. Néel walls are the common magnetic domain wall type in very thin films, where the exchange length is very large compared to the thickness. Without magnetic anisotropy Néel walls would spread across the whole volume.

See also

Related Research Articles

<span class="mw-page-title-main">Ferromagnetism</span> Mechanism by which materials form into and are attracted to magnets

Ferromagnetism is a property of certain materials that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagnetic materials are noticeably attracted to a magnet, which is a consequence of their substantial magnetic permeability.

<span class="mw-page-title-main">Antiferromagnetism</span> Regular pattern of magnetic moment ordering

In materials that exhibit antiferromagnetism, the magnetic moments of atoms or molecules, usually related to the spins of electrons, align in a regular pattern with neighboring spins pointing in opposite directions. This is, like ferromagnetism and ferrimagnetism, a manifestation of ordered magnetism. The phenomenon of antiferromagnetism was first introduced by Lev Landau in 1933.

Magnetostriction is a property of magnetic materials that causes them to change their shape or dimensions during the process of magnetization. The variation of materials' magnetization due to the applied magnetic field changes the magnetostrictive strain until reaching its saturation value, λ. The effect was first identified in 1842 by James Joule when observing a sample of iron.

Remanence or remanent magnetization or residual magnetism is the magnetization left behind in a ferromagnetic material after an external magnetic field is removed. Colloquially, when a magnet is "magnetized", it has remanence. The remanence of magnetic materials provides the magnetic memory in magnetic storage devices, and is used as a source of information on the past Earth's magnetic field in paleomagnetism. The word remanence is from remanent + -ence, meaning "that which remains". The origins of remanence originate from some point after 1850.

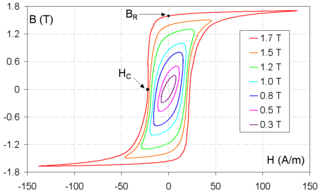
<span class="mw-page-title-main">Coercivity</span> Resistance of a ferromagnetic material to demagnetization by an external magnetic field

Coercivity, also called the magnetic coercivity, coercive field or coercive force, is a measure of the ability of a ferromagnetic material to withstand an external magnetic field without becoming demagnetized. Coercivity is usually measured in oersted or ampere/meter units and is denoted HC.

In physics, a ferromagnetic material is said to have magnetocrystalline anisotropy if it takes more energy to magnetize it in certain directions than in others. These directions are usually related to the principal axes of its crystal lattice. It is a special case of magnetic anisotropy. In other words, the excess energy required to magnetize a specimen in a particular direction over that required to magnetize it along the easy direction is called crystalline anisotropy energy.

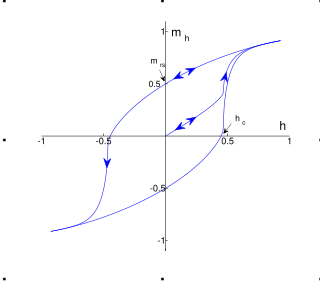
<span class="mw-page-title-main">Magnetic hysteresis</span> Application of an external magnetic field to a ferromagnet

Magnetic hysteresis occurs when an external magnetic field is applied to a ferromagnet such as iron and the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. This is the effect that provides the element of memory in a hard disk drive.

<span class="mw-page-title-main">Magnon</span> Spin 1 quasiparticle; quantum of a spin wave

A magnon is a quasiparticle, a collective excitation of the spin structure of an electron in a crystal lattice. In the equivalent wave picture of quantum mechanics, a magnon can be viewed as a quantized spin wave. Magnons carry a fixed amount of energy and lattice momentum, and are spin-1, indicating they obey boson behavior.

<span class="mw-page-title-main">Magnetization</span> Physical quantity, density of magnetic moment per volume

In classical electromagnetism, magnetization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material. Accordingly, physicists and engineers usually define magnetization as the quantity of magnetic moment per unit volume. It is represented by a pseudovector M. Magnetization can be compared to electric polarization, which is the measure of the corresponding response of a material to an electric field in electrostatics.

Multiferroics are defined as materials that exhibit more than one of the primary ferroic properties in the same phase:

Exchange bias or exchange anisotropy occurs in bilayers of magnetic materials where the hard magnetization behavior of an antiferromagnetic thin film causes a shift in the soft magnetization curve of a ferromagnetic film. The exchange bias phenomenon is of tremendous utility in magnetic recording, where it is used to pin the state of the readback heads of hard disk drives at exactly their point of maximum sensitivity; hence the term "bias."

Micromagnetics is a field of physics dealing with the prediction of magnetic behaviors at sub-micrometer length scales. The length scales considered are large enough for the atomic structure of the material to be ignored, yet small enough to resolve magnetic structures such as domain walls or vortices.

<span class="mw-page-title-main">Magnetic domain</span> Region of a magnetic material in which the magnetization has uniform direction

A magnetic domain is a region within a magnetic material in which the magnetization is in a uniform direction. This means that the individual magnetic moments of the atoms are aligned with one another and they point in the same direction. When cooled below a temperature called the Curie temperature, the magnetization of a piece of ferromagnetic material spontaneously divides into many small regions called magnetic domains. The magnetization within each domain points in a uniform direction, but the magnetization of different domains may point in different directions. Magnetic domain structure is responsible for the magnetic behavior of ferromagnetic materials like iron, nickel, cobalt and their alloys, and ferrimagnetic materials like ferrite. This includes the formation of permanent magnets and the attraction of ferromagnetic materials to a magnetic field. The regions separating magnetic domains are called domain walls, where the magnetization rotates coherently from the direction in one domain to that in the next domain. The study of magnetic domains is called micromagnetics.

In condensed matter physics, magnetic anisotropy describes how an object's magnetic properties can be different depending on direction. In the simplest case, there is no preferential direction for an object's magnetic moment. It will respond to an applied magnetic field in the same way, regardless of which direction the field is applied. This is known as magnetic isotropy. In contrast, magnetically anisotropic materials will be easier or harder to magnetize depending on which way the object is rotated.

<span class="mw-page-title-main">Magnetic structure</span> Ordered arrangement of magnetic spins in a material

The term magnetic structure of a material pertains to the ordered arrangement of magnetic spins, typically within an ordered crystallographic lattice. Its study is a branch of solid-state physics.

In physics, the Landau–Lifshitz–Gilbert equation, named for Lev Landau, Evgeny Lifshitz, and T. L. Gilbert, is a name used for a differential equation describing the dynamics of magnetization M in a solid. It is a modified version by Gilbert of the original equation of Landau and Lifshitz. The LLG equation is similar to the Bloch equation, but they differ in the form of the damping term. The LLG equation describes a more general scenario of magnetization dynamics beyond the simple Larmor precession. In particular, the effective field driving the precessional motion of M is not restricted to real magnetic fields; it incorporates a wide range of mechanisms including magnetic anisotropy, exchange interaction, and so on.

In its most general form, the magnetoelectric effect (ME) denotes any coupling between the magnetic and the electric properties of a material. The first example of such an effect was described by Wilhelm Röntgen in 1888, who found that a dielectric material moving through an electric field would become magnetized. A material where such a coupling is intrinsically present is called a magnetoelectric.

In magnetism, single domain refers to the state of a ferromagnet in which the magnetization does not vary across the magnet. A magnetic particle that stays in a single domain state for all magnetic fields is called a single domain particle. Such particles are very small. They are also very important in a lot of applications because they have a high coercivity. They are the main source of hardness in hard magnets, the carriers of magnetic storage in tape drives, and the best recorders of the ancient Earth's magnetic field.

<span class="mw-page-title-main">Demagnetizing field</span> Internal magnetic field generated by a magnet

The demagnetizing field, also called the stray field, is the magnetic field (H-field) generated by the magnetization in a magnet. The total magnetic field in a region containing magnets is the sum of the demagnetizing fields of the magnets and the magnetic field due to any free currents or displacement currents. The term demagnetizing field reflects its tendency to act on the magnetization so as to reduce the total magnetic moment. It gives rise to shape anisotropy in ferromagnets with a single magnetic domain and to magnetic domains in larger ferromagnets.

Néel relaxation theory is a theory developed by Louis Néel in 1949 to explain time-dependent magnetic phenomena known as magnetic viscosity. It is also called Néel-Arrhenius theory, after the Arrhenius equation, and Néel-Brown theory after a more rigorous derivation by William Fuller Brown, Jr. Néel used his theory to develop a model of thermoremanent magnetization in single-domain ferromagnetic minerals that explained how these minerals could reliably record the geomagnetic field. He also modeled frequency-dependent susceptibility and alternating field demagnetization.

References

  1. ↑ S. Weinberg, The Quantum Theory of Fields, Vol. 2. Chap 23, Cambridge University Press (1995).
  2. ↑ N. N. Neronova; N. V. Belov (1961). "Color antisymmetry mosaics". 6. Soviet Physics - Crystallography: 672–678.{{cite journal}}: Cite journal requires |journal= (help)
  3. ↑ Litvin, Daniel B. (1999). "Magnetic subperiodic groups". Acta Crystallographica Section A. 55 (5): 963–964. doi:10.1107/S0108767399003487. ISSN   0108-7673. PMID   10927306.
  4. ↑ Kopský, Vojtěch (1993). "Translation normalizers of Euclidean groups. I. Elementary theory". Journal of Mathematical Physics. 34 (4): 1548–1556. Bibcode:1993JMP....34.1548K. doi:10.1063/1.530173. ISSN   0022-2488.
  5. ↑ Přívratská, J.; Shaparenko, B.; Janovec, V.; Litvin, D. B. (2010). "Magnetic Point Group Symmetries of Spontaneously Polarized and/or Magnetized Domain Walls". Ferroelectrics. 269 (1): 39–44. doi:10.1080/713716033. ISSN   0015-0193. S2CID   202113942.
  6. ↑ Přívratská, J.; Janovec, V. (1999). "Spontaneous polarization and/or magnetization in non-ferroelastic domain walls: symmetry predictions". Ferroelectrics. 222 (1): 23–32. doi:10.1080/00150199908014794. ISSN   0015-0193.
  7. ↑ Walker, M. B.; Gooding, R. J. (1985). "Properties of Dauphiné-twin domain walls in quartz and berlinite". Physical Review B. 32 (11): 7408–7411. Bibcode:1985PhRvB..32.7408W. doi:10.1103/PhysRevB.32.7408. ISSN   0163-1829. PMID   9936884.
  8. ↑ P. Saint-Grkgoire and V. Janovec, in Lecture Notes on Physics 353, Nonlinear Coherent Structures, in: M. Barthes and J. LCon (Eds.), Springer-Verlag, Berlin, 1989, p. 117.
  9. ↑ L. Shuvalov, Sov. Phys. Crystallogr. 4 (1959) 399
  10. ↑ L. Shuvalov, Modern Crystallography IV : Physical Properties of Crystals, Springer, Berlin, 1988
  11. ↑ V.G. Bar'yakhtar; V. A. L'vov; D.A. Yablonskiy (1983). "Inhomogeneous magnetoelectric effect" (PDF). JETP Letters. 37 (12): 673–675. Archived from the original (PDF) on 2017-07-12. Retrieved 2019-04-14.
  12. ↑ Tanygin, B.M.; Tychko, O.V. (2009). "Magnetic symmetry of the plain domain walls in ferro- and ferrimagnets". Physica B: Condensed Matter. 404 (21): 4018–4022. arXiv: 1209.0003 . Bibcode:2009PhyB..404.4018T. doi:10.1016/j.physb.2009.07.150. ISSN   0921-4526. S2CID   118373839.
  13. ↑ Tanygin, B.M. (2011). "On the free energy of the flexomagnetoelectric interactions". Journal of Magnetism and Magnetic Materials. 323 (14): 1899–1902. arXiv: 1105.5300 . Bibcode:2011JMMM..323.1899T. doi:10.1016/j.jmmm.2011.02.035. ISSN   0304-8853. S2CID   119225609.
  14. ↑ Tanygin, B (2010). "Inhomogeneous Magnetoelectric Effect on Defect in Multiferroic Material: Symmetry Prediction". IOP Conference Series: Materials Science and Engineering. 15 (1): 012073. arXiv: 1007.3531 . Bibcode:2010MS&E...15a2073T. doi:10.1088/1757-899X/15/1/012073. ISSN   1757-899X. S2CID   119234063.
  15. ↑ Pyatakov, A. P.; Zvezdin, A. K. (2009). "Flexomagnetoelectric interaction in multiferroics". The European Physical Journal B. 71 (3): 419–427. Bibcode:2009EPJB...71..419P. doi:10.1140/epjb/e2009-00281-5. ISSN   1434-6028. S2CID   122234441.
  16. ↑ Lilley, B.A. (2010). "LXXI. Energies and widths of domain boundaries in ferromagnetics". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 41 (319): 792–813. doi:10.1080/14786445008561011. ISSN   1941-5982.
  17. ↑ D’yachenko, S. A.; Kovalenko, V. F.; Tanygin, B. N.; Tychko, A. V. (2011). "Influence of the demagnetizing field on the structure of a Bloch wall in a (001) plate of a magnetically ordered cubic crystal". Physics of the Solid State. 50 (1): 32–42. doi:10.1134/S1063783408010083. ISSN   1063-7834. S2CID   123608666.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.