In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of f and g. More precisely, if is the function such that for every x, then the chain rule is, in Lagrange's notation, or, equivalently,

In mathematics, convolution is a mathematical operation on two functions that produces a third function. The term convolution refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result. Graphically, it expresses how the 'shape' of one function is modified by the other.

In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function may be defined by:

In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.

In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.
Some Buddhist terms and concepts lack direct translations into English that cover the breadth of the original term. Below are given a number of important Buddhist terms, short definitions, and the languages in which they appear. In this list, an attempt has been made to organize terms by their original form and give translations and synonyms in other languages along with the definition.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed asWhere:
Time dilation is the difference in elapsed time as measured by two clocks, either because of a relative velocity between them, or a difference in gravitational potential between their locations. When unspecified, "time dilation" usually refers to the effect due to velocity.

Docodon is an extinct docodont mammaliaform from the Late Jurassic of western North America. It was the first docodont to be named.
Platypterygius is a historically paraphyletic genus of platypterygiine ichthyosaur from the Cretaceous period. It was historically used as a wastebasket taxon, and most species within Platypterygius likely are undiagnostic at the genus or species level, or represent distinct genera, even being argued as invalid. While fossils referred to Platypterygius have been found throughout different continents, the holotype specimen was found in Germany.

Cortinarius violaceus, commonly known as the violet webcap or violet cort, is a fungus in the webcap genus Cortinarius native across the Northern Hemisphere. The fruit bodies are dark purple mushrooms with caps up to 15 cm (6 in) across, sporting gills underneath. The stalk measures 6 to 12 centimetres by 1 to 2 cm, sometimes with a thicker base. The dark flesh has a smell reminiscent of cedar wood. Forming symbiotic (ectomycorrhizal) relationships with the roots of various plant species, C. violaceus is found predominantly in conifer forests in North America and deciduous forests in Europe.

Arthropterygius is a widespread genus of ophthalmosaurid ichthyosaur which existed in Canada, Norway, Russia, and Argentina from the late Jurassic period and possibly to the earliest Cretaceous.

Platypterygiinae is an extinct subfamily of ophthalmosaurid thunnosaur ichthyosaurs from the early Late Jurassic to the early Late Cretaceous of Asia, Australia, Europe, North America and South America. Currently, the oldest known platypterygiine is Brachypterygius. Platypterygiines were characterized by square tooth roots in cross-section, an extremely reduced extracondylar area of the basioccipital, prominent dorsal and ventral trochanters on humerus and ischiopubis lacking an obturator foramen.

Ophthalmosaurinae is an extinct subfamily of ophthalmosaurid thunnosaur ichthyosaurs from the Middle Jurassic to the late Early Cretaceous of Europe, North America and South America. Currently, the oldest and the basalmost, known ophthalmosaurine is Mollesaurus from the early Bajocian of Argentina. Ophthalmosaurines were characterized by a large extracondylar area of the basioccipital in the form of a thick and concave peripheral band, posterodistally deflected ulnar facet of the humerus, large ulna with concave and edgy posterior surface and ischiopubis with obturator foramen.

Sisteronia is an extinct genus of platypterygiine ophthalmosaurid ichthyosaur known from the 'middle' Cretaceous of southeastern England and southeastern France. It contains a single species, Sisteronia seeleyi.
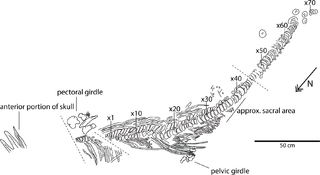
Keilhauia is a genus of ophthalmosaurid ichthyosaur, a type of dolphin-like, large-eyed marine reptile, from the Early Cretaceous shallow marine Slottsmøya Member of the Agardhfjellet Formation in Svalbard, Norway. The genus contains a single species, K. nui, known from a single specimen discovered in 2010 and described by Delsett et al. in 2017. In life, Keilhauia probably measured approximately 4 metres (13 ft) in length; it can be distinguished by other ophthalmosaurids by the wide top end of its ilium and the relatively short ischiopubis compared to the femur. Although it was placed in a basal position within the Ophthalmosauridae by phylogenetic analysis, this placement is probably incorrect.

Drepanocladus is a genus of mosses belonging to the family Amblystegiaceae. It has a cosmopolitan distribution












