Raoult's law ( law) is a relation of physical chemistry, with implications in thermodynamics. Proposed by French chemist François-Marie Raoult in 1887, it states that the partial pressure of each component of an ideal mixture of liquids is equal to the vapor pressure of the pure component multiplied by its mole fraction in the mixture. In consequence, the relative lowering of vapor pressure of a dilute solution of nonvolatile solute is equal to the mole fraction of solute in the solution.

Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of gravity (cg), known as pitch, roll and yaw. These are collectively known as aircraft attitude, often principally relative to the atmospheric frame in normal flight, but also relative to terrain during takeoff or landing, or when operating at low elevation. The concept of attitude is not specific to fixed-wing aircraft, but also extends to rotary aircraft such as helicopters, and dirigibles, where the flight dynamics involved in establishing and controlling attitude are entirely different.
In physical chemistry, Henry's law is a gas law that states that the amount of dissolved gas in a liquid is directly proportional at equilibrium to its partial pressure above the liquid. The proportionality factor is called Henry's law constant. It was formulated by the English chemist William Henry, who studied the topic in the early 19th century. In simple words, we can say that the partial pressure of a gas in vapour phase is directly proportional to the mole fraction of a gas in solution.

Flash evaporation is the partial vapor that occurs when a saturated liquid stream undergoes a reduction in pressure by passing through a throttling valve or other throttling device. This process is one of the simplest unit operations. If the throttling valve or device is located at the entry into a pressure vessel so that the flash evaporation occurs within the vessel, then the vessel is often referred to as a flash drum.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.

Dissociation in chemistry is a general process in which molecules (or ionic compounds such as salts, or complexes) separate or split into other things such as atoms, ions, or radicals, usually in a reversible manner. For instance, when an acid dissolves in water, a covalent bond between an electronegative atom and a hydrogen atom is broken by heterolytic fission, which gives a proton (H+) and a negative ion. Dissociation is the opposite of association or recombination.
In information theory, the Rényi entropy is a quantity that generalizes various notions of entropy, including Hartley entropy, Shannon entropy, collision entropy, and min-entropy. The Rényi entropy is named after Alfréd Rényi, who looked for the most general way to quantify information while preserving additivity for independent events. In the context of fractal dimension estimation, the Rényi entropy forms the basis of the concept of generalized dimensions.
In quantum mechanics, the Hellmann–Feynman theorem relates the derivative of the total energy with respect to a parameter to the expectation value of the derivative of the Hamiltonian with respect to that same parameter. According to the theorem, once the spatial distribution of the electrons has been determined by solving the Schrödinger equation, all the forces in the system can be calculated using classical electrostatics.
The Hückel method or Hückel molecular orbital theory, proposed by Erich Hückel in 1930, is a simple method for calculating molecular orbitals as linear combinations of atomic orbitals. The theory predicts the molecular orbitals for π-electrons in π-delocalized molecules, such as ethylene, benzene, butadiene, and pyridine. It provides the theoretical basis for Hückel's rule that cyclic, planar molecules or ions with π-electrons are aromatic. It was later extended to conjugated molecules such as pyridine, pyrrole and furan that contain atoms other than carbon and hydrogen (heteroatoms). A more dramatic extension of the method to include σ-electrons, known as the extended Hückel method (EHM), was developed by Roald Hoffmann. The extended Hückel method gives some degree of quantitative accuracy for organic molecules in general and was used to provide computational justification for the Woodward–Hoffmann rules. To distinguish the original approach from Hoffmann's extension, the Hückel method is also known as the simple Hückel method (SHM).
In mathematics, Fourier–Bessel series is a particular kind of generalized Fourier series based on Bessel functions.
The Gibbs adsorption isotherm for multicomponent systems is an equation used to relate the changes in concentration of a component in contact with a surface with changes in the surface tension, which results in a corresponding change in surface energy. For a binary system, the Gibbs adsorption equation in terms of surface excess is
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
A theoretical plate in many separation processes is a hypothetical zone or stage in which two phases, such as the liquid and vapor phases of a substance, establish an equilibrium with each other. Such equilibrium stages may also be referred to as an equilibrium stage, ideal stage, or a theoretical tray. The performance of many separation processes depends on having series of equilibrium stages and is enhanced by providing more such stages. In other words, having more theoretical plates increases the efficiency of the separation process be it either a distillation, absorption, chromatographic, adsorption or similar process.
In thermodynamics and chemical engineering, the vapor–liquid equilibrium (VLE) describes the distribution of a chemical species between the vapor phase and a liquid phase.
Relative volatility is a measure comparing the vapor pressures of the components in a liquid mixture of chemicals. This quantity is widely used in designing large industrial distillation processes. In effect, it indicates the ease or difficulty of using distillation to separate the more volatile components from the less volatile components in a mixture. By convention, relative volatility is usually denoted as .

The Fréchet distribution, also known as inverse Weibull distribution, is a special case of the generalized extreme value distribution. It has the cumulative distribution function
In the following we solve the second-order differential equation called the hypergeometric differential equation using Frobenius method, named after Ferdinand Georg Frobenius. This is a method that uses the series solution for a differential equation, where we assume the solution takes the form of a series. This is usually the method we use for complicated ordinary differential equations.
In mathematics, Katugampola fractional operators are integral operators that generalize the Riemann–Liouville and the Hadamard fractional operators into a unique form. The Katugampola fractional integral generalizes both the Riemann–Liouville fractional integral and the Hadamard fractional integral into a single form and It is also closely related to the Erdelyi–Kober operator that generalizes the Riemann–Liouville fractional integral. Katugampola fractional derivative has been defined using the Katugampola fractional integral and as with any other fractional differential operator, it also extends the possibility of taking real number powers or complex number powers of the integral and differential operators.
Aspen Plus, Aspen HYSYS, ChemCad and MATLAB, PRO are the commonly used process simulators for modeling, simulation and optimization of a distillation process in the chemical industries. Distillation is the technique of preferential separation of the more volatile components from the less volatile ones in a feed followed by condensation. The vapor produced is richer in the more volatile components. The distribution of the component in the two phase is governed by the vapour-liquid equilibrium relationship. In practice, distillation may be carried out by either two principal methods. The first method is based on the production of vapor boiling the liquid mixture to be separated and condensing the vapors without allowing any liquid to return to the still. There is no reflux. The second method is based on the return of part of the condensate to still under such conditions that this returning liquid is brought into intimate contact with the vapors on their way to condenser.
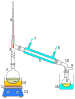
Distillation is a process in which we separate components of different vapour pressure. One fraction leaves overhead and is condensed to distillate and the other is the bottom product. The bottom product is mostly liquid while the overhead fraction can be vapour or an aerosol. This method requires the components to have different volatility to be separated.