
The characteristic impedance or surge impedance (usually written Z0) of a uniform transmission line is the ratio of the amplitudes of voltage and current of a wave travelling in one direction along the line in the absence of reflections in the other direction. Equivalently, it can be defined as the input impedance of a transmission line when its length is infinite. Characteristic impedance is determined by the geometry and materials of the transmission line and, for a uniform line, is not dependent on its length. The SI unit of characteristic impedance is the ohm.

In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmission must be taken into account. This applies especially to radio-frequency engineering because the short wavelengths mean that wave phenomena arise over very short distances. However, the theory of transmission lines was historically developed to explain phenomena on very long telegraph lines, especially submarine telegraph cables.

In electrical engineering, impedance is the opposition to alternating current presented by the combined effect of resistance and reactance in a circuit.
In electrical circuits, reactance is the opposition presented to alternating current by inductance and capacitance. Along with resistance, it is one of two elements of impedance; however, while both elements involve transfer of electrical energy, no dissipation of electrical energy as heat occurs in reactance; instead, the reactance stores energy until a quarter-cycle later when the energy is returned to the circuit. Greater reactance gives smaller current for the same applied voltage.
In electrical engineering, admittance is a measure of how easily a circuit or device will allow a current to flow. It is defined as the reciprocal of impedance, analogous to how conductance and resistance are defined. The SI unit of admittance is the siemens ; the older, synonymous unit is mho, and its symbol is ℧. Oliver Heaviside coined the term admittance in December 1887. Heaviside used Y to represent the magnitude of admittance, but it quickly became the conventional symbol for admittance itself through the publications of Charles Proteus Steinmetz. Heaviside probably chose Y simply because it is next to Z in the alphabet, the conventional symbol for impedance.
In electronics, a voltage divider (also known as a potential divider) is a passive linear circuit that produces an output voltage (Vout) that is a fraction of its input voltage (Vin). Voltage division is the result of distributing the input voltage among the components of the divider. A simple example of a voltage divider is two resistors connected in series, with the input voltage applied across the resistor pair and the output voltage emerging from the connection between them.

A gyrator is a passive, linear, lossless, two-port electrical network element proposed in 1948 by Bernard D. H. Tellegen as a hypothetical fifth linear element after the resistor, capacitor, inductor and ideal transformer. Unlike the four conventional elements, the gyrator is non-reciprocal. Gyrators permit network realizations of two-(or-more)-port devices which cannot be realized with just the four conventional elements. In particular, gyrators make possible network realizations of isolators and circulators. Gyrators do not however change the range of one-port devices that can be realized. Although the gyrator was conceived as a fifth linear element, its adoption makes both the ideal transformer and either the capacitor or inductor redundant. Thus the number of necessary linear elements is in fact reduced to three. Circuits that function as gyrators can be built with transistors and op-amps using feedback.

The Butterworth filter is a type of signal processing filter designed to have a frequency response that is as flat as possible in the passband. It is also referred to as a maximally flat magnitude filter. It was first described in 1930 by the British engineer and physicist Stephen Butterworth in his paper entitled "On the Theory of Filter Amplifiers".
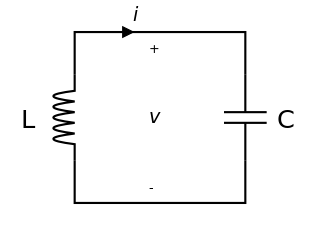
An LC circuit, also called a resonant circuit, tank circuit, or tuned circuit, is an electric circuit consisting of an inductor, represented by the letter L, and a capacitor, represented by the letter C, connected together. The circuit can act as an electrical resonator, an electrical analogue of a tuning fork, storing energy oscillating at the circuit's resonant frequency.

In microwave and radio-frequency engineering, a stub or resonant stub is a length of transmission line or waveguide that is connected at one end only. The free end of the stub is either left open-circuit, or short-circuited. Neglecting transmission line losses, the input impedance of the stub is purely reactive; either capacitive or inductive, depending on the electrical length of the stub, and on whether it is open or short circuit. Stubs may thus function as capacitors, inductors and resonant circuits at radio frequencies.

Electrical resonance occurs in an electric circuit at a particular resonant frequency when the impedances or admittances of circuit elements cancel each other. In some circuits, this happens when the impedance between the input and output of the circuit is almost zero and the transfer function is close to one.
Electronic filter topology defines electronic filter circuits without taking note of the values of the components used but only the manner in which those components are connected.

Zobel networks are a type of filter section based on the image-impedance design principle. They are named after Otto Zobel of Bell Labs, who published a much-referenced paper on image filters in 1923. The distinguishing feature of Zobel networks is that the input impedance is fixed in the design independently of the transfer function. This characteristic is achieved at the expense of a much higher component count compared to other types of filter sections. The impedance would normally be specified to be constant and purely resistive. For this reason, Zobel networks are also known as constant resistance networks. However, any impedance achievable with discrete components is possible.

Prototype filters are electronic filter designs that are used as a template to produce a modified filter design for a particular application. They are an example of a nondimensionalised design from which the desired filter can be scaled or transformed. They are most often seen in regard to electronic filters and especially linear analogue passive filters. However, in principle, the method can be applied to any kind of linear filter or signal processing, including mechanical, acoustic and optical filters.
Positive-real functions, often abbreviated to PR function or PRF, are a kind of mathematical function that first arose in electrical network synthesis. They are complex functions, Z(s), of a complex variable, s. A rational function is defined to have the PR property if it has a positive real part and is analytic in the right half of the complex plane and takes on real values on the real axis.

The primary line constants are parameters that describe the characteristics of conductive transmission lines, such as pairs of copper wires, in terms of the physical electrical properties of the line. The primary line constants are only relevant to transmission lines and are to be contrasted with the secondary line constants, which can be derived from them, and are more generally applicable. The secondary line constants can be used, for instance, to compare the characteristics of a waveguide to a copper line, whereas the primary constants have no meaning for a waveguide.

An RLC circuit is an electrical circuit consisting of a resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the constituent components of this circuit, where the sequence of the components may vary from RLC.
Belevitch's theorem is a theorem in electrical network analysis due to the Russo-Belgian mathematician Vitold Belevitch (1921–1999). The theorem provides a test for a given S-matrix to determine whether or not it can be constructed as a lossless rational two-port network.
Network synthesis is a design technique for linear electrical circuits. Synthesis starts from a prescribed impedance function of frequency or frequency response and then determines the possible networks that will produce the required response. The technique is to be compared to network analysis in which the response of a given circuit is calculated. Prior to network synthesis, only network analysis was available, but this requires that one already knows what form of circuit is to be analysed. There is no guarantee that the chosen circuit will be the closest possible match to the desired response, nor that the circuit is the simplest possible. Network synthesis directly addresses both these issues. Network synthesis has historically been concerned with synthesising passive networks, but is not limited to such circuits.
Richards' theorem is a mathematical result due to Paul I. Richards in 1947. The theorem states that for,




















![Foster's first form of canonical driving point impedance realisation. If the polynomial function has a pole at o=0 one of the LC sections will reduce to a single capacitor. If the polynomial function has a pole at o=[?] one of the LC sections will reduce to a single inductor. If both poles are present then two sections reduce to a series LC circuit. Foster driving point 1st kind.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/5/50/Foster_driving_point_1st_kind.svg/220px-Foster_driving_point_1st_kind.svg.png)
![Foster's second form of canonical driving point impedance realisation. If the polynomial function has a zero at o=0 one of the LC sections will reduce to a single inductor. If the polynomial function has a zero at o=[?] one of the LC sections will reduce to a single capacitor. If both zeroes are present then two sections reduce to a parallel LC circuit. Foster driving point 2nd kind.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/b/b8/Foster_driving_point_2nd_kind.svg/220px-Foster_driving_point_2nd_kind.svg.png)
















