
The decimal numeral system is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as decimal notation.
The duodecimal system, also known as base twelve or dozenal, is a positional numeral system using twelve as its base. In duodecimal, the number twelve is denoted "10", meaning 1 twelve and 0 units; in the decimal system, this number is instead written as "12" meaning 1 ten and 2 units, and the string "10" means ten. In duodecimal, "100" means twelve squared, "1000" means twelve cubed, and "0.1" means a twelfth.

Erlang is a general-purpose, concurrent, functional high-level programming language, and a garbage-collected runtime system. The term Erlang is used interchangeably with Erlang/OTP, or Open Telecom Platform (OTP), which consists of the Erlang runtime system, several ready-to-use components (OTP) mainly written in Erlang, and a set of design principles for Erlang programs.
Specific impulse is a measure of how efficiently a reaction mass engine, such as a rocket using propellant or a jet engine using fuel, generates thrust.
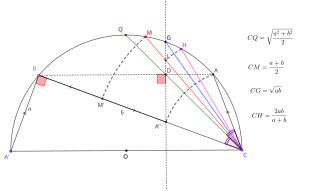
In ordinary language, an average is a single number or value that best represents a set of data. The type of average taken as most typically representative of a list of numbers is the arithmetic mean – the sum of the numbers divided by how many numbers are in the list. For example, the mean average of the numbers 2, 3, 4, 7, and 9 is 5. Depending on the context, the most representative statistic to be taken as the average might be another measure of central tendency, such as the mid-range, median, mode or geometric mean. For example, the average personal income is often given as the median – the number below which are 50% of personal incomes and above which are 50% of personal incomes – because the mean would be higher by including personal incomes from a few billionaires. For this reason, it is recommended to avoid using the word "average" when discussing measures of central tendency and specify which average measure is being used.

Professor John I.Q. Nerdelbaum Frink Jr. is a recurring character in the animated television series The Simpsons. He is voiced by Hank Azaria, and first appeared in the 1991 episode "Old Money". Frink is Springfield's nerdy scientist and professor and is extremely intelligent, though somewhat mad and socially inept. Frink often tries to use his bizarre inventions to aid the town in its crises but they usually only make things worse. His manner of speech, including the impulsive shouting of nonsensical words, has become his trademark.

A vernier scalever-NEE-er), named after Pierre Vernier, is a visual aid to take an accurate measurement reading between two graduation markings on a linear scale by using mechanical interpolation, thereby increasing resolution and reducing measurement uncertainty by using vernier acuity to reduce human estimation error. It may be found on many types of instrument measuring linear or angular quantities, but in particular on a vernier caliper, which measures lengths.
In cryptography, coincidence counting is the technique of putting two texts side-by-side and counting the number of times that identical letters appear in the same position in both texts. This count, either as a ratio of the total or normalized by dividing by the expected count for a random source model, is known as the index of coincidence, or IC for short.
In computing, online analytical processing, or OLAP, is an approach to quickly answer multi-dimensional analytical (MDA) queries. The term OLAP was created as a slight modification of the traditional database term online transaction processing (OLTP). OLAP is part of the broader category of business intelligence, which also encompasses relational databases, report writing and data mining. Typical applications of OLAP include business reporting for sales, marketing, management reporting, business process management (BPM), budgeting and forecasting, financial reporting and similar areas, with new applications emerging, such as agriculture.
An off-by-one error or off-by-one bug is a logic error that involves a number that differs from its intended value by +1 or −1. An off-by-one error can sometimes appear in a mathematical context. It often occurs in computer programming when a loop iterates one time too many or too few, usually caused by the use of non-strict inequality (≤) as the terminating condition where strict inequality (<) should have been used, or vice versa. Off-by-one errors also stem from confusion over zero-based numbering.

Counting is the process of determining the number of elements of a finite set of objects; that is, determining the size of a set. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once, until no unmarked elements are left; if the counter was set to one after the first object, the value after visiting the final object gives the desired number of elements. The related term enumeration refers to uniquely identifying the elements of a finite (combinatorial) set or infinite set by assigning a number to each element.
A numerical digit or numeral is a single symbol used alone or in combinations, to represent numbers in a positional numeral system. The name "digit" comes from the fact that the ten digits of the hands correspond to the ten symbols of the common base 10 numeral system, i.e. the decimal digits.
Readability is the ease with which a reader can understand a written text. The concept exists in both natural language and programming languages though in different forms. In natural language, the readability of text depends on its content and its presentation. In programming, things such as programmer comments, choice of loop structure, and choice of names can determine the ease with which humans can read computer program code.
A Fermi problem, also known as an order-of-magnitude problem, is an estimation problem in physics or engineering education, designed to teach dimensional analysis or approximation of extreme scientific calculations. Fermi problems are usually back-of-the-envelope calculations. The estimation technique is named after physicist Enrico Fermi as he was known for his ability to make good approximate calculations with little or no actual data. Fermi problems typically involve making justified guesses about quantities and their variance or lower and upper bounds. In some cases, order-of-magnitude estimates can also be derived using dimensional analysis.
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science. The computability of a problem is closely linked to the existence of an algorithm to solve the problem.

Mental calculation consists of arithmetical calculations using only the human brain, with no help from any supplies or devices such as a calculator. People may use mental calculation when computing tools are not available, when it is faster than other means of calculation, or even in a competitive context. Mental calculation often involves the use of specific techniques devised for specific types of problems. People with unusually high ability to perform mental calculations are called mental calculators or lightning calculators.
The Trachtenberg system is a system of rapid mental calculation. The system consists of a number of readily memorized operations that allow one to perform arithmetic computations very quickly. It was developed by the Ukrainian engineer Jakow Trachtenberg in order to keep his mind occupied while being in a Nazi concentration camp.
Windows Calculator is a software calculator developed by Microsoft and included in Windows. In its Windows 10 incarnation it has four modes: standard, scientific, programmer, and a graphing mode. The standard mode includes a number pad and buttons for performing arithmetic operations. The scientific mode takes this a step further and adds exponents and trigonometric function, and programmer mode allows the user to perform operations related to computer programming. In 2020, a graphing mode was added to the Calculator, allowing users to graph equations on a coordinate plane.
Ancient Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt c. 3000 to c. 300 BCE, from the Old Kingdom of Egypt until roughly the beginning of Hellenistic Egypt. The ancient Egyptians utilized a numeral system for counting and solving written mathematical problems, often involving multiplication and fractions. Evidence for Egyptian mathematics is limited to a scarce amount of surviving sources written on papyrus. From these texts it is known that ancient Egyptians understood concepts of geometry, such as determining the surface area and volume of three-dimensional shapes useful for architectural engineering, and algebra, such as the false position method and quadratic equations.

Contribution margin (CM), or dollar contribution per unit, is the selling price per unit minus the variable cost per unit. "Contribution" represents the portion of sales revenue that is not consumed by variable costs and so contributes to the coverage of fixed costs. This concept is one of the key building blocks of break-even analysis.








