Related Research Articles
In astronomy, declination is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. Declination's angle is measured north or south of the celestial equator, along the hour circle passing through the point in question.
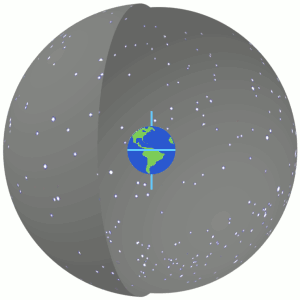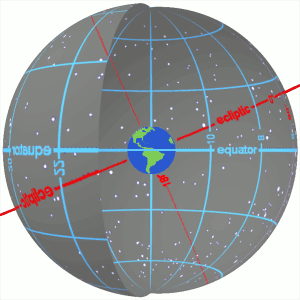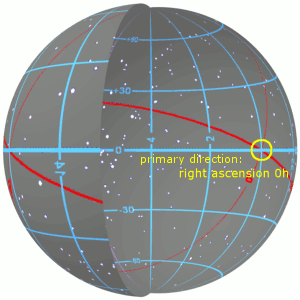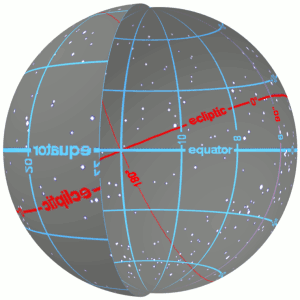
The ecliptic or ecliptic plane is the orbital plane of Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the background of stars. The ecliptic is an important reference plane and is the basis of the ecliptic coordinate system.
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.
Right ascension is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the point in question above the earth. When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system.
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, which may be centered on Earth or the observer. If centered on the observer, half of the sphere would resemble a hemispherical screen over the observing location.
Astronomical coordinate systems are organized arrangements for specifying positions of satellites, planets, stars, galaxies, and other celestial objects relative to physical reference points available to a situated observer. Coordinate systems in astronomy can specify an object's position in three-dimensional space or plot merely its direction on a celestial sphere, if the object's distance is unknown or trivial.
The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere, a primary direction towards the vernal equinox, and a right-handed convention.
The ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. Because most planets and many small Solar System bodies have orbits with only slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the vernal (March) equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates.
The galactic coordinate system is a celestial coordinate system in spherical coordinates, with the Sun as its center, the primary direction aligned with the approximate center of the Milky Way Galaxy, and the fundamental plane parallel to an approximation of the galactic plane but offset to its north. It uses the right-handed convention, meaning that coordinates are positive toward the north and toward the east in the fundamental plane.
In astronomy, an epoch or reference epoch is a moment in time used as a reference point for some time-varying astronomical quantity. It is useful for the celestial coordinates or orbital elements of a celestial body, as they are subject to perturbations and vary with time. These time-varying astronomical quantities might include, for example, the mean longitude or mean anomaly of a body, the node of its orbit relative to a reference plane, the direction of the apogee or aphelion of its orbit, or the size of the major axis of its orbit.
Spherical astronomy, or positional astronomy, is a branch of observational astronomy used to locate astronomical objects on the celestial sphere, as seen at a particular date, time, and location on Earth. It relies on the mathematical methods of spherical geometry and the measurements of astrometry.
The orbital plane of a revolving body is the geometric plane in which its orbit lies. Three non-collinear points in space suffice to determine an orbital plane. A common example would be the positions of the centers of a massive body (host) and of an orbiting celestial body at two different times/points of its orbit.
An orbital pole is either point at the ends of an imaginary line segment that runs through the center of an orbit and is perpendicular to the orbital plane. Projected onto the celestial sphere, orbital poles are similar in concept to celestial poles, but are based on the body's orbit instead of its equator.
The navigational triangle or PZX triangle is a spherical triangle used in astronavigation to determine the observer's position on the globe. It is composed of three reference points on the celestial sphere:
The Earth-centered, Earth-fixed coordinate system, also known as the geocentric coordinate system, is a cartesian spatial reference system that represents locations in the vicinity of the Earth as X, Y, and Z measurements from its center of mass. Its most common use is in tracking the orbits of satellites and in satellite navigation systems for measuring locations on the surface of the Earth, but it is also used in applications such as tracking crustal motion.
The poles of astronomical bodies are determined based on their axis of rotation in relation to the celestial poles of the celestial sphere. Astronomical bodies include stars, planets, dwarf planets and small Solar System bodies such as comets and minor planets, as well as natural satellites and minor-planet moons.
In astronomy, an equinox is either of two places on the celestial sphere at which the ecliptic intersects the celestial equator. Although there are two such intersections, the equinox associated with the Sun's ascending node is used as the conventional origin of celestial coordinate systems and referred to simply as "the equinox". In contrast to the common usage of spring/vernal and autumnal equinoxes, the celestial coordinate system equinox is a direction in space rather than a moment in time.
Earth-centered inertial (ECI) coordinate frames have their origins at the center of mass of Earth and are fixed with respect to the star. "I" in "ECI" stands for inertial, in contrast to the "Earth-centered - Earth-fixed" (ECEF) frames, which remains fixed with respect to Earth's surface in its rotation, and then rotates with respect to stars.
This glossary of astronomy is a list of definitions of terms and concepts relevant to astronomy and cosmology, their sub-disciplines, and related fields. Astronomy is concerned with the study of celestial objects and phenomena that originate outside the atmosphere of Earth. The field of astronomy features an extensive vocabulary and a significant amount of jargon.
A planetary coordinate system is a generalization of the geographic coordinate system and the geocentric coordinate system for planets other than Earth. Similar coordinate systems are defined for other solid celestial bodies, such as in the selenographic coordinates for the Moon. The coordinate systems for almost all of the solid bodies in the Solar System were established by Merton E. Davies of the Rand Corporation, including Mercury, Venus, Mars, the four Galilean moons of Jupiter, and Triton, the largest moon of Neptune.
References
- ↑ Rogers, Lucy (2008), It's ONLY Rocket Science: An Introduction in Plain English, Springer, p. 136, ISBN 9780387753782 .
- ↑ Newcomb, Simon (1906). A Compendium of Spherical Astronomy with Its Applications to the Determination and Reduction of Positions of the Fixed Stars. Macmillan. p. 92..
- ↑ "NASA - Besselian Elements of Solar Eclipses". NASA. Retrieved 13 August 2022.
 | This elementary geometry-related article is a stub. You can help Wikipedia by expanding it. |