
The Galilean moons, or Galilean satellites, are the four largest moons of Jupiter: Io, Europa, Ganymede, and Callisto. They are the most readily visible Solar System objects after Saturn, the dimmest of the classical planets; though their closeness to bright Jupiter makes naked-eye observation very difficult, they are readily seen with common binoculars, even under night sky conditions of high light pollution. The invention of the telescope enabled the discovery of the moons in 1610. Through this, they became the first Solar System objects discovered since humans have started tracking the classical planets, and the first objects to be found to orbit any planet beyond Earth.
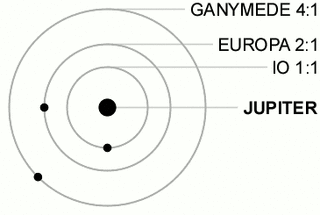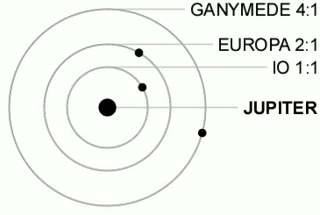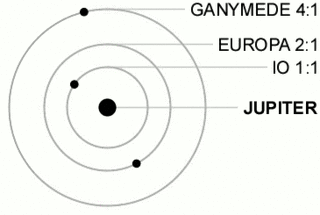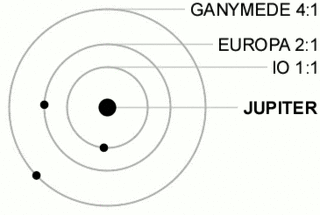
In celestial mechanics, orbital resonance occurs when orbiting bodies exert regular, periodic gravitational influence on each other, usually because their orbital periods are related by a ratio of small integers. Most commonly, this relationship is found between a pair of objects. The physical principle behind orbital resonance is similar in concept to pushing a child on a swing, whereby the orbit and the swing both have a natural frequency, and the body doing the "pushing" will act in periodic repetition to have a cumulative effect on the motion. Orbital resonances greatly enhance the mutual gravitational influence of the bodies. In most cases, this results in an unstable interaction, in which the bodies exchange momentum and shift orbits until the resonance no longer exists. Under some circumstances, a resonant system can be self-correcting and thus stable. Examples are the 1:2:4 resonance of Jupiter's moons Ganymede, Europa and Io, and the 2:3 resonance between Neptune and Pluto. Unstable resonances with Saturn's inner moons give rise to gaps in the rings of Saturn. The special case of 1:1 resonance between bodies with similar orbital radii causes large planetary system bodies to eject most other bodies sharing their orbits; this is part of the much more extensive process of clearing the neighbourhood, an effect that is used in the current definition of a planet.

In astronomy, a conjunction occurs when two astronomical objects or spacecraft appear to be close to each other in the sky. This means they have either the same right ascension or the same ecliptic longitude, usually as observed from Earth.

An apsis is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides is the line connecting the two extreme values.

In the Hipparchian, Ptolemaic, and Copernican systems of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets. In particular it explained the apparent retrograde motion of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from the Earth.

In astronomy, a planet's elongation is the angular separation between the Sun and the planet, with Earth as the reference point.

In astrology, an aspect is an angle that planets make to each other in the horoscope; as well as to the Ascendant, Midheaven, Descendant, Lower Midheaven, and other points of astrological interest. As viewed from Earth, aspects are measured by the angular distance in degrees and minutes of ecliptic longitude between two points. According to astrological tradition, they indicate the timing of transitions and developmental changes in the lives of people and affairs relative to the Earth.

In astronomy, a transit is the passage of a celestial body directly between a larger body and the observer. As viewed from a particular vantage point, the transiting body appears to move across the face of the larger body, covering a small portion of it.
A classical planet is an astronomical object that is visible to the naked eye and moves across the sky and its backdrop of fixed stars. Visible to humans on Earth there are seven classical planets. They are from brightest to dimmest: the Sun, the Moon, Venus, Jupiter, Mars, Mercury and Saturn.

In astronomy, an extraterrestrial sky is a view of outer space from the surface of an astronomical body other than Earth.
A triple conjunction is an astronomical event when two planets or a planet and a star appear to meet each other three times during a brief period, either in opposition or at the time of inferior conjunction, if an inferior planet is involved. The visible movement of the planet or the planets in the sky appears therefore normally prograde at the first conjunction, retrograde at the second conjunction, and again prograde at the third conjunction.

Many astronomical phenomena viewed from the planet Mars are the same as or similar to those seen from Earth; but some are quite different. For example, because the atmosphere of Mars does not contain an ozone layer, it is also possible to make UV observations from the surface of Mars.

Solar eclipses on Jupiter occur when any of the natural satellites of Jupiter pass in front of the Sun as seen from the planet Jupiter.

Appulse is the least apparent distance between one celestial object and another, as seen from a third body during a given period. Appulse is seen in the apparent motion typical of two planets together in the sky, or of the Moon to a star or planet while the Moon orbits Earth, as seen from Earth. An appulse is an apparent phenomenon caused by perspective only; the two objects involved are not near in physical space.

Paul Wittich was a German mathematician and astronomer whose Capellan geoheliocentric model, in which the inner planets Mercury and Venus orbit the Sun but the outer planets Mars, Jupiter and Saturn orbit the Earth, may have directly inspired Tycho Brahe's more radically heliocentric geoheliocentric model in which all the 5 known primary planets orbited the Sun, which in turn orbited the stationary Earth.

Discovery and exploration of the Solar System is observation, visitation, and increase in knowledge and understanding of Earth's "cosmic neighborhood". This includes the Sun, Earth and the Moon, the major planets Mercury, Venus, Mars, Jupiter, Saturn, Uranus, and Neptune, their satellites, as well as smaller bodies including comets, asteroids, and dust.

Solar eclipses on Saturn occur when the natural satellites of Saturn pass in front of the Sun as seen from Saturn. These eclipses happen fairly often. For example, some of Saturn's moons can have a solar eclipse every day depending on the saturnian season.

In positional astronomy, two astronomical objects are said to be in opposition when they are on opposite sides of the celestial sphere, as observed from a given body.

Venus has an orbit with a semi-major axis of 0.723 au, and an eccentricity of 0.007. The low eccentricity and comparatively small size of its orbit give Venus the least range in distance between perihelion and aphelion of the planets: 1.46 million km. The planet orbits the Sun once every 225 days and travels 4.54 au in doing so, giving an average orbital speed of 35 km/s (78,000 mph).

The Kirkhill Astronomical Pillar was constructed in 1776 by David Stewart Erskine, 11th Earl of Buchan and erected in the grounds of his estate at Kirkhill House, near Broxburn, Scotland. The pillar fell into disrepair and eventually collapsed in the 1970s but fortunately the stones were preserved and the pillar was reconstructed (1988) in Almondell Country Park on land once owned by the Erskine family. The pillar records the details of an adjacent scale model of the Solar System constructed by Erskine following the measurements of the size of the Solar System deduced from the observations of the Transits of Venus in 1761 and 1769. The model, centred on a Sun of stone six feet in diameter with planets at distances and sizes to scale, has long since disappeared; only the pillar remains.
































