Hankinson's equation

Last updated

Hankinson's equation (also called Hankinson's formula or Hankinson's criterion) [1] is a mathematical relationship for predicting the off-axis uniaxial compressive strength of wood. The formula can also be used to compute the fiber stress or the stress wave velocity at the elastic limit as a function of grain angle in wood. For a wood that has uniaxial compressive strengths of parallel to the grain and perpendicular to the grain, Hankinson's equation predicts that the uniaxial compressive strength of the wood in a direction at an angle to the grain is given by

Wood grain

Wood grain is the longitudinal arrangement of wood fibers or the pattern resulting from this.

Contents

Even though the original relation was based on studies of spruce, Hankinson's equation has been found to be remarkably accurate for many other types of wood. A generalized form of the Hankinson formula has also been used for predicting the uniaxial tensile strength of wood at an angle to the grain. This formula has the form [2]

Spruce genus of plants

A spruce is a tree of the genus Picea, a genus of about 35 species of coniferous evergreen trees in the family Pinaceae, found in the northern temperate and boreal (taiga) regions of the Earth. Spruces are large trees, from about 20–60 m tall when mature, and have whorled branches and conical form. They can be distinguished from other members of the pine family by their needles (leaves), which are four-sided and attached singly to small persistent peg-like structures on the branches, and by their cones, which hang downwards after they are pollinated. The needles are shed when 4–10 years old, leaving the branches rough with the retained pegs. In other similar genera, the branches are fairly smooth.

where the exponent can take values between 1.5 and 2.

The stress wave velocity at angle to the grain at the elastic limit can similarly be obtained from the Hankinson formula

where is the velocity parallel to the grain, is the velocity perpendicular to the grain and is the grain angle.

See also

Failure theory is the science of predicting the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure (fracture) or ductile failure (yield). Depending on the conditions most materials can fail in a brittle or ductile manner or both. However, for most practical situations, a material may be classified as either brittle or ductile. Though failure theory has been in development for over 200 years, its level of acceptability is yet to reach that of continuum mechanics.

Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of continuum mechanics. The fundamental "linearizing" assumptions of linear elasticity are: infinitesimal strains or "small" deformations and linear relationships between the components of stress and strain. In addition linear elasticity is valid only for stress states that do not produce yielding. These assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis.

Hookes law principle of physics that states that the force (F) needed to extend or compress a spring by some distance X scales linearly with respect to that distance

Hooke's law is a law of physics that states that the force needed to extend or compress a spring by some distance x scales linearly with respect to that distance. That is: , where k is a constant factor characteristic of the spring: its stiffness, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law already in 1660.

Related Research Articles

Pauli matrices Matrices important in quantum mechanics and the study of spin

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries. They are

Rutherford scattering

Rutherford scattering is the elastic scattering of charged particles by the Coulomb interaction. It is a physical phenomenon explained by Ernest Rutherford in 1911 that led to the development of the planetary Rutherford model of the atom and eventually the Bohr model. Rutherford scattering was first referred to as Coulomb scattering because it relies only upon the static electric (Coulomb) potential, and the minimum distance between particles is set entirely by this potential. The classical Rutherford scattering process of alpha particles against gold nuclei is an example of "elastic scattering" because neither the alpha particles nor the gold nuclei are internally excited. The Rutherford formula further neglects the recoil kinetic energy of the massive target nucleus.

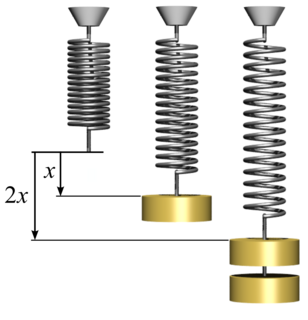
In science, buckling is a mathematical instability that leads to a failure mode.

Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope. Generally the theory applies to materials for which the compressive strength far exceeds the tensile strength.

Bending stress made by bending moment

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.

Etendue or étendue is a property of light in an optical system, which characterizes how "spread out" the light is in area and angle. It corresponds to the beam parameter product (BPP) in Gaussian optics.

Great-circle navigation

Great-circle navigation or orthodromic navigation is the practice of navigating a vessel along a great circle. Such routes yield the shortest distance between two points on the globe.

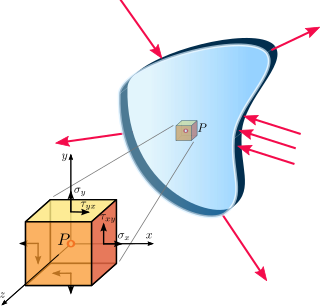
Plane stress

In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2. A related notion, plane strain, is often applicable to very thick members.

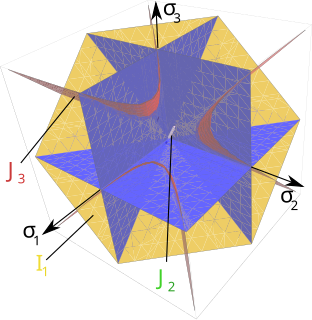
Yield surface

A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the material is said to have become plastic. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size of the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity, though not in some models of viscoplasticity.

Drucker–Prager yield criterion

The Drucker–Prager yield criterion is a pressure-dependent model for determining whether a material has failed or undergone plastic yielding. The criterion was introduced to deal with the plastic deformation of soils. It and its many variants have been applied to rock, concrete, polymers, foams, and other pressure-dependent materials.

Willam-Warnke yield criterion

The Willam-Warnke yield criterion is a function that is used to predict when failure will occur in concrete and other cohesive-frictional materials such as rock, soil, and ceramics. This yield criterion has the functional form

Flamant solution

The Flamant solution provides expressions for the stresses and displacements in a linear elastic wedge loaded by point forces at its sharp end. This solution was developed by A. Flamant in 1892 by modifying the three-dimensional solution of Boussinesq.

Vincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty (1975a). They are based on the assumption that the figure of the Earth is an oblate spheroid, and hence are more accurate than methods that assume a spherical Earth, such as great-circle distance.

In analytical mechanics, the mass matrix is a symmetric matrix M that expresses the connection between the time derivative of the generalized coordinate vector q of a system and the kinetic energy T of that system, by the equation

In solid mechanics, the Johnson–Holmquist damage model is used to model the mechanical behavior of damaged brittle materials, such as ceramics, rocks, and concrete, over a range of strain rates. Such materials usually have high compressive strength but low tensile strength and tend to exhibit progressive damage under load due to the growth of microfractures.

Plate theory mathematical descriptions of the mechanics of flat plates

In continuum mechanics, plate theories are mathematical descriptions of the mechanics of flat plates that draws on the theory of beams. Plates are defined as plane structural elements with a small thickness compared to the planar dimensions. The typical thickness to width ratio of a plate structure is less than 0.1. A plate theory takes advantage of this disparity in length scale to reduce the full three-dimensional solid mechanics problem to a two-dimensional problem. The aim of plate theory is to calculate the deformation and stresses in a plate subjected to loads.

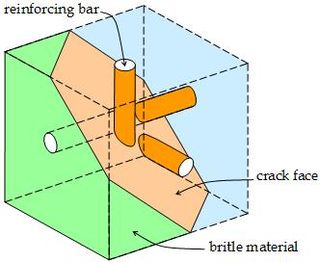
Reinforced solid

In solid mechanics, a reinforced solid is a brittle material that is reinforced by ductile bars or fibres. A common application is reinforced concrete. When the concrete cracks the tensile force in a crack is not carried any more by the concrete but by the steel reinforcing bars only. The reinforced concrete will continue to carry the load provided that sufficient reinforcement is present. A typical design problem is to find the smallest amount of reinforcement that can carry the stresses on a small cube. This can be formulated as an optimization problem.

In fluid dynamics, Taylor scraping flow is a type of two-dimensional corner flow occurring when one of the wall is sliding over the other with constant velocity, named after G. I. Taylor.

References

  1. ↑ Hankinson, R. L., 1921, Investigation of crushing strength of spruce at varying angles of grain, Air Force Information Circular No. 259, U. S. Air Service.
  2. ↑ Clouston, P., 1995, The Tsai-Wu strength theory for Douglas fir laminated veneer , M. S. Thesis, The University of British Columbia.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.