Herman ring

Last updated July 20, 2023

In the mathematical discipline known as complex dynamics, the Herman ring is a Fatou component ^[1] where the rational function is conformally conjugate to an irrational rotation of the standard annulus.

Formal definition

Namely if ƒ possesses a Herman ring U with period p, then there exists a conformal mapping

\phi :U\rightarrow \{\zeta :0<r<|\zeta |<1\}

and an irrational number $\theta$ , such that

\phi \circ f^{\circ p}\circ \phi ^{-1}(\zeta )=e^{2\pi i\theta }\zeta .

So the dynamics on the Herman ring is simple.

Name

It was introduced by, and later named after, Michael Herman (1979^[2]) who first found and constructed this type of Fatou component.

Function

Polynomials do not have Herman rings.
Rational functions can have Herman rings. According to the result of Shishikura, if a rational function ƒ possesses a Herman ring, then the degree of ƒ is at least 3.
Transcendental entire maps do not have them^[3]
meromorphic functions can possess Herman rings. Herman rings for transcendental meromorphic functions have been studied by T. Nayak. According to a result of Nayak, if there is an omitted value for such a function then Herman rings of period 1 or 2 do not exist. Also, it is proved that if there is only a single pole and at least an omitted value, the function has no Herman ring of any period.

Examples

Herman and parabolic basin

Here is an example of a rational function which possesses a Herman ring.^[1]

f(z)={\frac {e^{2\pi i\tau }z^{2}(z-4)}{1-4z}}

where $\tau =0.6151732\dots$ such that the rotation number of ƒ on the unit circle is $({\sqrt {5}}-1)/2$ .

The picture shown on the right is the Julia set of ƒ: the curves in the white annulus are the orbits of some points under the iterations of ƒ while the dashed line denotes the unit circle.

There is an example of rational function that possesses a Herman ring, and some periodic parabolic Fatou components at the same time.

A rational function
f
t
,
a
,
b
(
z
)
=
e
2
p
i
t
z
3
1
-
a
-
z
z
-
a
1
-
b
-
z
z
-
b
{\displaystyle f_{t,a,b}(z)=e^{2\pi it}z^{3}\,{\frac {1-{\overline {a}}z}{z-a}}\,{\frac {1-{\overline {b}}z}{z-b}}}
that possesses a Herman ring and some periodic parabolic Fatou components, where
t
=
0.6141866
...
,
a
=
1
/
4
,
b
=
0.0405353
-
0.0255082
i
{\displaystyle t=0.6141866\dots ,\,a=1/4,\,b=0.0405353-0.0255082i}
such that the rotation number of
f
t
,
a
,
b
{\displaystyle f_{t,a,b}}
on the unit circle is
(
5
-
1
)
/
2
{\displaystyle ({\sqrt {5}}-1)/2}
. The image has been rotated. Herman+Parabolic.png — A rational function $f_{t,a,b}(z)=e^{2\pi it}z^{3}\,{\frac {1-{\overline {a}}z}{z-a}}\,{\frac {1-{\overline {b}}z}{z-b}}$ that possesses a Herman ring and some periodic parabolic Fatou components, where $t=0.6141866\dots ,\,a=1/4,\,b=0.0405353-0.0255082i$ such that the rotation number of $f_{t,a,b}$ on the unit circle is $({\sqrt {5}}-1)/2$ . The image has been rotated.

Period 2 Herman ring

Further, there is a rational function which possesses a Herman ring with period 2.

Here the expression of this rational function is

g_{a,b,c}(z)={\frac {z^{2}(z-a)}{z-b}}+c,\,

where

{\begin{aligned}a&=0.17021425+0.12612303i,\\b&=0.17115266+0.12592514i,\\c&=-1.18521775-0.16885254i.\end{aligned}}

This example was constructed by quasiconformal surgery^[4] from the quadratic polynomial

h(z)=z^{2}-1-{\frac {e^{{\sqrt {5}}\pi i}}{4}}

which possesses a Siegel disk with period 2. The parameters a, b, c are calculated by trial and error.

Letting

{\begin{aligned}a&=0.14285933+0.06404502i,\\b&=0.14362386+0.06461542i,{\text{ and}}\\c&=-0.18242894-0.81957139i,\end{aligned}}

then the period of one of the Herman ring of g_a,b,c is 3.

Shishikura also given an example:^[5] a rational function which possesses a Herman ring with period 2, but the parameters showed above are different from his.

Period 5 Herman ring

So there is a question: How to find the formulas of the rational functions which possess Herman rings with higher period?

This question can be answered (for any period > 0) by using the Mandelbrot set for the rational functions g_a,b,c. The classic Mandelbrot set (for quadratic polynomials) is approximated by iterating the critical point for each such polynomial, and identifying the polynomials for which the iterates of the critical point do not converge to infinity. Similarly a Mandelbrot set can be defined for the set of rational functions g_a,b,c by distinguishing between the values of (a,b,c) in complex 3-space for which all the three critical points (i.e. points where the derivative vanishes) of the function converge to infinity, and the values whose critical points do not all converge to infinity.

For each value of a and b, the Mandelbrot set for g_a,b,ccan be calculated in the plane of complex values c. When a and b are nearly equal, this set approximates the classic Mandelbrot set for quadratic polynomials, because g_a,b,c is equal to x² + c when a=b. In the classic Mandelbrot set, Siegel discs can be approximated by choosing points along the edge of the Mandelbrot set with irrational winding number having continued fraction expansion with bounded denominators. The irrational numbers are of course only approximated in their computer representation. These denominators can be identified by the sequence of nodes along the edge of the Mandelbrot set approaching the point. Similarly, Herman rings can be identified in a Mandelbrot set of rational functions by observing a series of nodes arranged on both sides of a curve, and choosing points along that curve, avoiding the attached nodes, thereby obtaining a desired sequence of denominators in the continued fraction expansion of the rotation number. The following illustrates a planar slice of the Mandelbrot set of g_a,b,c with |a-b| = .0001, and with c centered at a value of c which identifies a 5-cycle of Siegel discs in the classic Mandelbrot set.

Mandelbrot set of the rational function g, in the c-plane, near 5-cycles. 5CycleMset.png — Mandelbrot set of the rational function g, in the c-plane, near 5-cycles.

The image above uses a =0.12601278 +.0458649i, b= .12582484 +.045796497i, and is centered at a value of c = 0.3688 -.3578, which is near 5-cycles of Siegel discs in the classic Mandelbrot set. In the above image, a 5-cycle of Herman rings can be approximated by choosing a point c along the above illustrated curve having nodes on both sides, for which g_a,b,c has approximately the desired winding number, using values as follows:

${\begin{aligned}a&=.12601278+.0458649i,\\b&=.12582484+.045796497i,{\text{ and}}\\c&=0.37144067-.35829275i,\end{aligned}}$

The resulting 5-cycle of Herman rings is illustrated below:

Julia set of g showing a period 5 Herman ring. 5CycleHerman.png — Julia set of g showing a period 5 Herman ring.

Related Research Articles

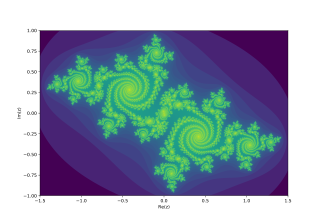
The Mandelbrot set is a two dimensional set with a relatively simple definition that exhibits great complexity, especially as it is magnified. It is popular for its aesthetic appeal and fractal structures. The set is defined in the complex plane as complex numbers $for which the function does not diverge to infinity when iterated starting at, i.e., for which the sequence,, etc., remains bounded in absolute value.$

In number theory, a multiplicative function is an arithmetic function f(n) of a positive integer n with the property that f(1) = 1 and

The fundamental theorem of algebra, also known as d'Alembert's theorem, or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero.

In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".

In algebraic number theory, an algebraic integer is a complex number which is integral over the integers. That is, an algebraic integer is a complex root of some monic polynomial whose coefficients are integers. The set of all algebraic integers $A$ is closed under addition, subtraction and multiplication and therefore is a commutative subring of the complex numbers.

<span class="mw-page-title-main">Hurwitz zeta function</span> Special function in mathematics

In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables $s$ with $Re(s) > 1$ and $a \neq 0, -1, -2, \dots$ by

The Basel problem is a problem in mathematical analysis with relevance to number theory, concerning an infinite sum of inverse squares. It was first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up years later by Bernhard Riemann in his seminal 1859 paper "On the Number of Primes Less Than a Given Magnitude", in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.

This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.

In mathematics, Apéry's theorem is a result in number theory that states the Apéry's constant ζ(3) is irrational. That is, the number

In mathematics, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number

In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function f of a complex argument z and an operator T, the aim is to construct an operator, f(T), which naturally extends the function f from complex argument to operator argument. More precisely, the functional calculus defines a continuous algebra homomorphism from the holomorphic functions on a neighbourhood of the spectrum of T to the bounded operators.

$<span class="mw-page-title-main">Newton fractal</span> Boundary set in the complex plane$

The Newton fractal is a boundary set in the complex plane which is characterized by Newton's method applied to a fixed polynomial $p (Z) \in ℂ[Z]$ or transcendental function. It is the Julia set of the meromorphic function $z \mapsto z - p (z) / p' (z)$ which is given by Newton's method. When there are no attractive cycles (of order greater than 1), it divides the complex plane into regions $G k$ , each of which is associated with a root $ζ k$ of the polynomial, $k = 1, \dots, deg(p)$ . In this way the Newton fractal is similar to the Mandelbrot set, and like other fractals it exhibits an intricate appearance arising from a simple description. It is relevant to numerical analysis because it shows that (outside the region of quadratic convergence) the Newton method can be very sensitive to its choice of start point.

Mitsuhiro Shishikura is a Japanese mathematician working in the field of complex dynamics. He is professor at Kyoto University in Japan.

In mathematics, Fatou components are components of the Fatou set. They were named after Pierre Fatou.

In the metrical theory of regular continued fractions, the kth complete quotient ζ_k is obtained by ignoring the first k partial denominators a_i. For example, if a regular continued fraction is given by

A complex quadratic polynomial is a quadratic polynomial whose coefficients and variable are complex numbers.

A Siegel disc or Siegel disk is a connected component in the Fatou set where the dynamics is analytically conjugate to an irrational rotation.

In number theory, an average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".

In mathematics, an algebraic number field is an extension field $of the field of rational numbers such that the field extension has finite degree . Thus is a field that contains and has finite dimension when considered as a vector space over .$

<span class="mw-page-title-main">Riemann sphere</span> Model of the extended complex plane plus a point at infinity

In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value $for infinity. With the Riemann model, the point is near to very large numbers, just as the point is near to very small numbers.$

References

1 2 John Milnor, Dynamics in one complex variable: Third Edition, Annals of Mathematics Studies, 160, Princeton Univ. Press, Princeton, NJ, 2006.
↑ Herman, Michael-Robert (1979), "Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations", Publications Mathématiques de l'IHÉS , 49 (49): 5–233, doi:10.1007/BF02684798, ISSN 1618-1913, MR 0538680, S2CID 118356096
↑ Omitted Values and Herman rings by Tarakanta Nayak.^{[ full citation needed ]}
↑ Mitsuhiro Shishikura, On the quasiconformal surgery of rational functions. Ann. Sci. Ecole Norm. Sup. (4) 20 (1987), no. 1, 1–29.
↑ Mitsuhiro Shishikura, Surgery of complex analytic dynamical systems, in "Dynamical Systems and Nonlinear Oscillations", Ed. by Giko Ikegami, World Scientific Advanced Series in Dynamical Systems, 1, World Scientific, 1986, 93–105.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[dyn-1] 1 2 John Milnor, Dynamics in one complex variable: Third Edition, Annals of Mathematics Studies, 160, Princeton Univ. Press, Princeton, NJ, 2006.

[2] Herman, Michael-Robert (1979), "Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations", Publications Mathématiques de l'IHÉS , 49 (49): 5–233, doi:10.1007/BF02684798, ISSN 1618-1913, MR 0538680, S2CID 118356096

[3] Omitted Values and Herman rings by Tarakanta Nayak.^{[ full citation needed ]}

[4] Mitsuhiro Shishikura, On the quasiconformal surgery of rational functions. Ann. Sci. Ecole Norm. Sup. (4) 20 (1987), no. 1, 1–29.

[5] Mitsuhiro Shishikura, Surgery of complex analytic dynamical systems, in "Dynamical Systems and Nonlinear Oscillations", Ed. by Giko Ikegami, World Scientific Advanced Series in Dynamical Systems, 1, World Scientific, 1986, 93–105.

[1]

[2]

[3]

[4]

[5]