 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages)
|
Linear control are control systems and control theory based on negative feedback for producing a control signal to maintain the controlled process variable (PV) at the desired setpoint (SP). There are several types of linear control systems with different capabilities.
Proportional control is a type of linear feedback control system in which a correction is applied to the controlled variable which is proportional to the difference between the desired value (SP) and the measured value (PV). Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor.
The proportional control system is more complex than an on–off control system but simpler than a proportional-integral-derivative (PID) control system used, for instance, in an automobile cruise control. On–off control will work for systems that do not require high accuracy or responsiveness but are not effective for rapid and timely corrections and responses. Proportional control overcomes this by modulating the manipulated variable (MV), such as a control valve, at a gain level that avoids instability, but applies correction as fast as practicable by applying the optimum quantity of proportional correction.
A drawback of proportional control is that it cannot eliminate the residual SP–PV error, as it requires an error to generate a proportional output. A PI controller can be used to overcome this. The PI controller uses a proportional term (P) to remove the gross error, and an integral term (I) to eliminate the residual offset error by integrating the error over time.
In some systems, there are practical limits to the range of the MV. For example, a heater has a limit to how much heat it can produce and a valve can open only so far. Adjustments to the gain simultaneously alter the range of error values over which the MV is between these limits. The width of this range, in units of the error variable and therefore of the PV, is called the proportional band (PB).
When controlling the temperature of an industrial furnace, it is usually better to control the opening of the fuel valve in proportion to the current needs of the furnace. This helps avoid thermal shocks and applies heat more effectively.
At low gains, only a small corrective action is applied when errors are detected. The system may be safe and stable but may be sluggish in response to changing conditions. Errors will remain uncorrected for relatively long periods of time and the system is overdamped. If the proportional gain is increased, such systems become more responsive and errors are dealt with more quickly. There is an optimal value for the gain setting when the overall system is said to be critically damped. Increases in loop gain beyond this point lead to oscillations in the PV and such a system is underdamped. Adjusting gain to achieve critically damped behavior is known as tuning the control system.
In the underdamped case, the furnace heats quickly. Once the setpoint is reached, stored heat within the heater sub-system and in the walls of the furnace will keep the measured temperature rising beyond what is required. After rising above the setpoint, the temperature falls back and eventually heat is applied again. Any delay in reheating the heater sub-system allows the furnace temperature to fall further below the setpoint and the cycle repeats. The temperature oscillations that an underdamped furnace control system produces are undesirable.
In a critically damped system, as the temperature approaches the setpoint, the heat input begins to be reduced, the rate of heating of the furnace has time to slow and the system avoids overshoot. Overshoot is also avoided in an overdamped system but an overdamped system is unnecessarily slow to initially reach a setpoint response to external changes to the system, e.g. opening the furnace door.
Pure proportional controllers must operate with residual error in the system. Though PI controllers eliminate this error they can still be sluggish or produce oscillations. The PID controller addresses these final shortcomings by introducing a derivative (D) action to retain stability while responsiveness is improved.
The derivative is concerned with the rate-of-change of the error with time: If the measured variable approaches the setpoint rapidly, then the actuator is backed off early to allow it to coast to the required level; conversely, if the measured value begins to move rapidly away from the setpoint, extra effort is applied—in proportion to that rapidity to help move it back.
On control systems involving motion control of a heavy item like a gun or camera on a moving vehicle, the derivative action of a well-tuned PID controller can allow it to reach and maintain a setpoint better than most skilled human operators. If a derivative action is over-applied, it can, however, lead to oscillations.
The integral term magnifies the effect of long-term steady-state errors, applying an ever-increasing effort until the error is removed. In the example of the furnace above working at various temperatures, if the heat being applied does not bring the furnace up to setpoint, for whatever reason, integral action increasingly moves the proportional band relative to the setpoint until the PV error is reduced to zero and the setpoint is achieved.
Some controllers include the option to limit the "ramp up % per minute". This option can be very helpful in stabilizing small boilers (3 MBTUH), especially during the summer, during light loads. A utility boiler "unit may be required to change load at a rate of as much as 5% per minute (IEA Coal Online - 2, 2007)". [1] [ failed verification ]
It is possible to filter the PV or error signal. Doing so can help reduce instability or oscillations by reducing the response of the system to undesirable frequencies. Many systems have a resonant frequency. By filtering out that frequency, stronger overall feedback can be applied before oscillation occurs, making the system more responsive without shaking itself apart.
Feedback systems can be combined. In cascade control, one control loop applies control algorithms to a measured variable against a setpoint but then provides a varying setpoint to another control loop rather than affecting process variables directly. If a system has several different measured variables to be controlled, separate control systems will be present for each of them.
Control engineering in many applications produces control systems that are more complex than PID control. Examples of such field applications include fly-by-wire aircraft control systems, chemical plants, and oil refineries. Model predictive control systems are designed using specialized computer-aided-design software and empirical mathematical models of the system to be controlled.
Control engineering or control systems engineering is an engineering discipline that deals with control systems, applying control theory to design equipment and systems with desired behaviors in control environments. The discipline of controls overlaps and is usually taught along with electrical engineering and mechanical engineering at many institutions around the world.
Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
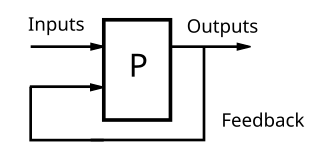
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to feed back into itself. The notion of cause-and-effect has to be handled carefully when applied to feedback systems:
Simple causal reasoning about a feedback system is difficult because the first system influences the second and second system influences the first, leading to a circular argument. This makes reasoning based upon cause and effect tricky, and it is necessary to analyze the system as a whole. As provided by Webster, feedback in business is the transmission of evaluative or corrective information about an action, event, or process to the original or controlling source.
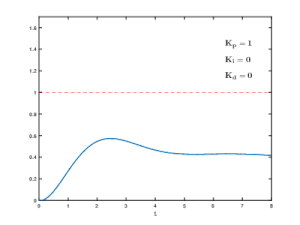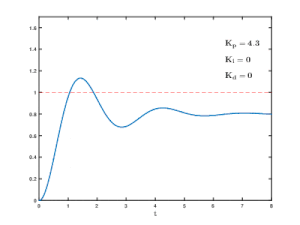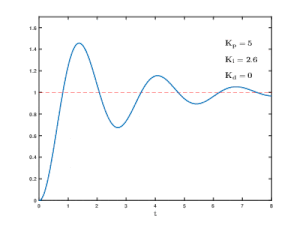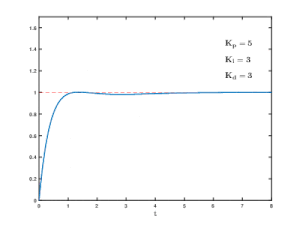
A proportional–integral–derivative controller is a control loop mechanism employing feedback that is widely used in industrial control systems and a variety of other applications requiring continuously modulated control. A PID controller continuously calculates an error value as the difference between a desired setpoint (SP) and a measured process variable (PV) and applies a correction based on proportional, integral, and derivative terms, hence the name.
Negative feedback occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances.
A thermostat is a regulating device component which senses the temperature of a physical system and performs actions so that the system's temperature is maintained near a desired setpoint.
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling processes or machines. The control systems are designed via control engineering process.
A closed-loop controller or feedback controller is a control loop which incorporates feedback, in contrast to an open-loop controller or non-feedback controller. A closed-loop controller uses feedback to control states or outputs of a dynamical system. Its name comes from the information path in the system: process inputs have an effect on the process outputs, which is measured with sensors and processed by the controller; the result is "fed back" as input to the process, closing the loop.
In control theory, an open-loop controller, also called a non-feedback controller, is a control loop part of a control system in which the control action is independent of the "process output", which is the process variable that is being controlled. It does not use feedback to determine if its output has achieved the desired goal of the input command or process setpoint.
An industrial process control or simply process control in continuous production processes is a discipline that uses industrial control systems and control theory to achieve a production level of consistency, economy and safety which could not be achieved purely by human manual control. It is implemented widely in industries such as automotive, mining, dredging, oil refining, pulp and paper manufacturing, chemical processing and power generating plants.
In cybernetics and control theory, a setpoint is the desired or target value for an essential variable, or process value (PV) of a control system. Departure of such a variable from its setpoint is one basis for error-controlled regulation using negative feedback for automatic control.
Temperature control is a process in which change of temperature of a space, or of a substance, is measured or otherwise detected, and the passage of heat energy into or out of the space or substance is adjusted to achieve a desired temperature.
Proportional control, in engineering and process control, is a type of linear feedback control system in which a correction is applied to the controlled variable, and the size of the correction is proportional to the difference between the desired value and the measured value. Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor.
Nonlinear control theory is the area of control theory which deals with systems that are nonlinear, time-variant, or both. Control theory is an interdisciplinary branch of engineering and mathematics that is concerned with the behavior of dynamical systems with inputs, and how to modify the output by changes in the input using feedback, feedforward, or signal filtering. The system to be controlled is called the "plant". One way to make the output of a system follow a desired reference signal is to compare the output of the plant to the desired output, and provide feedback to the plant to modify the output to bring it closer to the desired output.
A control loop is the fundamental building block of control systems in general industrial control systems and industrial control systems in particular. It consists of the process sensor, the controller function, and the final control element (FCE) which controls the process necessary to automatically adjust the value of a measured process variable (PV) to equal the value of a desired set-point (SP).
Integral windup, also known as integrator windup or reset windup, refers to the situation in a PID controller where a large change in setpoint occurs and the integral term accumulates a significant error during the rise (windup), thus overshooting and continuing to increase as this accumulated error is unwound. The specific problem is the excess overshooting.
In control theory, a bang–bang controller, is a feedback controller that switches abruptly between two states. These controllers may be realized in terms of any element that provides hysteresis. They are often used to control a plant that accepts a binary input, for example a furnace that is either completely on or completely off. Most common residential thermostats are bang–bang controllers. The Heaviside step function in its discrete form is an example of a bang–bang control signal. Due to the discontinuous control signal, systems that include bang–bang controllers are variable structure systems, and bang–bang controllers are thus variable structure controllers.
In control theory, a process variable is the current measured value of a particular part of a process which is being monitored or controlled. An example of this would be the temperature of a furnace. The current temperature is the process variable, while the desired temperature is known as the set-point (SP).
Active disturbance rejection control inherits from proportional–integral–derivative (PID). It embraces the power of nonlinear feedback and puts it to full use. It is a robust control method that is based on extension of the system model with an additional and fictitious state variable, representing everything that the user does not include in the mathematical description of the plant. This virtual state is estimated online with a state eyewitness and used in the control signal in order to decouple the system from the actual perturbation acting on the plant. This disturbance rejection feature allows user to treat the considered system with a simpler model, since the negative effects of modeling uncertainty are compensated in real time. As a result, the operator does not need a precise analytical description of the system, as one can assume the unknown parts of dynamics as the internal disturbance in the plant. Robustness and the adaptive ability of this method makes it an interesting solution in scenarios where the full knowledge of the system is not available.
Classical control theory is a branch of control theory that deals with the behavior of dynamical systems with inputs, and how their behavior is modified by feedback, using the Laplace transform as a basic tool to model such systems.
