Related Research Articles
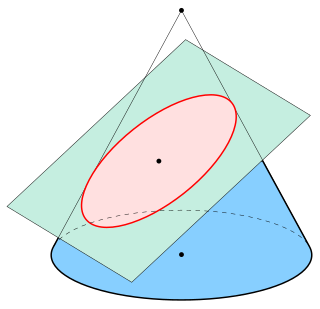
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .

In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.

In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz.

In Newtonian mechanics, momentum is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If m is an object's mass and v is its velocity, then the object's momentum p is:
In physics, power is the amount of energy transferred or converted per unit time. In the International System of Units, the unit of power is the watt, equal to one joule per second. In older works, power is sometimes called activity. Power is a scalar quantity.

In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors, dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix.

An electric field is the physical field that surrounds electrically charged particles. Charged particles exert attractive forces on each other when their charges are opposite, and repulsion forces on each other when their charges are the same. Because these forces are exerted mutually, 2 charges must be present for the forces to take place. The electric field of a single charge describes their capacity to exert such forces on another charged object. These forces are described by Coulomb's Law, which says that the greater the magnitude of the charges, the greater the force, and the greater the distance between them, the weaker the force. Thus, we may informally say that the greater the charge of an object, the stronger its electric field. Similarly, the electric field is stronger nearer charged objects and weaker further away. Electric fields originate from electric charges and time-varying electric currents. Electric fields and magnetic fields are both manifestations of the electromagnetic field, one of the four fundamental forces of nature.

In electrical engineering, impedance is the opposition to alternating current presented by the combined effect of resistance and reactance in a circuit.
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In physics, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the product of the force strength and the distance traveled. A force is said to do positive work if when applied it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.
Some Buddhist terms and concepts lack direct translations into English that cover the breadth of the original term. Below are given a number of important Buddhist terms, short definitions, and the languages in which they appear. In this list, an attempt has been made to organize terms by their original form and give translations and synonyms in other languages along with the definition.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure-volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as

In biochemistry, Michaelis–Menten kinetics, named after Leonor Michaelis and Maud Menten, is the simplest case of enzyme kinetics, applied to enzyme-catalysed reactions of one substrate and one product. It takes the form of an equation describing the reaction rate to , the concentration of the substrate A. Its formula is given by the Michaelis–Menten equation:
Time dilation is the difference in elapsed time as measured by two clocks, either due to a relative velocity between them, or a difference in gravitational potential between their locations. When unspecified, "time dilation" usually refers to the effect due to velocity.
In fluid dynamics, drag is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers or between a fluid and a solid surface.
In linear algebra, it is often important to know which vectors have their directions unchanged by a linear transformation. An eigenvector or characteristic vector is such a vector. Thus an eigenvector of a linear transformation is scaled by a constant factor when the linear transformation is applied to it: . The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor .

A capacitor is an electronic device that stores electrical energy in an electric field by accumulating electric charges on two closely spaced surfaces that are insulated from each other. It is a passive electronic component with two terminals.

Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery and astronomical objects, such as spacecraft, planets, stars, and galaxies. The "classical" in "classical mechanics" does not refer to classical antiquity, as it might in, say, classical architecture. On the contrary, the development of classical mechanics involved substantial change in the methods and philosophy of physics. Instead, the qualifier distinguishes classical mechanics from physics developed after the revolutions of the early 20th century, which revealed limitations of classical mechanics.

Velocity is the speed in combination with the direction of motion of an object. Velocity is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of bodies.

In mathematics, Hilbert spaces allow the methods of linear algebra and calculus to be generalized from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that induces a distance function for which the space is a complete metric space.