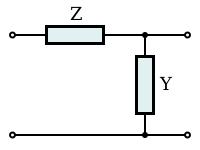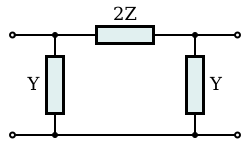M-derived filter

Parts of this article or section rely on the reader's knowledge of the complex impedance representation of capacitors and inductors and on knowledge of the frequency domain representation of signals.

m-derived filters or m-type filters are a type of electronic filter designed using the image method. They were invented by Otto Zobel in the early 1920s. ^[1] This filter type was originally intended for use with telephone multiplexing and was an improvement on the existing constant k type filter. ^[2] The main problem being addressed was the need to achieve a better match of the filter into the terminating impedances. In general, all filters designed by the image method fail to give an exact match, but the m-type filter is a big improvement with suitable choice of the parameter m. The m-type filter section has a further advantage in that there is a rapid transition from the cut-off frequency of the passband to a pole of attenuation just inside the stopband. Despite these advantages, there is a drawback with m-type filters; at frequencies past the pole of attenuation, the response starts to rise again, and m-types have poor stopband rejection. For this reason, filters designed using m-type sections are often designed as composite filters with a mixture of k-type and m-type sections and different values of m at different points to get the optimum performance from both types. ^[3]

Midpoint impedance

The parameter m is given this symbol because of its association with midpoint impedance, a concept used by Zobel in his original treatment of the subject. Midpoint impedance arises in the following way. In this article and most modern textbooks, the starting point is the simple half-section, and more complex filters are built up from this. In Zobel's treatment and that of his contemporaries, the starting point is always the infinite ladder network. A "mid-series" section is derived by "cutting through the middle" of the series impedance Z and results in a T section. The image impedance ZiT is referred to as the mid-series image impedance. Similarly, a "mid-shunt" section is derived by cutting through the middle of the shunt admittance Y and results in a Π section with a mid-shunt image impedance. A "series m-derived section" is shorthand for "mid-series derived ladder type section". This makes it clear that the word series is referring to the ends of the T section being (half) a series component and not as is sometimes thought, because the additional component is in series with the shunt element. Similarly, "shunt m-derived section" is shorthand for "mid-shunt derived ladder type section". [4]

Background

Zobel patented an impedance matching network in 1920 ^[5] which, in essence, used the topology of what are now called m-type filters, but Zobel did not name them as such or analyse them by the image method. This pre-dated George Campbell's publication of his constant k-type design in 1922 on which the m-type filter is based. ^[6] Zobel published the image analysis theory of m-type filters in 1923. ^[7] Once popular, M-type filters and image parameter designed filters in general are now rarely designed, having been superseded by more advanced network synthesis methods. ^[8]

Derivation

m-derived series general filter half section

m-derived shunt low-pass filter half section.
${\displaystyle C={\frac {L}{R_{0}^{2}}}}$

The building block of m-derived filters, as with all image impedance filters, is the "L" network, called a half-section and composed of a series impedance Z, and a shunt admittance Y. The m-derived filter is a derivative of the constant k filter. The starting point of the design is the values of Z and Y derived from the constant k prototype and are given by

${\displaystyle k^{2}={\frac {Z}{Y}}}$

where k is the nominal impedance of the filter, or R₀. The designer now multiplies Z and Y by an arbitrary constant m (0 < m < 1). There are two different kinds of m-derived section; series and shunt. To obtain the m-derived series half section, the designer determines the impedance that must be added to 1/mY to make the image impedance Z_iT the same as the image impedance of the original constant k section. From the general formula for image impedance, the additional impedance required can be shown to be ^[9]

${\displaystyle {\frac {1-m^{2}}{m}}Z.}$

To obtain the m-derived shunt half section, an admittance is added to 1/mZ to make the image impedance Z_iΠ the same as the image impedance of the original half section. The additional admittance required can be shown to be ^[10]

${\displaystyle {\frac {1-m^{2}}{m}}Y.}$

The general arrangements of these circuits are shown in the diagrams to the right along with a specific example of a low-pass section.

A consequence of this design is that the m-derived half section will match a k-type section on one side only. Also, an m-type section of one value of m will not match another m-type section of another value of m except on the sides which offer the Z_i of the k-type. ^[11]

Operating frequency

For the low-pass half section shown, the cut-off frequency of the m-type is the same as the k-type and is given by

${\displaystyle \omega _{c}={\frac {1}{\sqrt {LC}}}.}$

The pole of attenuation occurs at;

${\displaystyle \omega _{\infty }={\frac {\omega _{c}}{\sqrt {1-m^{2}}}}.}$

From this it is clear that smaller values of m will produce ${\displaystyle \omega _{\infty }}$ closer to the cut-off frequency ${\displaystyle \omega _{c}\,\!}$ and hence will have a sharper cut-off. Despite this cut-off, it also brings the unwanted stopband response of the m-type closer to the cut-off frequency, making it more difficult for this to be filtered with subsequent sections. The value of m chosen is usually a compromise between these conflicting requirements. There is also a practical limit to how small m can be made due to the inherent resistance of the inductors. This has the effect of causing the pole of attenuation to be less deep (that is, it is no longer a genuinely infinite pole) and the slope of cut-off to be less steep. This effect becomes more marked as ${\displaystyle \omega _{\infty }}$ is brought closer to ${\displaystyle \omega _{c}\,\!}$, and there ceases to be any improvement in response with an m of about 0.2 or less. ^{[11] [12] [13]}

Image impedance

See also: Image impedance § Derivation

m-derived prototype shunt low-pass filter Z_iTm image impedance for various values of m. Values below cut-off frequency only shown for clarity.

The following expressions for image impedances are all referenced to the low-pass prototype section. They are scaled to the nominal impedance R₀ = 1, and the frequencies in those expressions are all scaled to the cut-off frequency ω_c = 1.

Series sections

The image impedances of the series section are given by ^[14]

${\displaystyle Z_{iT}={\sqrt {1-\omega ^{2}}}}$

and is the same as that of the constant k section

${\displaystyle Z_{i\Pi m}={\frac {1-\left(\omega /\omega _{\infty }\right)^{2}}{\sqrt {1-\omega ^{2}}}}.}$

Shunt sections

The image impedances of the shunt section are given by ^[11]

${\displaystyle Z_{i\Pi }={\frac {1}{\sqrt {1-\omega ^{2}}}}}$

and is the same as that of the constant k section

${\displaystyle Z_{iTm}={\frac {\sqrt {1-\omega ^{2}}}{1-\left(\omega /\omega _{\infty }\right)^{2}}}}$

As with the k-type section, the image impedance of the m-type low-pass section is purely real below the cut-off frequency and purely imaginary above it. From the chart it can be seen that in the passband the closest impedance match to a constant pure resistance termination occurs at approximately m = 0.6. ^[14]

Transmission parameters

See also: Image impedance § Transfer function

m-Derived low-pass filter transfer function for a single half-section

For an m-derived section in general the transmission parameters for a half-section are given by ^[14]

${\displaystyle \gamma =\sinh ^{-1}{\frac {mZ}{\sqrt {k^{2}+(1-m^{2})Z^{2}}}}}$

and for n half-sections

${\displaystyle \gamma _{n}=n\gamma \,\!}$

For the particular example of the low-pass L section, the transmission parameters solve differently in three frequency bands. ^[14]

For ${\displaystyle 0<\omega <\omega _{c}\,\!}$ the transmission is lossless:

${\displaystyle \gamma =\alpha +i\beta =0+i{\frac {1}{2}}\cos ^{-1}\left(1-{\frac {2m^{2}}{\left({\frac {\omega _{c}}{\omega }}\right)^{2}-\left({\frac {\omega _{c}}{\omega _{\infty }}}\right)^{2}}}\right)}$

For ${\displaystyle \omega _{c}<\omega <\omega _{\infty }}$ the transmission parameters are

${\displaystyle \gamma =\alpha +i\beta ={\frac {1}{2}}\cosh ^{-1}\left({\frac {2m^{2}}{\left({\frac {\omega _{c}}{\omega }}\right)^{2}-\left({\frac {\omega _{c}}{\omega _{\infty }}}\right)^{2}}}-1\right)+i{\frac {\pi }{2}}}$

For ${\displaystyle \omega _{\infty }<\omega <\infty }$ the transmission parameters are

${\displaystyle \gamma =\alpha +i\beta ={\frac {1}{2}}\cosh ^{-1}\left(1-{\frac {2m^{2}}{\left({\frac {\omega _{c}}{\omega }}\right)^{2}-\left({\frac {\omega _{c}}{\omega _{\infty }}}\right)^{2}}}\right)+i0}$

Prototype transformations

The plots shown of image impedance, attenuation and phase change are the plots of a low-pass prototype filter section. The prototype has a cut-off frequency of ω_c = 1 rad/s and a nominal impedance R₀ = 1 Ω. This is produced by a filter half-section where L = 1 henry and C = 1 farad. This prototype can be impedance scaled and frequency scaled to the desired values. The low-pass prototype can also be transformed into high-pass, band-pass or band-stop types by application of suitable frequency transformations. ^[15]

Cascading sections

Several L half-sections may be cascaded to form a composite filter. Like impedance must always face like in these combinations. There are therefore two circuits that can be formed with two identical L half-sections. Where Z_iT faces Z_iT, the section is called a Π section. Where Z_iΠ faces Z_iΠ the section formed is a T section. Further additions of half-sections to either of these forms a ladder network which may start and end with series or shunt elements. ^[16]

It should be born in mind that the characteristics of the filter predicted by the image method are only accurate if the section is terminated with its image impedance. This is usually not true of the sections at either end which are usually terminated with a fixed resistance. The further the section is from the end of the filter, the more accurate the prediction will become since the effects of the terminating impedances are masked by the intervening sections. It is usual to provide half half-sections at the ends of the filter with m = 0.6 as this value gives the flattest Z_i in the passband and hence the best match in to a resistive termination. ^[17]

Image filter sections
	Unbalanced L Half section T Section Π Section Ladder network
	Balanced C Half-section H Section Box Section Ladder network X Section (mid-T-Derived) X Section (mid-Π-Derived)
N.B. Textbooks and design drawings usually show the unbalanced implementations, but in telecoms it is often required to convert the design to the balanced implementation when used with balanced lines. edit

See also

• Image impedance
• Constant k filter
• General m_n-type image filters
• mm'-type filter
• Composite image filter

References

1. Belevitch, V, "Summary of the history of circuit theory", Proceedings of the IRE, vol 50, Iss 5, pp.849, May 1962.
2. Bray, J, Innovation and the Communications Revolution, p.62, Institute of Electrical Engineers, 2002 ISBN   0-85296-218-5.
3. Zobel, pp. 16–19.
4. Zobel, O J, Electrical wave filters, U.S. Patent 1,850,146 , pp. 2–3, filed 25 Nov 1930, issued 22 March 1932.
5. Zobel, O J, Terminating network for filters, U.S. Patent 1,557,229 , filed 30 April 1920, issued 13 October 1925.
6. Campbell, G A, "Physical Theory of the Electric Wave-Filter", Bell System Tech J, November 1922, vol 1, no 2, pp. 1–32.
7. Zobel, O. J.,Theory and Design of Uniform and Composite Electric Wave Filters, Bell System Technical Journal, Vol. 2 (1923), pp. 1–46.
8. Roberto Sorrentino, Electronic filter simulation & design, p. 57, McGraw-Hill Professional, 2007 ISBN   0-07-149467-7.
9. Matthaei, p. 64.
10. Matthaei, p.66.
11. Matthaei, p. 65.
12. Bode, Hendrik W., Wave Filter, U.S. Patent 2,002,216 , p. 1 c. 1 ll.14–26, filed 7 June 1933, issued 21 May 1935.
13. Alan Keith Walton, Network analysis and practice, pp. 197, 203, Cambridge University Press, 1987 ISBN   0-521-31903-X.
14. Matthaei, p. 63.
15. Matthaei, pp. 60–61 (LPF), 412 (HPF), 438-439 (BPF).
16. Redifon Radio Diary, 1970, pp. 45–48, William Collins Sons & Co, 1969.
17. Matthaei, pp. 72–74.

Bibliography

• Mathaei, Young, Jones Microwave Filters, Impedance-Matching Networks, and Coupling Structures McGraw-Hill 1964 (1980 edition is ISBN   0-89006-099-1).
• For a simpler treatment of the analysis see,

• Ghosh, Smarajit, Network Theory: Analysis and Synthesis, Prentice Hall of India, pp. 564–569 2005 ISBN   81-203-2638-5.