In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple or star polygons.

In geometry, the pentagonal cupola is one of the Johnson solids. It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.
In geometry, the term semiregular polyhedron is used variously by different authors.

In geometry, the great dodecahedron is one of four Kepler–Poinsot polyhedrons. It is composed of 12 pentagonal faces, intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex.

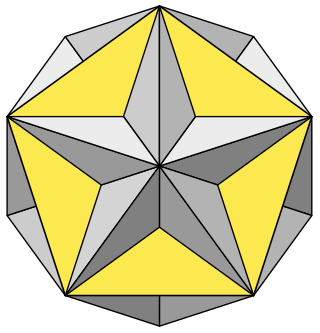
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.

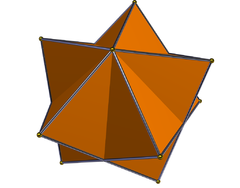
In geometry, the great stellated dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.

In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.

In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.

In geometry, the small ditrigonal icosidodecahedron (or small ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U30. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol a{5,3}, as an altered dodecahedron, and Coxeter diagram or .
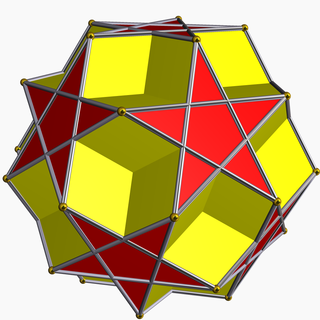
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

In geometry, the rhombidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U38. It has 54 faces (30 squares, 12 pentagons and 12 pentagrams), 120 edges and 60 vertices. It is given a Schläfli symbol t0,2{5⁄2,5}, and by the Wythoff construction this polyhedron can also be named a cantellated great dodecahedron.
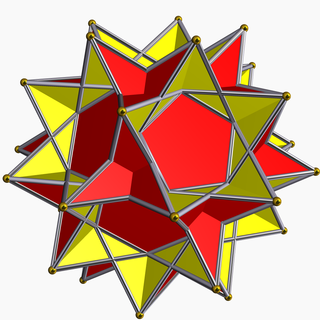
In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. It has 18 faces (12 pentagrams and 6 decagrams), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the nonconvex great rhombicosidodecahedron is a nonconvex uniform polyhedron, indexed as U67. It has 62 faces (20 triangles, 30 squares and 12 pentagrams), 120 edges, and 60 vertices. It is also called the quasirhombicosidodecahedron. It is given a Schläfli symbol rr{5⁄3,3}. Its vertex figure is a crossed quadrilateral.
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces.

In geometry, the density of a star polyhedron is a generalization of the concept of winding number from two dimensions to higher dimensions, representing the number of windings of the polyhedron around the center of symmetry of the polyhedron. It can be determined by passing a ray from the center to infinity, passing only through the facets of the polytope and not through any lower dimensional features, and counting how many facets it passes through. For polyhedra for which this count does not depend on the choice of the ray, and for which the central point is not itself on any facet, the density is given by this count of crossed facets.