
Plateau's laws describe the structure of soap films. These laws were formulated in the 19th century by the Belgian physicist Joseph Plateau from his experimental observations. Many patterns in nature are based on foams obeying these laws. [1]

Plateau's laws describe the structure of soap films. These laws were formulated in the 19th century by the Belgian physicist Joseph Plateau from his experimental observations. Many patterns in nature are based on foams obeying these laws. [1]
Plateau's laws describe the shape and configuration of soap films as follows: [2]
Configurations other than those of Plateau's laws are unstable, and the film will quickly tend to rearrange itself to conform to these laws. [3]
That these laws hold for minimal surfaces was proved mathematically by Jean Taylor using geometric measure theory. [4] [5]

A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.

A pattern is a regularity in the world, in human-made design, or in abstract ideas. As such, the elements of a pattern repeat in a predictable manner. A geometric pattern is a kind of pattern formed of geometric shapes and typically repeated like a wallpaper design.

Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects to float on a water surface without becoming even partly submerged.

In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis. It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.
Soap films are thin layers of liquid surrounded by air. For example, if two soap bubbles come into contact, they merge and a thin film is created in between. Thus, foams are composed of a network of films connected by Plateau borders. Soap films can be used as model systems for minimal surfaces, which are widely used in mathematics.
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who experimented with soap films. The problem is considered part of the calculus of variations. The existence and regularity problems are part of geometric measure theory.

A soap bubble is an extremely thin film of soap or detergent and water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds before bursting, either on their own or on contact with another object. They are often used for children's enjoyment, but they are also used in artistic performances. Assembling many bubbles results in foam.

In geometry, the triangular bipyramid is the hexahedron with six triangular faces, constructed by attaching two tetrahedra face-to-face. The same shape is also called the triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of triangular bipyramid are equilateral. It is an example of a deltahedron and of a Johnson solid.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.
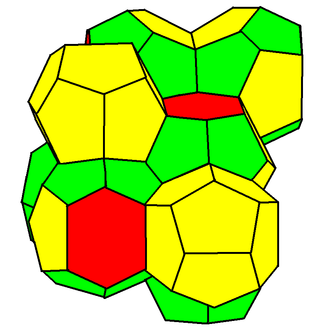
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure.

The capillary length or capillary constant is a length scaling factor that relates gravity and surface tension. It is a fundamental physical property that governs the behavior of menisci, and is found when body forces (gravity) and surface forces are in equilibrium.
In mathematics, geometric measure theory (GMT) is the study of geometric properties of sets through measure theory. It allows mathematicians to extend tools from differential geometry to a much larger class of surfaces that are not necessarily smooth.

Herbert Blaine Lawson, Jr. is a mathematician best known for his work in minimal surfaces, calibrated geometry, and algebraic cycles. He is currently a Distinguished Professor of Mathematics at Stony Brook University. He received his PhD from Stanford University in 1969 for work carried out under the supervision of Robert Osserman.

Reticulated foam is a very porous, low density solid foam. 'Reticulated' means like a net. Reticulated foams are extremely open foams i.e. there are few, if any, intact bubbles or cell windows. In contrast, the foam formed by soap bubbles is composed solely of intact bubbles. In a reticulated foam only the lineal boundaries where the bubbles meet remain.

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.

In the mathematical theory of minimal surfaces, the double bubble theorem states that the shape that encloses and separates two given volumes and has the minimum possible surface area is a standard double bubble: three spherical surfaces meeting at angles of 120° on a common circle. The double bubble theorem was formulated and thought to be true in the 19th century, and became a "serious focus of research" by 1989, but was not proven until 2002.

Jean Ellen Taylor is an American mathematician who is a professor emerita at Rutgers University and visiting faculty at the Courant Institute of Mathematical Sciences of New York University.

In mathematics, a minimal surface of revolution or minimum surface of revolution is a surface of revolution defined from two points in a half-plane, whose boundary is the axis of revolution of the surface. It is generated by a curve that lies in the half-plane and connects the two points; among all the surfaces that can be generated in this way, it is the one that minimizes the surface area. A basic problem in the calculus of variations is finding the curve between two points that produces this minimal surface of revolution.