In mathematics, a chain complex is an algebraic structure that consists of a sequence of abelian groups and a sequence of homomorphisms between consecutive groups such that the image of each homomorphism is included in the kernel of the next. Associated to a chain complex is its homology, which describes how the images are included in the kernels.
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted which records information about loops in a space. Intuitively, homotopy groups record information about the basic shape, or holes, of a topological space.
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics.
In mathematics, the Poincaré lemma gives a sufficient condition for a closed differential form to be exact. Precisely, it states that every closed p-form on an open ball in Rn is exact for p with 1 ≤ p ≤ n. The lemma was introduced by Henri Poincaré in 1886.
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. Every such cohomology theory is representable, as follows from Brown's representability theorem. This means that, given a cohomology theory
,
In mathematics, specifically algebraic topology, an Eilenberg–MacLane space is a topological space with a single nontrivial homotopy group.
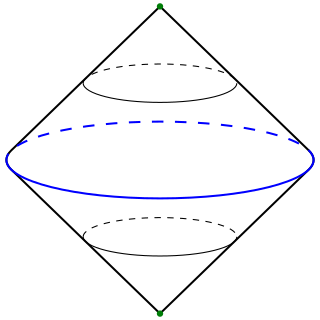
In topology, a branch of mathematics, the suspension of a topological space X is intuitively obtained by stretching X into a cylinder and then collapsing both end faces to points. One views X as "suspended" between these end points. The suspension of X is denoted by SX or susp(X).
In mathematics, a triangulated category is a category with the additional structure of a "translation functor" and a class of "exact triangles". Prominent examples are the derived category of an abelian category, as well as the stable homotopy category. The exact triangles generalize the short exact sequences in an abelian category, as well as fiber sequences and cofiber sequences in topology.

In mathematics, especially homotopy theory, the mapping cone is a construction in topology analogous to a quotient space and denoted . Alternatively, it is also called the homotopy cofiber and also notated . Its dual, a fibration, is called the mapping fiber. The mapping cone can be understood to be a mapping cylinder with the initial end of the cylinder collapsed to a point. Mapping cones are frequently applied in the homotopy theory of pointed spaces.
In mathematics, and specifically in the field of homotopy theory, the Freudenthal suspension theorem is the fundamental result leading to the concept of stabilization of homotopy groups and ultimately to stable homotopy theory. It explains the behavior of simultaneously taking suspensions and increasing the index of the homotopy groups of the space in question. It was proved in 1937 by Hans Freudenthal.
In mathematics, stable homotopy theory is the part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor. A founding result was the Freudenthal suspension theorem, which states that given any pointed space , the homotopy groups stabilize for sufficiently large. In particular, the homotopy groups of spheres stabilize for . For example,
In mathematics, specifically algebraic topology, there is a distinguished class of spectra called Eilenberg–Maclane spectra for any Abelian group pg 134. Note, this construction can be generalized to commutative rings as well from its underlying Abelian group. These are an important class of spectra because they model ordinary integral cohomology and cohomology with coefficients in an abelian group. In addition, they are a lift of the homological structure in the derived category of abelian groups in the homotopy category of spectra. In addition, these spectra can be used to construct resolutions of spectra, called Adams resolutions, which are used in the construction of the Adams spectral sequence.
In mathematics, the cotangent complex is a common generalisation of the cotangent sheaf, normal bundle and virtual tangent bundle of a map of geometric spaces such as manifolds or schemes. If is a morphism of geometric or algebraic objects, the corresponding cotangent complex can be thought of as a universal "linearization" of it, which serves to control the deformation theory of . It is constructed as an object in a certain derived category of sheaves on using the methods of homotopical algebra.
In mathematics, especially homotopy theory, the homotopy fiber is part of a construction that associates a fibration to an arbitrary continuous function of topological spaces . It acts as a homotopy theoretic kernel of a mapping of topological spaces due to the fact it yields a long exact sequence of homotopy groups
In the mathematical disciplines of algebraic topology and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram for a particular concept and reversing the direction of all arrows, much as in category theory with the idea of the opposite category. A significantly deeper form argues that the fact that the dual notion of a limit is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology. It is named after Beno Eckmann and Peter Hilton.
In homotopy theory, a branch of mathematics, the Barratt–Priddy theorem expresses a connection between the homology of the symmetric groups and mapping spaces of spheres. The theorem is also often stated as a relation between the sphere spectrum and the classifying spaces of the symmetric groups via Quillen's plus construction.
This is a glossary of properties and concepts in algebraic topology in mathematics.
The Whitehead product is a mathematical construction introduced in Whitehead (1941). It has been a useful tool in determining the properties of spaces. The mathematical notion of space includes every shape that exists in our 3-dimensional world such as curves, surfaces, and solid figures. Since spaces are often presented by formulas, it is usually not possible to visually determine their geometric properties. Some of these properties are connectedness, the number of holes the space has, the knottedness of the space, and so on. Spaces are then studied by assigning algebraic constructions to them. This is similar to what is done in high school analytic geometry whereby to certain curves in the plane are assigned equations. The most common algebraic constructions are groups. These are sets such that any two members of the set can be combined to yield a third member of the set. In homotopy theory, one assigns a group to each space X and positive integer p called the pth homotopy group of X. These groups have been studied extensively and give information about the properties of the space X. There are then operations among these groups which provide additional information about the spaces. This has been very important in the study of homotopy groups.
In mathematics, homotopy theory is a systematic study of situations in which maps can come with homotopies between them. It originated as a topic in algebraic topology, but nowadays is learned as an independent discipline.
In functional analysis, every C*-algebra is isomorphic to a subalgebra of the C*-algebra of bounded linear operators on some Hilbert space This article describes the spectral theory of closed normal subalgebras of . A subalgebra of is called normal if it is commutative and closed under the operation: for all , we have and that .















































